1.平均数指数变动的因素

指数因素分析法不仅可应用于总量指标的对比分析，还可应用于平均指标的对比分析。一般地，将两个不同时期的平均指标对比所形成的指数称为平均数指数。

在分组条件下，平均指标的变动往往取决于各组平均指标变动的影响和各组单位数在总体中的比重变动的影响。即：

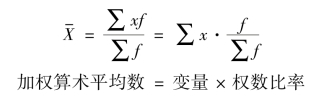
例如，影响某企业工人平均工资变动的原因是工人工资水平（x）的变动以及各组工人占工人总数比重（f／∑f）变动的影响。在对平均指标进行指数分析时，通常将各组单位数（f／∑f）占总数比重视为数量因素，将各组平均工资指标视为质量因素。与编制综合指数的原理相似，要分析工人工资水平（x）和各组工人占工人总数比重（f／∑f）变动对总平均工资的影响，就需引入同度量因素并将之固定。编制各组工人工资水平（x）的变动指数，应将作为同度量因素的各组工人占工人总数比重（f／∑f），即数量因素指标固定在“报告期”；编制各组工人占工人总数比重（f／∑f）变动的指数，应将作为同度量因素的各组工人工资水平（x），即质量因素指标固定在“基期”。推广到一般，可建立如下指数体系。

统计中把反映总平均数变动程度的指数称为质量因素。可变构成指数是指现象总体某种因素水平的变动。它是各组平均水平和总体结构变动两个因素相互作用的结果。公式为：

加权算术平均数的大小不仅取决于各组变量（x）的大小，还取决于各组权属比重（f／∑f）的大小。

为了消除总体中各组权数比重构成的影响，单纯反映各组变量值平均水平的变动，就需要权数比重固定在报告期计算平均数指数，这一指数称为固定构成指数。公式如下：

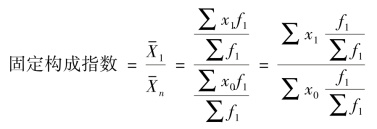
固定构成指数排除了各组权数比重构成的影响，单纯反映标志水平的变动程度。为了测定总体各组权数比重构成的影响，就需把标志值固定在报告期计算平均数指数，这一指数成为结构影响指数。计算公式如下：

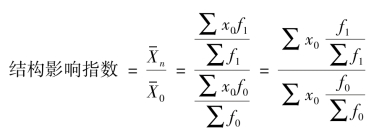
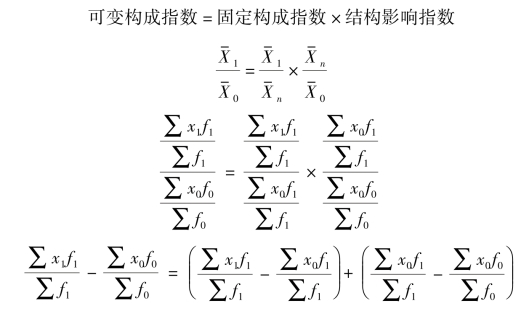
结构影响指数排除了各组标志水平（x）变动的影响，单纯反映各组权数比重构成的影响变动程度。由此可得平均数指数体系：

2.平均数指数变动的指数分析方法

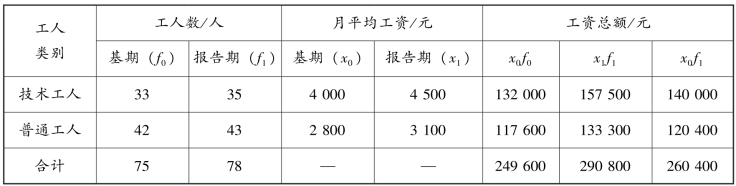
【例7-8】　某企业技术工人数及工资水平资料见表7-7。要求：试分析该企业工人总平均工资的变动情况及变动的原因（计算结果保留两位小数）。

表7-7　某企业技术工人数及工资水平

（1）分析该企业总平均工资的变动情况。平均工资可变构成指数如下所示：(www.daowen.com)

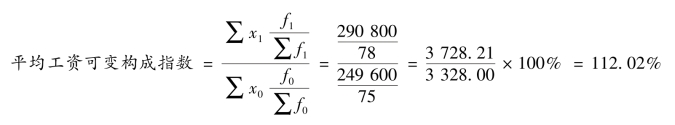
结果说明，该企业工人的总平均工资报告期比基期提高了12.03%，使工资总额增加了400.21 元。

为了进一步分析总平均工资变动的原因，就要分析各组平均工资和工人数结构对总平均工资总额变动的影响，即分别计算平均工资结构影响指数和平均工资固定构成指数。

（2）分析该企业各组平均工资变动对总平均工资的影响。平均工资结构影响指数如下所示：

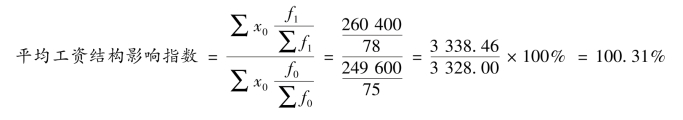
结果说明，该企业各级别工人数结构的变化使工资总额提高了0.31%，增加了10.46元（3 338.46 元-3 328.00 元）。

（3）分析该企业各等级工人数结构的变动对总平均工资的影响。平均工资固定构成指数如下所示：

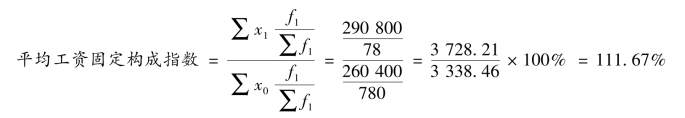
结果说明，由于该企业各等级工人数结构的变动，企业总平均工资提高了11.67%，增加了389.75 元（3 728.21 元-3 338.46 元）。

以上计算结果，可用指数体系表示如下：

平均工资可变构成指数＝平均工资结构影响指数×平均工资固定构成指数

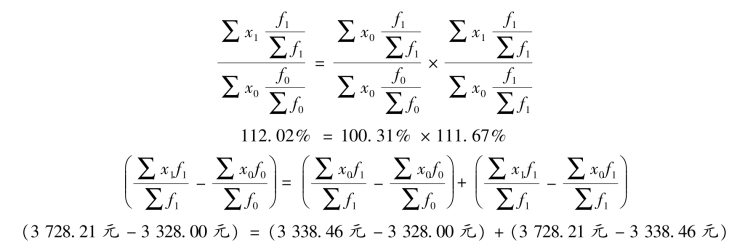
报告期与基期相比，平均工资提高了12.03%，增加了400.21 元。其中：由于工人结构变动（由普通工人向技术工人方向变动），工资总额提高了0.31%，总平均工资增加了10.46 元；由于各组工资水平提高了11.67%，总平均工资增加了389.75 元。

实际工作中，常用的平均数指数体系有：

3.平均数指数与平均指标指数的区别及联系

如前所述，平均数指数是对个体指数加权平均后求得的总指数，实际上仍是两个总量指标对比的结果。虽然采用了加权平均数指数和加权调和平均数指数的形式，但其计算结果在本质上仍是反映数量质量和质量指标的动态变动程度。它形成的指数体系和因素分析都针对总量指标。

平均指标指数是平均指标对比后形成的指数，其形成的指数体系和因素分析是针对平均指标的。它分析平均指标中由标志值和数量结构（不同于数量）变动引起的影响，是对平均指标做进一步深入分析的手段，由可变指数、结构影响指数和固定构成指数组成。

平均指标指数和平均数指数的共同之处在于两者都采用了加权平均的方法，平均数指数和综合指数的共同之处在于两者都采用了同度量因素。因此，从理论上讲，平均数指数在计算方法上综合了综合指数和平均数指数的特点，从而更能详细、深入地说明了指数方法和指标分析。实际工作中，往往把平均数指数划入总指数下的一个类别。