如前所述，平均数指数有两种：一是加权算术平均数指数；二是加权调和平均数指数。在每一种指数中，又由于所使用的权数不同，可再分为综合指数变形权数和固定权数两种。

1.加权算术平均数指数的编制

（1）用综合指数变形权数计算的加权算术平均数指数。

现以前述例子中的商品综合销售量和价格指数为例，说明算术平均数指数公式的形成过程。在7.2 中以基期价格和基期销量为同度量因素的销售量指数和价格指数公式分别为：

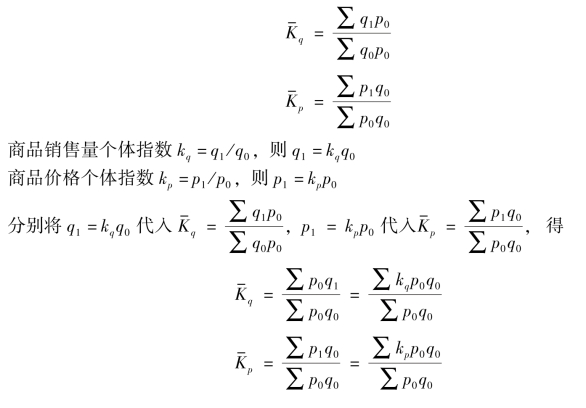
这就是以个体销售量指数（kq）和个体价格指数（kp）为变量，以基期销售额（p0q0）为权数的加权算术平均数指数的指数公式。由于这里的特定权数（p0q0）是综合指数的变形结果，虽然公式的形式与综合指数的形式不同，但是其经济内容及计算结果与综合指数完全一致，因此将其称为综合指数变形权数的加权算术平均数指数。

必须指出，只有将公式中的p0q0作为权数，加权算术平均数指数的形式才能转化为综合指数的形式，其变形关系如下：

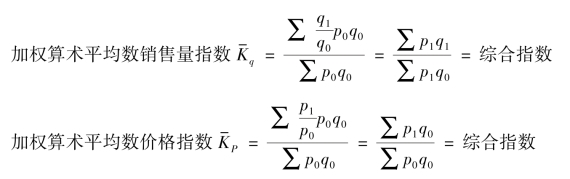
显然，若采用p0q0之外的任何其他权数，加权算术平均数指数都无法转化为综合指数。

【例7-4】　将【例7-2】 资料内容加以改变，假定仅知商品的销售量和基期的销售额数据，而没有对应的价格资料，则编制两种商品销售量总指数的方法见表7-3。

表7-3　某商店两种商品的销售资料

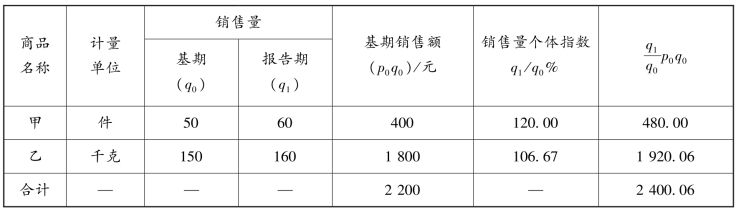
根据表中资料计算如下：

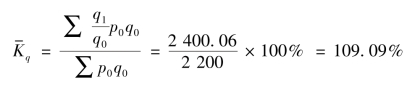
结果表明，两种商品销售量报告期比基期增长了9.09%，销售额增加了200.06 元（2 400.06-2 200）。这一结果与【例7-2】 中用拉氏物量指数公式的计算结果基本一致，只是因为在计算个体销售量指数时因无法整除而造成一定的误差。

（2）固定权数加权算术平均数指数。固定权数加权算术平均数指数，所用权数不是p0q0而是固定权数（W）。其公式为：

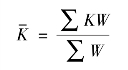
式中，代表固定权数加权算术平均数指数；W 为比重权数；K 为类指数或组指数。

固定权数加权算术平均数指数编制的一般步骤如下：

第一，根据研究目的分组或分类；

第二，在各组或类中选择代表品并计算个体组或类指数；

第三，分别确定代表品权数，小、中、大各组或类权数之和均为100；(www.daowen.com)

第四，进行加权算术平均，计算小、中、大各组或类指数和总指数。

【例7-5】　某省商贸统计资料见表7-4，求五类商品的总指数。

表7-4　某省商贸统计资料

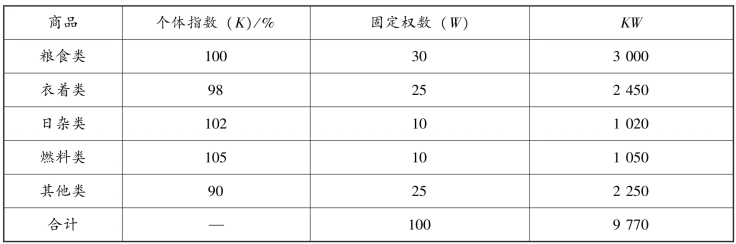
据表7-4 资料，五类商品的总指数为：

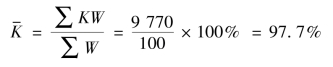
必须指出，计算固定权数加权算术平均数指数的关键在于选择代表品和确定权数。代表品应具有充分的代表性，其数目的多少应根据研究任务的需要确定。权数是以基期的实际资料为基础，结合报告期的变化情况确定的。例如，我国零售物价指数的编制，其权数一般是根据上年1—3 季度消费品实际零售额和第4 季度预计零售额，并参照本年度市场变化情况确定的。权数一律采用整数，每年确定一次，年内不变。

固定权数加权算术平均数指数在实际工作中应用比较广泛，像零售物价指数、消费者价格指数、工业生产指数等在我国及国外都采用这一编制方法。

2.加权调和平均数指数的编制

与加权算数平均数指数相对应，加权调和平均数指数也有两种加权方法。

（1）用综合指数变形权数计算的加权调和平均数指数。现仍以商品综合销售量和价格指数为例，说明调和平均数指数公式的形成过程。上节中，以报告期价格和报告期销售量为同度量因数的综合销售量和价格指数公式分别为：

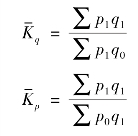
商品销售量个体指数为：

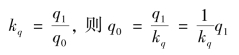
商品价格个体指数为：

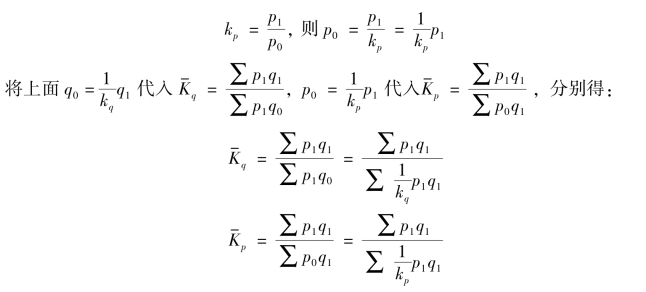
这就是以个体指数（kq、kp）为变量，以报告期销售额（p1q1）为权数的加权调和平均数指数公式。公式的形式虽然与综合指数公式形式不同，但是它的经济内容和计算结果与综合指数一致。

另外，上述公式中p1q1是特定的权数，因为只有用p1q1做权数，加权调和平均数指数的形式才能变成综合指数的形式。若用它以外的任何其他权数，加权调和平均数指数都不会等于综合指数，这恰恰是平均数指数的独立意义所在。

（2）固定权数加权调和平均数指数。若把上面公式中的权数p1q1改为某种固定的权数W，则加权调和平均数指数公式可写成：

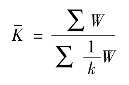
应该指出，这个公式实际应用较少，使用较多的是两种加权算术平均数指数。