测定季节变动的方法很多，这里仅介绍常用的同期平均法和趋势剔除法。

统计学上，测定现象季节变动的方法，主要是通过计算“季节比率”来完成的。所谓季节比率，又称季节指数，它是将现象各月（季）的发展水平与全期发展水平对比，得到的一种相对数，即它是以全期的总平均水平为基准（100%），用百分比的形式来反映各月（季）平均水平相对于总平均水平的高低程度。季节比率大（高），说明现象处于“旺”季，反之，则说明处于“淡”季。其计算公式为：

季节比率是用来刻画现象在一个年度内各月或季的典型季节特征，反映某一月份或季度的数值占全年平均数值大小的相对程度。显然，季节变动的程度是根据各季节指数与其平均数（100%）的偏差程度加以测定的。如果现象无季节变化，则季节比率等于100%；如果现象有明显的季节变化，则季节比率大于或小于100%。

必须指出，季节比率指标不能根据某一年度的资料来计算，因为个别年份的资料受偶然因素影响大，所以必须用三年以上各月或各季度的完整资料来计算。

1.同期平均法

同期平均法也称直接平均法或按月（季）平均法，它是测定季节变动最简便的方法，其特点是测定季节变动时，不考虑长期趋势的影响。该方法的基本思想：根据若干年（3 年以上）的资料数据，求出各年同月（季）的平均数与全年各月（季）的总平均数，然后将两者对比求出各月（季）的季节指数，以表明季节变动的程度。其具体步骤如下：

第一步：将各年同月（季）的完整数据资料排列整齐，并列表于同一栏。

第二步：将各年同月（季）数据加总，求出各月（季）平均数。

第三步：将全部月（季）数据加总，求出总的月（季）平均数。

第四步：根据公式求季节指数。

【例6-20】　某地区某种商品销售情况见表6-16，试用同期平均法计算季节比率，并做简要分析。

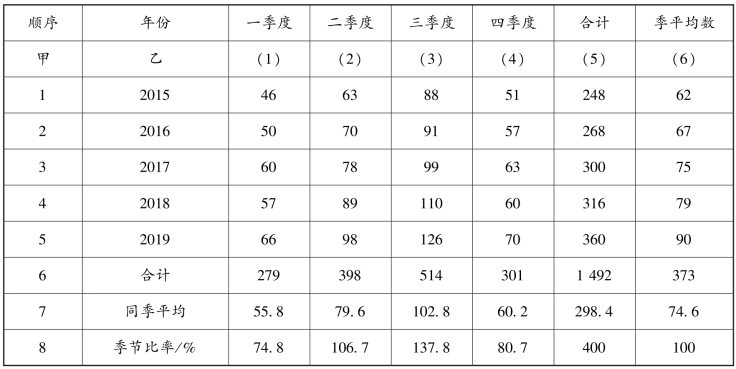
表6-16　某地区某种商品季节比率计算表

解：同期平均法的具体计算步骤如下分述。

第一步：将各年同月（季）的完整数据资料排列整齐，并列表于同一栏内。

第二步：计算同季（月）的合计数及平均数。见表6-16 中的第（6）行、第（7）行，计算年度的合计数及平均数，见表中的第（5）栏、第（6）栏。

第三步：计算全期季（月）平均数，本例5 年共20 个季度的平均数为74.6 万吨。

第四步：求季节比率，如：

第一季度季节比率：55.8 ÷74.6 ×100%＝74.8%

第二季度季节比率：79.6 ÷74.6 ×100%＝106.7%

其他依次类推，见表中的第（8）行。

四个季度的季节比率之和应等于400，如果不等，应进行调整。其具体方法：将400 除以四个季度季节比率之和，得到一个调整系数，然后，将此系数分别乘各季度原来的季节比率，即调整后的季节比率，它们之和等于400，本例恰好为400，不需调整。如果使用的是月份资料，则调整后季节比率之和应为1 200。

上例计算结果表明：该地区该种商品的销售，从第二季度开始上升，到第三季度进入旺季，随后，销售量下降进入淡季。显然，掌握了这些规律，商业流通部门就能心中有数，做到按时进货、适时供应，既节约资金，又可扩大销售；既可满足消费者的需要，又能增加企业盈利。

必须指出，根据季节变动规律，结合其他方法，还可进行预测。现根据表6-16 中的资料对该地区该种商品年及各季的销售量进行预测。具体步骤如下：

根据资料运用最小二乘法配合直线趋势方程，预测2020 年的销售量为380.6 万吨，则

平均每季销售量＝380.6/4＝95.15（万吨），故2020 年各季的预测值：

第一季度　95.15 ×0.748＝71.17（万吨）

第二季度　95.15 ×1.067＝101.53（万吨）

第三季度　95.15 ×1.378＝131.12（万吨）

第四季度　95.15 ×0.807＝76.78（万吨）

还必须指出，某些现象的季节变动并非是永恒的规律，随着科技的进步和人们生活习惯的改变，某些社会经济现象的季节变动会被削弱，甚至消失。例如，母鸡在冬季通常不产蛋，但在现代化的养鸡场，由于采用灯光代替太阳光来延长白昼，室内设有空调，采用专门的饲料配方增加营养，母鸡在冬天照样产蛋。(www.daowen.com)

另外，在实际中，季节变动的分析方法已被推广，凡在短期内，现象有周期性的规律变动，都可称为季节变动，当然，也可用这类方法进行测定，如一周内，哪一天公园的游客最多，商店的顾客哪一天最旺；一天中，哪些时段交通最拥堵等。

2.趋势剔除法

趋势剔除法是指在具有明显长期趋势变动的数列中，为了测定季节变动，必须先将长期趋势变动因素加以剔除的方法。其中，数列中的趋势值可采用移动平均法求得，也可采用最小二乘法求得。利用前者分析季节变动又称移动平均趋势剔除法，后者简称为趋势剔除法。

采用移动平均趋势剔除法分析季节变动时，假定长期趋势、季节变动、循环变动和不规则变动对时间数列的影响可以用乘法模型来反映，即Y＝T ＋S ＋C ＋I，同时假定各年度的不规则变动I 彼此独立。由于12 个月（或4 个季度）的移动平均数与季节变动周期（1 年）相同，通过移动平均可以完全消除季节变动和大部分不规则波动，而仅包含长期趋势和循环波动，结果为T×C。

然后，将原数列Y 除以移动平均趋势值T×C，所得百分比称为“季节变动和不规则变动相对数”或“移动平均百分比”，即：

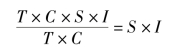
最后将各年同月（季）的移动平均百分比加以平均，即可消除不规则波动的影响，只剩下季节变动S。具体的步骤如下：

第一步：计算移动平均值（季度数据采用四项移动平均，月份数据采用十二项移动平均），并将其结果进行“中心化”处理，得到各期的长期趋势值T；

第二步：将各实际观察值Y 除以相应趋势值T，即

第三步：将S×I 重新按月（季）排列，求得同月（或同季）平均数，再将其除以总平均数，即得季节指数S。

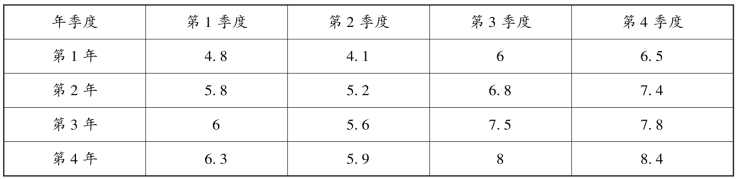
【例6-21】　按趋势剔除法计算表6-17 中某企业电视机销售量的季节指数。

表6-17　某企业四年的季度电视机销售量　单位：千台

解：首先，将用移动平均法求得长期趋势值T，然后利用公式计算出各季的包含循环变动和不规则变动的季节变动指数，见表6-18。

表6-18　电视机销售量季节指数计算表（一）

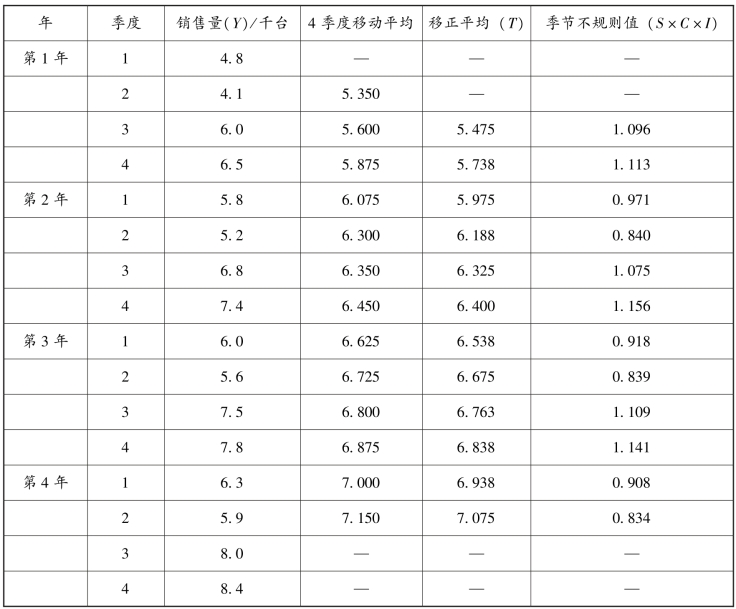
其次，利用同季平均的方法计算出电视机销售量时间数列的季节指数，消除循环变动和不规则变动。求得的季节指数分别为0.93、0.84、1.09、1.14，见表6-19。

表6-19　电视机销售量季节指数计算表（二）

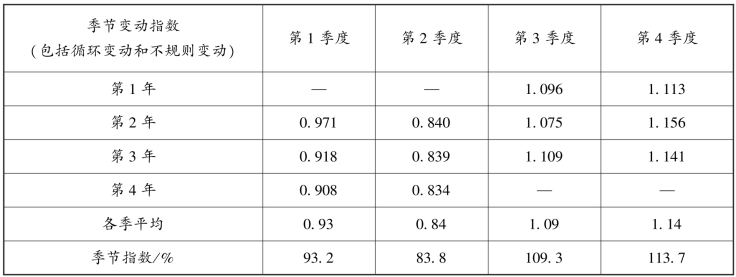
如果上一步求得的4 个季节指数的平均数不为1 或100%，则还要进行调整，即先求得4 个季节指数的总平均数，再用4 个季节指数与总平均数的比例，作为最后的季节指数。该例题中上一步计算的4 个季节指数的平均数已经为1，所以不需再进行调整。

相关知识图示

本章小结

社会经济现象总是随着时间的推移而变化，呈现动态性。统计对社会经济现象的研究，不仅要从静态上揭示研究现象在具体时间、地点、条件下的数量特征和数量关系，而且要从动态上反映其发展变化过程及其规律。统计对事物进行动态分析的基本方法就是编制时间数列，计算动态分析指标，对时间数列进行分解分析。因此，本章通过介绍时间数列的概念、种类和编制原则，以及如何对时间数列进行水平、速度、趋势分析，从而对若干个连续时期内的某一个经济变量进行测算。通过收集“过去”的时间里大量的数据资料，总结出规律性的结论，然后结合“目前”的客观现状，对“未来”做出判断和预测。

思考题

1.简述时期数列和时点数列的区别。

2.简述时间数列的编制原则。

3.简述“发展速度”和“平均发展速度”、“增长量”和“平均增长量”两对名词的区别。

即测即评

【注释】

[1]1 公顷＝10 000 平方米。