时间数列的长期趋势可以分为线性趋势和非线性趋势。当时间数列的长期趋势近似地呈现为直线，每期的增减数量大致相同时，则称时间数列具有线性趋势。当时间数列在各时期的变动随时间而不同，各时期的变化率或趋势线的斜率有明显变动但又有一定规律性时，现象的长期趋势就不再是线性趋势，而可能是非线性趋势。本部分重点介绍线性趋势模型法和半数平均法。

1.线性趋势模型法

线性趋势模型法也称直线配合法，是利用以时间t 为解释变量和以y 为被解释变量的线性回归方法，对原时间数列进行拟合，以消除其他成分变动影响，揭示时间数列的长期线性趋势。线性方程的一般形式为

式中，yc为时间数列的趋势值；t 为时间变量；a 为趋势线在y 轴上的截距；b 为趋势线的斜率，表示时间t 增加或减少，即变动一个单位时趋势值yc的平均变动数量。通常利用最小二乘法估计线性趋势方程的参数。

最小二乘法又称最小平方法，其基本思想是：∑（y- yc）2＝最小值。

将yc＝a ＋bt，代入∑（y- yc）2，令Q＝∑（y- yc）2＝∑（y- a- bt）2，根据微分求极值的原理，分别对a 和b 求偏导，令其为零。得：

则可得直线回归方程：yc＝a ＋bt。

现以表6-14 中，某地区2010—2019 年的粮食产量资料为例来计算。

【例6-18】　依资料计算该地区粮食产量历年的趋势值yc（表6-14）。

表6-14　某地区2010—2019 年的粮食产量资料（最小二乘法计算表）

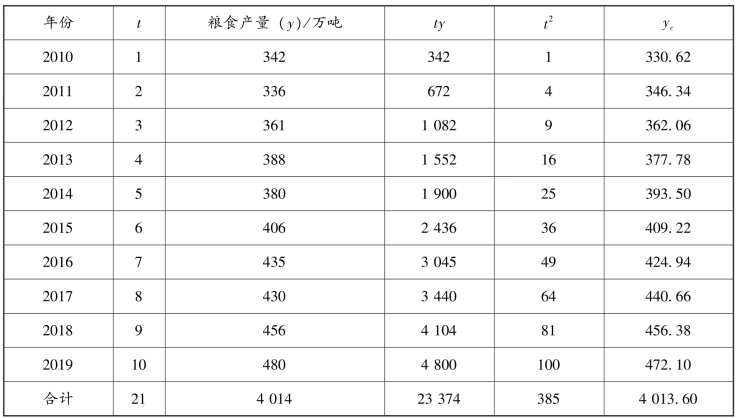
将表6-14 中合计栏的数据，代入上列标准方程得：

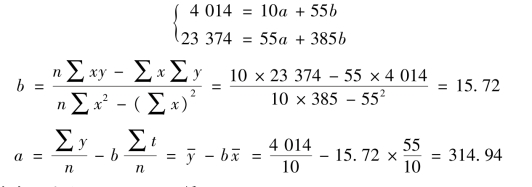
将a，b 值代入方程yc＝a ＋bt，得：

将时间顺序1，2，3，… ，10 分别代入该直线趋势方程的t，即分别得该地区粮食产量历年的趋势值（见表6-14 中的yc栏数列）。(www.daowen.com)

2.半数平均法

直线趋势方程的一般式为：

式中，各符号的含义同前。

设y 为原数列的实际值；n 为数据项数。根据半数平均法的要求，实际观察值y 与趋势值yc的离差之和为零，即∑（y- yc）＝0。将yc＝a ＋bt 代入得：

即∑y-∑a-∑bt＝0

用n 除上式后得：

【例6-19】　现仍以表6-14 中某地区2010—2019 年的粮食产量资料为例，说明趋势方程建立的方法。

第一步：将原数列均分为两半，如果原数列为奇数项，则删除最初一期数值即可。

第二步：用时间顺序t，即1，2，3，… ，10 分别代表各年份（表6-15）。

表6-15　某地区2010—2019 年的粮食产量资料（半数平均法计算表）

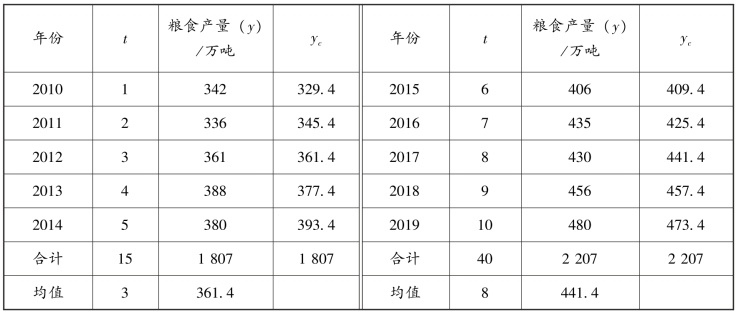
第三步：分别计算这两半数列时间变量t 的均值和现象实际水平y 的均值（表6-15 中已列出）。则有：

第五步：解此方程得b＝16，a＝313.4，代入方程yc＝a ＋bt，即得所求的直线趋势方程yc＝313.4 ＋16t。

该直线趋势方程表明：当t＝0 时，趋势值为313.4，即该直线趋势方程的起点为313.4万吨，每增加一年，产量平均增长16 万吨。将时间顺序1，2，3，…，10 分别代入t，可分别得到各年粮食产量的趋势值。