1.间距扩大法

在介绍移动平均法之前，我们先来介绍间（时）距扩大法。间距扩大法是测定长期趋势最原始、最简单的方法。它是将原来时间数列中较小时距单位的若干个数据加以合并，得到较大时距单位的数据。当原始时间数列中各指标数值上下波动，使得现象变化规律表现不明显时，可通过扩大数列时间间隔，使得较小间距数据所受到的偶然因素的影响相互抵消，以反映现象发展的长期趋势。

【例6-16】　根据表6-9 的数据，用间距扩大法分析某商场商品销售额的长期趋势。

表6-9　某商场某年商品销售额资料　单位：万元

解：将以月为时距的时间数列合并为以季为时间距离的时间数列，见表6-10。由原时间数列，并不能很好地观察出长期趋势，在扩大间距后的新时间数列中，可以明显地看出商场的销售量呈现增长的趋势。

表6-10　间距扩大法计算某商场某年商品销售额的长期趋势　单位：万元

间距扩大法的优点是简便直观。但是它的缺点也很突出，扩大间距后形成的新时间数列包含的数据减少，信息量大量流失，不便于做进一步分析。另外，间距究竟扩大到何种程度为宜，应以现象和原时间数列的特点来定，以能明显反映现象的发展趋势为准。

2.序时平均法

由于时点数列各期水平相加无实际意义，因此，时点数列不能直接用间距扩大法，需利用序时平均法消除偶然因素的影响，以反映现象的变化趋势。例如，表6-9 中的时点数列的变化趋势不够明显，采用序时平均法消除偶然因素影响后，其变动趋势则较明显（表6-11）。

表6-11　某商场2019 年各月月末售货员人数资料　单位：人

由于以月为时点间隔且间隔相等，则可采用首末折半法，计算各季度的序时平均数并填入表6-12。

表6-12　某商场2019 年季度平均售货员人数资料　单位：人

显然，经过平均后各季售货员人数递增的趋势就很明显。时期数列也可采用此法。

3.移动平均法(www.daowen.com)

移动平均法是对间距扩大法的一种改良。它是采取逐期递推移动的方法对原数列按一定间距扩大，得到一系列扩大间距的平均数。其原理与间距扩大法类似，通过扩大间距来消除时间数列中的不规则变动和其他变动的影响，揭示出时间数列的长期趋势。较间距扩大法的优点在于，移动平均法可以保留更多的数据信息，对原时间数列的波动起一定的修匀作用。移动平均法的具体步骤如下：

第一步：扩大原时间数列的时间间隔，选定一定的间距项数N。

第二步：采用递次移动的方法对原数列递次移动N 项计算一系列序时平均数。

【例6-17】　某地区2009—2019 年粮食产量资料见表6-13，请用移动平均法修匀该地区的粮食产量数据。

表6-13　某地区2009—2019 年粮食产量资料　单位：万吨

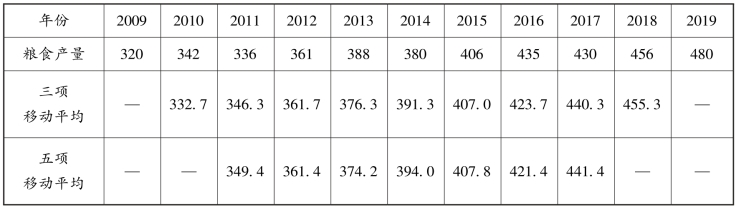
解：

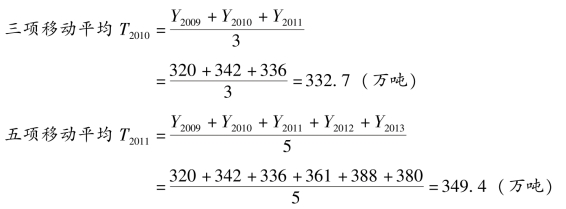
其他各年数字以此类推，所得移动平均数，写在间距最中央的那一年的位置上即可。

显然，五项移动平均法与三项移动平均法相同，只是间距更大些。当然，也可做七项移动平均、九项移动平均等。那么，究竟做几项移动平均，要视数列和现象的具体情况而定。

一般来说，间距项数越多，移动平均时间数列的修匀程度越大，而所得新的时间数列的项数则越少。即新时间数列项数＝原时间数列项数-时距项数＋1，如上例三项移动平均的项数＝11-3 ＋1＝9。

必须指出，实际工作中也可做四项、六项、八项等偶数移动平均，即对原数列进行间距为偶数项移动平均时，对所得移动平均数应该再做一次二项移动平均，以移正其位置。一般来说，如原数列为年度资料时，间距定为三项、五项或七项为宜；原数列为月度或季度资料时，间距定为四项或十二项为宜。

从上例不难看出，移动平均法有以下特点。

（1）间距项数N 越大，对时间数列的修匀效果越强。如三项移动平均的波动较原数列明显削弱了，但是仍存在一些小波动，而五项移动平均进一步削弱了波动，时间数列呈现出持续上升的长期趋势。

（2）移动平均时距项数N 为奇数时，一般只需一次移动平均，其移动平均值作为移动平均项数的中间一期的趋势代表值；当移动平均时距项数N 为偶数时，移动平均值代表的是偶数项的中间位置，无法对正某一时期，所以需进行一次相邻两项平均值的再次移动平均，如此才能使得平均值对正某一时期。第二次移动平均称为移正平均，也称中心化的移动平均数。

（3）N 的选择要考虑周期性波动的周期长短，平均间距N 应和周期长度一致。当时间数列包含季节变动时，移动平均时距项数N 应与季节变动长度一致，一般为4 个季度或12个月。

（4）移动平均以后，其数列的项数较原序列减少。当原数列的项数为N 时，移动n 项，那么，移动后新数列项数为N-（n-1）＝N-n ＋1 项，比原数列项数减少（n-1）项。

（5）虽然移动项数越多，修匀效果越强，但是移动项数过多，必将造成数据丢失增多的结果。因此，实际中，必须综合考虑以上特点来选择适宜的移动平均间距项数。