平均发展速度是某种现象各期环比发展速度的平均数，它说明该现象在一个较长时期内，发展速度变化的平均程度，即平均单位时间发展变化的程度。

平均增长速度是某种现象各期环比增长速度的平均数，它说明该现象在一个较长时期内，平均单位时间增长的程度。平均增长速度虽然是各期环比增长速度的平均数，但它不能直接由各期环比增长速度计算，而是由平均发展速度减1 或减100%求得。平均增长速度有正负之分，正值表示平均增长的程度，负值表示平均下降的程度。

在我国，根据被研究现象的特点和统计分析的目的不同，平均发展速度的计算有水平法和累计法两种。水平法又称几何平均法，累计法又称代数平均法或方程法。

一般地，在正常情况下，两种方法计算的平均每年增长速度比较接近。但在经济发展不平衡、出现大起大落时，两种方法计算的结果差别则较大。在我国的实际统计工作中，除固定资产投资、造林面积等采用“累计法”计算外，其余多用“水平法”计算。

1.水平法

水平法又称几何平均法，是以时间数列最后一年的发展水平同基期水平对比来计算平均每年增长（或下降）速度。一般地，凡用年发展水平表现其规模的现象，如产品产量、产值、商品销售额和职工人数等，适合用水平法计算平均发展速度。计算公式如下：

式中，代表平均发展速度；X1，X2，X3，…，Xn为各期环比发展速度；R 为总速度；n为各期环比发展速度指标的项数；m 为翻番数。

平均增长速度和平均发展速度的关系是：

【例6-11】　按可比价格计算，某地区人均生产总值1999 年为379 元，2019 年为6 392 元，试计算该地区2000—2019 年生产总值的平均发展速度和平均增长速度。

解：∵a0＝379，an＝6 392，n＝20，则：

两边取对数得：

查反对数表得＝1.151 7，即平均发展速度为115.17%，平均增长速度为11.17%。

应指出，上述计算只是为了从理论上说明，实际中是运用多功能计算器计算，计算方法从略。

【例6-12】　某地区2014—2019 年甲产品的单位成本及环比发展速度见表6-8，试计算2014—2019 年的平均发展速度。

表6-8　某地区2014—2019 年甲产品的单位成本及环比发展速度

解：根据表中资料可知，n＝5 时各年环比发展速度xi（具体数值见表），则：

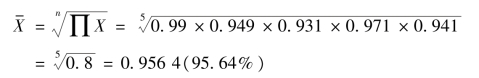
所以，平均增长速度为95.64%-100%＝-4.36%，即平均下降4.36%。

【例6-13】　某地区2010 年税收总额为12 亿元，计划到2030 年较2010 年翻两番，试求平均增长速度是多少。

解：∵m＝2，n＝20，则代入公式得：

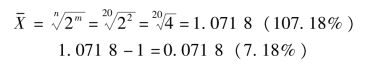
所以，平均增长速度为107.18%-100%＝7.18%，即平均增长速度为7.18%。(www.daowen.com)

需要指出，在统计实践中，为提高工作效率，学者们根据几何级数原理编制了“水平法平均增长速度查对表”，该表分为平均增长和平均下降两部分，只要知道某一段时期的定基发展速度R，而后知道该段时间的间隔年数或环比发展速度的个数n，则可查表直接得到平均增长速度或下降速度，然后将之加100%即得平均发展速度。应注意，查表前，应先判断现象是增长或下降，凡R ＞100%，属增长，应查增长部分表；反之，应在下降部分查表。

若某种现象在一定时期内的各期环比发展（或增长）速度大体相等，则可据此进行预测。

2.累计法

累计法又称代数平均法或高次方程法，是以时间数列内各年发展水平的总和同基期水平对比来计算平均每年的增长（或下降）速度，即时间数列中各年发展水平的总和等于全期的总水平，各期发展水平是基期水平与各该期定基发展速度的乘积。一般地，对用若干年累计数表现其规模的现象，适宜于采用累计法计算平均发展速度。

按这种方法计算平均发展速度的数理依据是：从现象的最初水平a0出发，每年若都按平均发展速度发展，所得各年水平之和，等于现象各报告年实际发展水平之和。

现象各报告年实际发展水平之和为：

解此高次方程所得正根，即所求的平均发展速度。显然，解此方程是非常麻烦的，通常是借助事先编制的“累计法平均增长速度查对表”解决。该表也分为平均增长和平均下降两部分，只要掌握现象某一段时间的总发展速度（即各年发展水平总和与基期水平之比，通常以M 且用百分数表示，M＝（∑a／a0）×100%），以及该段时间的间隔年数n，就可查表直接得到平均增长速度或平均下降速度。同样，在查表前，必须判断现象是增长还是下降。凡为增长，在增长部分查表；反之，在下降部分查表。

【例6-14】　某地区固定资产投资额2015 年为4 679 万元（a0），2016—2019 年每年分别为5 220 万元、5 628 万元、5 943 万元和6 124 万元，共计22 915 万元（∑a）。试用累计法求此期间年平均增长速度和年平均发展速度。

解：∵M＝∑a／a0＝（22 915／4 679）× 100%＝489.74%，n＝4，M／n＝122.43% ＞100%，属增长，故应在增长部分查表。

从n＝4（年）看，总发展速度489.74%是在489.00%和490.18%之间，按比例计算得

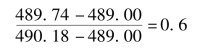
则有：

∴平均增长速度为8.26%，平均发展速度为108.26%。

【例6-15】　某地区造林面积2014 年为200 公顷^[1]（a0），2015—2019 年隔年分别为198 万公顷、188 万公顷、175 万公顷、170 万公顷和160 万公顷，共计891 万公顷（∑a）。试用累计法求此期间年平均增长速度和年平均发展速度。

解：∵M＝∑a／a0＝（819／200）×100%＝445.5%，n＝5，M／n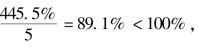＝属下降，故应在下降部分查表。

从n＝5 年看，总发展速度445.5%是在445.81%与444.45%之间，按比例计算得：

则有：

∴平均下降速度为3.82%，平均发展速度为96.18%。

必须指出，水平法和累计法不同，水平法侧重于考察最末一期（年）的发展水平，按这种方法确定的平均发展速度，推算的最后一年发展水平，等于最末一期（年）的实际发展水平；推算的最末一期（年）的定基发展速度和根据实际资料计算的最末一期（年）定基发展速度是一致的。累计法侧重考察全期的总和水平，按这种方法确定的平均发展速度，推算的全期的总和水平与各期实际水平总数是一致的；推算的各部分定基发展速度的总和与根据实际资料计算的定基发展速度的总和是一致的。

另外，平均发展速度指标是现象在一个较长时期内，各年环比发展速度的平均数，用以说明现象在该时期内逐年发展变化的一般程度，它抽象了各年的实际变化程度。因此，计算和应用平均发展速度指标应注意以下两个问题：

第一，要结合具体情况确定基期。因为基期水平是起点、标准，它对研究目的的实现具有重要意义，对平均发展速度也是有影响的。例如，如果研究某五年计划期内的平均发展速度，应以该五年计划的前一年为基期；若研究我国改革开放以来的平均发展速度，就应以1978 年为基期；若研究中华人民共和国成立以来我国的平均发展速度，则以1949 年为基期更恰当。

第二，应计算分段平均发展速度来补充全期的平均发展速度。因为在一个较长的历史时期，现象的变化各阶段各有特点，即有快有慢、有增有减，为更具体地反映情况，必须用分段平均发展速度来补充说明全期的平均发展速度。