1.发展速度

发展速度是反映社会经济现象发展快慢的相对指标。用两个不同时期的发展水平相对比而求得。计算公式如下：

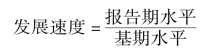
发展速度一般用百分比来表示，当比值较大时，也可用倍数和翻番数表示，它说明现象报告期水平为基期水平的百分之几、若干倍或翻几番。当它大于100%（或1）时，表明现象在增长，当它小于100%（或1）时，则表明现象在下降。

由于采用的基期不同，可将发展速度分为环比发展速度和定基发展速度。环比发展速度是报告期水平与前一期水平之比，反映现象的逐期发展程度。定基发展速度是报告期水平与某一固定基期水平（通常是最初水平）之比，它表明报告期水平为某一固定基期水平的百分之几、若干倍或翻几番，反映现象在较长一段时间内的发展程度，故也称为总发展速度。

这两个增长速度虽然计算基期和说明的问题不同，但它们之间存在一定的换算关系，即同一动态数列，各期环比发展速度的连乘积，等于相应的定基发展速度；相邻两个时期的定基发展速度之商等于相应时期的环比发展速度。

设基期水平为a0，各报告期水平为ai（i＝1，2，3，…，n），则：

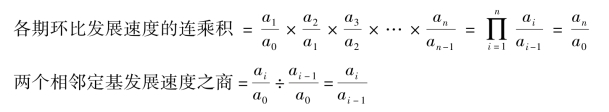
【例6-8】　某公司2011—2019 年销售收入及其发展速度见表6-6。

表6-6　某公司2011—2019 年销售收入及其发展速度

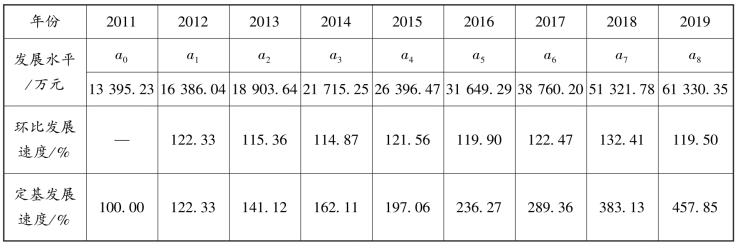
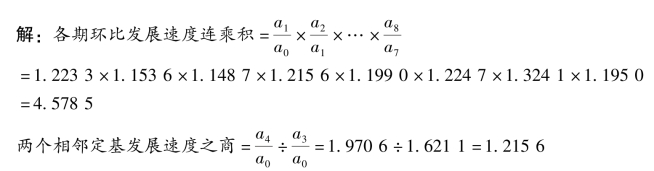
2.增长速度

增长速度是表明社会经济现象增长程度的相对指标。它可以根据某一现象报告期增长量与基期发展水平对比求得，也可以根据发展速度减1（或100%）求得。公式如下：

增长速度也有正负之分，正值表示增长的程度，负值表示下降的程度。

增长速度由于采用的基期不同，也有环比增长速度和定基增长速度之分。环比增长速度是将基期定为报告期的前一期，用报告期的增长量与前一期的发展水平对比而得，反映现象的逐期增长程度。定基增长速度是将基期固定为某一期，用报告期的增长量与固定基期的发展水平对比而得，反映现象在较长一段时间内的增长程度。

(www.daowen.com)

【例6-9】　某企业近几年产量不断增长。已知2015 年比2014 年增长20%，2016 年比2015 年增长50%，2017 年比2016 年增长25%，2018 年比2017 年增长15%，2019 年比2014 年增长132.5%，计算表6-7 中的空缺数字。

表6-7　某企业2015—2019 年产量增长速度

解：根据环比发展速度和定基发展速度之间存在的数量关系，增长速度可以根据发展速度求得，所以计算增长速度时先计算各期的发展速度，然后再通过“增长速度＝发展速度-1”的关系式，计算出各增长速度。

2015 年定基增长速度＝20%

2016 年环比增长速度＝

2017 年定基增长速度＝｛［（1 ＋20%）×（1 ＋20%）×（1 ＋25%）］-1｝ ×100%＝87.75%

2018 年定基增长速度＝［（1 ＋87.5%）×（1 ＋15%）-1］×100%＝115.6%

2019 年环比增长速度＝｛［（1 ＋132.5%）÷（1 ＋115.6%）］-1｝ ×100%＝7.84%

必须指出，环比增长速度与定基增长速度无直接的换算关系。如果由一个环比增长速度数列求其定基增长速度数列，需先将各期环比增长速度换算成各期环比发展速度，再将它们连乘，求得各期的定基发展速度，最后，将各期定基发展速度分别减1 或100%，可得各期的定基增长速度。相反，若知现象各期的定基增长速度，求各期的环比增长速度，也要经过一定的变换计算求得。

另外，在统计实践中，为消除季节变动的影响，还需使用年距发展速度和年距增长速度。年距发展速度是现象报告年某月（季）的水平与其上年同月（季）水平之比。年距增长速度是现象报告年某月（季）的年距增长量与上年同月（季）现象的水平之比，或者用年距发展速度减1 或减100%求得。

为进一步对比分析现象的增长情况，实践中还需计算“增长1%的绝对值”指标。计算公式为

【例6-10】　甲、乙两厂，报告期甲厂利税额的环比增长速度为10%，增长量为5 万元；乙厂为5%，增长量为7.5 万元。请判断两厂谁的效益好、贡献大。

解：若单从增长速度看，甲厂的增长速度是乙厂的两倍，似乎甲厂好于乙厂。但是联系两厂报告期的逐期增长量，计算增长1%的绝对值后，则会得出相反的结论。

甲厂：增长1%的绝对值＝7.5/5＝1.5（万元）

乙厂：增长1%的绝对值＝5/10＝0.5（万元）

显然，甲厂的效益好于乙厂。增长1% 的绝对值的实质就是现象前期水平（ai-1）的1%。