1.发展水平
在时间数列中,各项具体的指标数值称为发展水平,即该指标反映的社会经济现象在所属时间的发展水平。在表6-2 中,2007 年的国内生产总值为270 884 亿元,即2007 年的GDP 发展水平,2017 年年末人口数为139 008 万人,即2017 年的人口发展水平。在一个时间数列中,各时间上的发展水平按时间顺序可以记为y0,y1,y2,…,yn-1,yn。在对各个时间的发展水平进行比较时,把作为比较基础的那个时间称为基期,相对应的发展水平称为基期水平;把所研究考察的那个时间称为报告期,相对应的发展水平称为报告期水平。基期和报告期将根据研究的需要而定。
2.平均发展水平
平均发展水平是指将不同时期的发展水平加以平均而得的平均数,又称序时平均数或动态平均数。它与前面讲过的一般平均数既有相同的一面,也有明显的区别。相同点:两者都是将现象的个别数量差异抽象化,概括地反映现象的一般水平。不同点有二:一是平均发展水平平均的是现象在不同时间上指标数值的差别,是从动态上说明现象的一般水平,是根据时间数列计算的;而平均指标平均的是现象在同一个时间上的数量差别,是从静态上说明现象的一般水平,是根据变量数列计算的。二是平均发展水平是对同一现象不同时间上的数值差异的抽象化,而一般平均数是对同一时间总体某一数量标志值的抽象化。另外,平均发展水平还可以解决时间数列中某些可比性问题。例如,各月的日历天数不同,这会影响企业总产值的大小,但如果以计算出各月的每日平均总产值指标来计算对比,就具有可比性,更能反映总产值的发展情况。
计算平均发展水平的方法,依时间数列指标的性质而定。既可根据绝对数时间数列计算,也可根据相对数或平均数时间数列计算。而根据绝对数时间数列计算序时平均数的方法是最基本的方法。
(1)由绝对数时间数列计算序时平均数。由于绝对数时间数列分为时期数列和时点数列,两者各具不同的性质,因此计算序时平均数的方法也不同。
①由时期数列计算序时平均数。由于数列中的各项指标数值相加等于全部时期的总量,因此可采用简单算术平均数方法计算。公式为:

式中,![]() 代表平均发展水平;a1,a2,…,an为各期发展水平;n 为数列水平项数。
代表平均发展水平;a1,a2,…,an为各期发展水平;n 为数列水平项数。
【例6-1】 根据表6-2 第(2)列的数据计算2007—2017 年我国的年均国内生产总值。
解:将2007—2017 年的国内生产总值代入式(6-1),即:
2007—2017 年的平均国内生产总值为
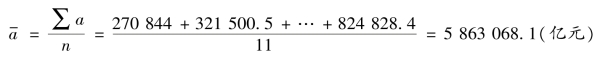
②由时点数列计算序时平均数。如果利用式(6-1)计算时点数列的序时平均数,理论上要求掌握现象在每一时点上的数据。然而,由于我们不可能统计出现象发展变化过程中每一时点上的数值,只能每隔一段时间统计其余额。所以,根据时点数列计算的序时平均数是假定在某一时间间隔内现象的增减变动比较均匀或波动不大的前提下推算出的近似值。时点数列按其间隔的表现形式不同,可分为间隔相等的连续时点数列、间隔不等的连续时点数列、间隔相等的间断时点数列、间隔不等的间断时点数列四种。
a.由间隔相等的连续时点数列求序时平均数。这种数列是以日为间隔编制的,其特点是间隔都为一天,逐日记录资料并将考察期内资料按日加以排列。可用简单算术平均法求解序时平均数。公式同式(6-1)。
例如,若已知某企业某月每天的工人数,要计算该月每天平均工人数,则可将每天的工人数相加,除以该月的日历天数即可。
b.由间隔不等的连续时点数列求序时平均数。此数列的特点是考察期内被研究现象并不是逐日发生变动统计的,而是隔一段时间变动后统计一次,并根据变动情况进行分组,以不相等的时点间隔数为权数,采用加权算术平均法求序时平均数。
【例6-2】 某企业2020 年6 月份某成品的库存量资料见表6-3,计算该企业6 月份某成品的平均库存量。
表6-3 某企业2020 年6 月份某成品的库存量

解:该企业6 月份某成品的平均库存量为:
![]()
由此推广到一般公式为:(https://www.daowen.com)
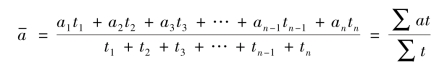
式中,a1,a2,…,an为各期发展水平;t1,t2,…,tn为与现象各期水平相对应的时间距离;其他符号同式(6-1)。
c.由间隔相等的间断时点数列求序时平均数。在实际工作中,许多统计指标都不是逐日登记的,而是每隔相同的时间段登记一次,这就组成了间隔相等的间断时点数列。对于这种间隔相等的时点数列,应采用“首末折半法”求序时平均数,公式如下:
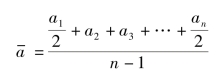
式中,n 为各时点指标数值个数;n-1 为间隔数;其他符号同式(6-1)。
必须指出,这个公式基于一个假设,即假设每个时点间隔内的现象数量的变化是均匀的。
【例6-3】 根据表6-2 第(3)列的数据,计算2008—2017 年我国年平均人口数。
解:首先要考虑的是首项应该是哪一年的数据,显然,首项不是2008 年年末人口数,而是2007 年年末人口数。2008 年的人口变化从2007 年年末开始到2008 年年末,所以2026年年末人口数不能作为2008 年人口的代表值,将2007 年年末的人口数看成2008 年年初的人口数,2008 年的年平均人口就是年初和年末人口的简单平均数。
类似地可以计算2009—2017 年的各年平均人口数,计算结果如表6-2 中第(4)列所示。然后再对各年平均人口数进行算术平均,求出2008—2017 年的年平均人口数。即:
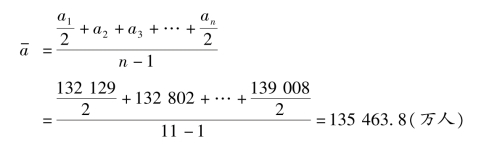
d.由间隔不等的间断时点数列求序时平均数。根据间隔不等的间断时点数列求序时平均数,其思路与间隔相等的时点数列相同,同样假设每个时间间隔之间的数量变化是均匀的。由于时点间隔不等,需要以时点间隔长度为权数,用加权序时平均法来求序时平均数。公式如下:

式中,t1,t2,…,tn为与现象各期水平相对应的时间距离;其他符号同式(6-1)。
【例6-4】 某农场某年的生猪存栏数见表6-4,计算该农场的年平均生猪存栏数。
表6-4 某农场某年的生猪存栏数

解:该农场的年平均生猪存栏数为:
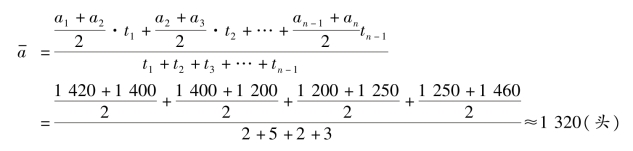
(2)由相对数或平均数时间数列求序时平均数。由于相对数和平均数是由绝对数派生出来的,因此,相对数或平均数时间数列也是派生数列,即其中各项指标都是由两个绝对数对比计算出来的。所以在计算绝对数和平均数的序时平均数时,就不能直接计算其各项指标的平均数,而是要分别先计算出两个绝对数的平均水平,然后进行对比即可。

【例6-5】 根据表6-2 的数据计算2008—2017 年我国年平均的人均GDP 值。
解:根据资料的性质,不能对人均GDP 的各项发展水平直接进行算术平均,而是先计算国内生产总值的平均发展水平和年均人口数,再对比得到年人均GDP 值。具体计算如下:
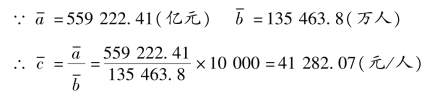
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






