1.样本容量的含义

样本容量就是抽样数目。根据大数定理，在抽样调查中样本容量越多，样本对总体的代表性越大，抽样误差越小；样本容量减少，抽样误差就要增大。同时，样本容量越多，抽样调查的费用也越高，而且会影响抽样调查的时效性。因此，确定样本容量时，应在保证满足抽样调查对数据的估计精确度和概率把握程度下，尽量缩小样本容量，即必要样本容量。

2.确定必要样本容量的意义

确定样本容量是抽样方案设计的一个重要内容。必要样本容量是指为了完成抽样调查任务，满足抽样调查的各项要求而科学计算的需要抽取的样本单位数，即样本单位数“n”的具体数值。

确定样本容量既要满足抽样估计的精确度要求，也要尽可能节省人力、物力，减少抽样调查的费用。为了提高抽样估计精确度，样本容量越多越好，根据大数定律，抽样单位数越多，样本的代表性越大，抽样误差越小，抽样推断越可靠。但抽取单位数过多，就失去了抽样推断的意义；从节省角度看，样本容量也是越少越好。

科学地确定必要样本容量是一个十分重要的问题。实践中要做到，在抽样实施之前，必须根据抽样原理和要求，科学、合理地确定样本容量，在满足抽样误差要求的前提下，使样本容量尽可能少；或在限定调查费用的条件下，使样本容量尽可能多。或者说，抽样误差不超过给定的允许范围至少应抽取的样本单位数目。通常情况下，要根据规定的允许误差来确定必要的样本容量。

3.必要样本容量的确定

简单随机抽样方式下，必要样本容量是根据抽样极限误差的计算公式计算的。

（1）在重复抽样条件下，用于平均数推断和用于成数推断的必要样本容量，可分别由相应的极限误差计算公式推导而来。

■重要知识

在重复抽样条件下的必要样本容量：

用平均数推断必要样本容量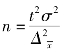

用成数推断必要样本容量

（2）在不重复抽样条件下，用于平均数推断和用于成数推断的必要样本容量，可分别由相应的极限误差计算公式推导而来。

■重要知识

在重复抽样条件下的必要样本容量：

为了保证抽样设计原定的各项要求，当样本容量n 的计算结果有小数时，应取包含原结果的整数，即应按“收入法”而不是“四舍五入”法处理。

必要样本容量计算公式汇总见表5-7。

表5-7　必要样本容量计算公式汇总表

【例5-19】　某地为了解当地100 000 户居民的收入水平，若以往抽样调查，平均月收入标准差为100 元，人均月收入少于600 元的家庭比重为15%。要求以95.45%的可靠性估计人均月收入误差超过20 元、成数误差不超过5%，至少应抽多少个家庭进行调查？

解：F（t）＝95.45%，t＝2

重复抽样条件下：

即在重复抽样条件下为达到平均数推断的要求至少要抽查100 户；为达到成数推断的要求至少要抽查204 户。

不重复抽样条件下：

即在不重复抽样条件下为达到平均数推断的要求至少要抽查100 户；为达到成数推断的要求至少要抽查204 户。

两推断指标必要样本容量不一样，应选取样本容量大的，即上例中必要样本容量为204 户。

4.影响样本容量的因素

（1）总体被研究标志的变动程度。如果总体被研究标志的变动程度大，则应抽取较多的样本单位，如果总体被研究标志的变动程度小，则可抽取较少的样本单位。(www.daowen.com)

（2）允许的误差范围。也可以说是要求的估计精度，如果允许的误差范围小，即要求的精确度高，应抽取较多的样本单位。反之，应抽取较少的样本单位。

（3）抽样推断的可靠程度。要求的可靠程度越高，则应抽取的样本单位数越多；要求的可靠程度越低，则应抽取的样本单位数越少。

5.简单随机抽样的样本容量的决定

数理统计证明，可用概率F（t）保证抽样误差不超过Δ（Δ＝t μ）。因此，在抽样调查中，可以用决定样本容量的方法来保证抽样误差不超过预定的范围。下面我们来研究简单随机抽样决定样本容量的方法：

（1）在简单随机抽样重复抽样条件下。

①测定平均数时：

②测定成数时：

（2）在简单随机不重复抽样条件下。

①测定平均数时：

②测定成数时：

运用上述公式时，还要注意下述几点：

（1）当总体单位数不大时，如果应用不重复抽样调查，必须应用不重复抽样公式；当总体单位数很大时，虽应用不重复抽样调查，但一般可以应用重复抽样公式。

（2）测定平均数时，要事先知道总体均方差σ，如果过去曾经进行过这种调查，则可利用过去最大的σ 值代替；如果过去未曾进行过这种调查，则可做调查，用试查的σ 值代替。

（3）测定成数时，要事先知道总体成数p。如过去曾经进行过这种调查，则可取最接近0.5 的值；如过去未曾进行过这种调查，则直接取p＝0.5。

【例5-20】　假定总体为3 000 单位，被研究的标志方差不少于400，当抽样误差不超过3，保证概率为0.997 3 时，需抽取多少单位？

解：已知：N＝3 000，σ2＝400，Δ＝3

t＝3（因保证概率为0.997 3）

这里因总体单位不大，故需采用不重复抽样公式。

6.类型抽样的样本容量的决定

类型抽样的公式与简单随机抽样公式，只是标志变异结构不同。在简单随机抽样时，其标志变异指标是总体的平均方差平方，而在类型抽样时，其标志变异指标是各类的平均方差平方的平均数。

（1）类型比例重复抽样。

（2）类型比例不重复抽样。

运用上述公式时应注意的问题，与运用简单随机抽样样本容量的公式相同。

类型抽样的样本容量与简单随机抽样的相同。