1.类型抽样的含义

（1）类型抽样的概念。类型抽样也叫分层抽样、分类抽样。它是运用统计分组法，把全及总体按主要标志划分为几个类型组，然后从各组中再按随机原则抽取样本单位的一种组织形式。

如图5-1 所示，分层抽样的特点为：由于通过划类分层，增大了各类型中单位间的共同性，容易抽出具有代表性的调查样本。该方法适用于总体情况复杂，各单位之间差异较大，单位较多的情况。例如，在一所高校抽取大一学生进行调查时，我们可以先把总体按系分为5 类，然后采用随机抽样的方法，分别从各系中抽取40 名学生。这样，由这200 名学生所构成的就是一个由分层抽样所得到的样本。当然我们还可以按性别、按年级或者按专业来对总体进行分类（层）。

图5-1　分层抽样图示

（2）类型抽样的优缺点。类型抽样的优点为：能提高对总体估计值的精度；能保证样本对被定义为层的那些子总体的代表性，从而得到有效的估计；操作与管理方便；能避免得到一个“差的”样本；在不同的层中可以使用不同的抽样框和不同的抽样方法。

类型抽样的缺点为：要求抽样框中的所有单元，都必须有能用于分层的辅助信息；调查框的创建较简单随机抽样和系统抽样需更多的费用，也更为复杂。

2.类型抽样的方法

经过划类分组后，确定各类型组抽样单位数一般有两种方法：

（1）不等比例抽样。即各类型组所抽选的单位数，不是按相同比例确定，而是根据情况具体确定各层抽样比例。如按各类型组标志值的变动程度来确定，变动程度大的多抽一些单位，变动程度小的少抽一些单位，没有统一的比例关系。

【例5-12】　某高校为了解10 000 名大一学生对在校恋爱的态度，采取分层抽样方式，随机抽取2.00%即200 人进行调查。现把该校5 个系分为5 组（层），每个组（层）随机抽查40 人，由于各系学生人数不同，而要抽取相同人数调查，故各系抽样比例不相等，是不等比例抽样。具体抽样数见表5-3：

表5-3　某校各系抽取人数表

（2）等比例抽样。即按照样本单位数在各类之间分配的比重与总体在各类之间分配相同的比重进行抽样。各层抽样数ni＝Ni·（n／N），式中，n／N 为总体抽样比例，为定值（如2.00%），Ni为某层总体单位数。如上例中采取等比例抽样方式抽取样本单位数，具体见表5-4：

表5-4　某校各系抽取人数表

在实际工作中，由于事先很难了解各组的标志变异程度，因此，大多数类型抽样采用等比例类型抽样法。

3.类型抽样的抽样推断

根据各种方差之间的关系，总方差（σ2）等于组间方差与平均组内方差之和。由于类型抽样对于各组来说是全面调查，而对于每一组内部来说是抽样调查，所以，类型抽样的误差仅与组内方差有关，而与组间方差无关。因此，当测定平均数指标时，计算抽样误差不是用总方差，而是用各组组内方差的加权算术平均数。根据同样的道理，在测定成数指标时，计算抽样误差不是用抽样成数的方差p（1-p），而是用各组方差的加权算术平均数［注意不是p（1-p）］。所以，类型比例抽样和必要抽样数目的公式如下。

（1）抽样平均误差确定。

①在重复抽样条件下。

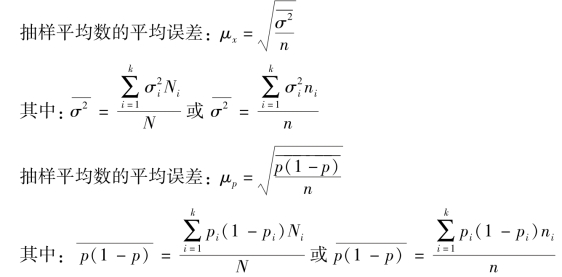
②在不重复抽样条件下。

抽样平均数的平均误差：

抽样平均数的平均误差：

在实际工作中，同样不知道全及总体各类的组内方差，所以，同样用各类型组内方差来代替。

（2）类型抽样推断的步骤。根据类型抽样的特点，可归纳出类型抽样推断的步骤（以平均数的推断为例）：

①计算各组的平均数：

②计算各组的组内方差：

③计算抽样的样本平均数：

(www.daowen.com)

④计算抽样的组内方差的平均数：

⑤计算抽样的平均误差：

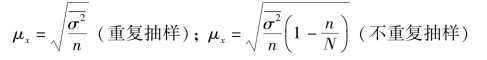
⑥计算抽样推断极限误差：

Δx＝tμx或确定抽样推断的置信度F（t）。

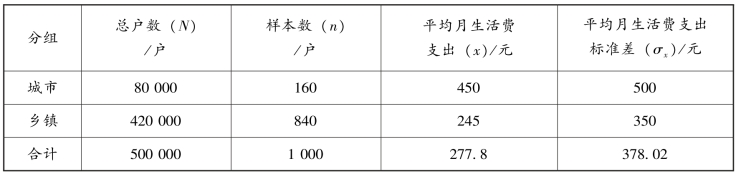
【例5-13】　某地家计调查中，从500 000 户中按0.2%抽取1 000 户进行调查，了解生活费支出情况，现采用分层抽样方式，按居住地分为城市和乡镇两类，从各类中随机抽取样本单位，所调查资料经整理计算见表5-5：

表5-5　调查资料经整理计算表

现要求以95.45%的概率保证程度推断该地人均月生活费用支出水平。

样本平均数：

组内方差的平均数：

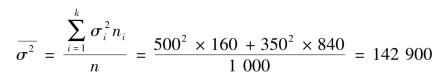
抽样的平均误差：

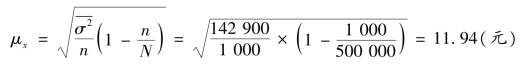
抽样推断极限误差：

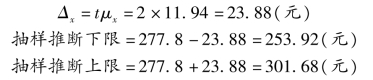
则该地人均月生活费用支出水平在253.92 元和301.68 元之间的概率保证程度为95.45%。

【例5-14】　某地家计调查中，从500 000 户中按0.2%抽取1 000 户进行调查，了解生活费支出情况，现采用分层抽样方式，按居住地分为城市和乡镇两类，从各类中随机抽取样本单位，了解人均月生活费支出500 元以上的户数比重。所调查资料经整理计算见表5-6：

表5-6　调查资料经整理计算表

现要求以95.45%的概率保证程度推断该地人均月生活费用支出500 元以上的户数比重。

人均月生活费用支出500 元以上的户数比重：

抽样推断平均方差：

抽样推断平均误差：

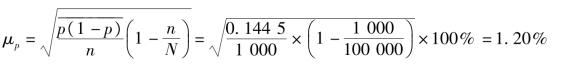
抽样推断极限误差：Δp＝tμP＝2 ×1.20%＝2.40%

抽样推断下限＝19%-2.40%＝17.60%

抽样推断上限＝19% ＋2.40%＝21.40%

95.45%的概率保证程度推断该地人均月生活费用支出500 元以上的户数比重在17.60%和21.40%之间。