1.抽样极限误差的概念

抽样极限误差是指样本指标和总体指标之间抽样误差的可能范围，也称为抽样误差范围。由于总体指标是一个确定的数，而样本指标是围绕着总体指标上下变动的量，它与总体指标可能产生正离差，也可能产生负离差，样本指标变动的上限或下限与总体指标之差的绝对值就可以表示抽样误差的可能范围Δ。抽样极限误差的大小可以根据有关方法进行估计；但在实践中，人们也常常根据调查目的和任务规定该项调查极限误差的大小，此时，极限误差也称为允许误差，利用它对调查结果的误差范围进行约束，以保证调查结果的精确度满足调查任务的要求。

上面等式可以变换为下列不等式关系：

2.抽样极限误差的计算

基于概率估计的要求，抽样极限误差通常需要以抽样平均误差或μp为标准单位来衡量，从而将极限误差表示为t 倍的平均误差，而t 是测量估计可靠程度的一个参数，称为抽样平均误差的概率度。抽样估计的概率度是表明样本指标和总体指标的误差不超过一定范围的概率保证程度。由于样本指标值随着样本的变动而变动，它本身是一个随机变量，因而样本指标和总体指标的误差仍然是一个随机变量，并不能保证误差不超过一定范围这个事件是必然事件，而只能给以一定程度的概率保证。因此，就有必要来计算样本指标和总体指标的误差不超过一定范围的概率大小，即计算样本指标落在一定区间范围内的概率，这种概率称为抽样估计的概率度。

■重要知识

极限误差、抽样平均误差、抽样平均误差的概率度的关系式为：

(www.daowen.com)

从抽样极限误差的计算公式看，极限误差与概率度t 和抽样平均误差三者之间存在如下关系：

（1）在保持抽样平均误差不变的情况下，增大t 值，把握程度相应增加，误差范围也随之扩大，这时估计的精确度将降低；反之，要提高估计的精确度，就得减小t 值，此时把握程度也会相应降低。

（2）在t 保持不变的情况下，抽样平均误差小，则误差范围就小，估计的精确度就高；反之，抽样平均误差大，误差范围就大，估计的精确度就低。

根据数理统计的有关理论，抽样极限误差与抽样平均误差（Δ／μ）的比值与概率保证程度是一一对应的关系，每一个t 值都对应一个概率保证程度。在大样本条件下，可以根据“正态分布概率表”查到它们之间对应的值。

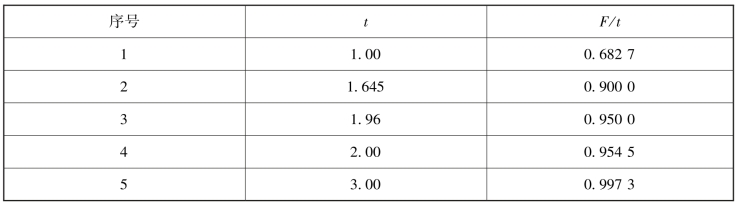
表5-1 所示是一些常用的t 值和对应的概率数值。

表5-1　常用的t 值和对应的概率数值

【例5-4】　用【例5-1】 资料，若以95.45%的概论度估计，则抽样极限误差是多少？

抽样极限误差＝2 ×9.995＝19.99（小时）

抽样推断时不能只考虑提高估计的把握程度或只考虑缩小允许误差。若误差范围太大，则估计精确度太低，这时尽管估计的把握程度非常接近l00%，抽样估计本身也会失去意义；反之，若把握程度太低（错误估计的可能性太大），尽管误差范围很小，估计结果也无多大作用。因此，进行抽样估计时必须在两者之间进行慎重选择。实际处理时有两种考虑方法，一是先提出推断可靠性要求，然后根据其所对应的t 值及抽样平均误差计算误差的可能范围；二是先提出允许的误差范围（即极限误差），再求出t 值，查找其对应的概率保证程度。两种方法视具体问题而确定。