标志变异指标是由多个指标组成的统计指标体系，主要包括全距（极差）、平均差、标准差和变异（离散）系数四个基本指标。

1.全距

全距又称极差，是总体各单位标志值的最大值和最小值之差，通常用“R”表示。由于全距是一个数列中两个极端值之差，故又称极差。全距越大，说明标志值变动的范围越大，集中趋势越弱，代表集中趋势的平均指标的代表性越低。全距越小，则集中趋势越强，平均指标的代表性越高。

对于未分组资料，计算公式为：

对于分组资料，计算公式为：

式中，Xmax表示总体中最大变量（标志）值；Xmin表示总体中最小变量（标志）值。

如前例甲、乙两班组日产量的全局分别为：

两组工人的平均日产量均为70 件，但甲组全距大，说明日产件数波动范围大，平均日产量的代表性小。而乙组全距小，说明工人日产件数波动范围较小，所以平均日产量的代表性就大。

应该指出，根据未分组资料计算的全距，结果仅仅是一个近似值。原因是在统计分组过程中，最大变量值组上限一般要大于总体最大变量值，而最小变量值组下限一般要小于总体最小变量值，况且，为了统计分析的便利，也一般用5 或10 的倍数作为组限。因此，最大变量值组上限往往与总体最大变量值不相等，最小变量值组下限也往往与总体最小变量值不一致。

全距最大的特点是计算简便，容易被人们接受和理解。它是测定离散程度的最简便方法。实际工作中，常用于工业产品质量检查和控制。但是，全距只是根据变量值计算而来的，容易受极端数值的影响。因此，不能全面反映所有变量值的综合变动程度，有很大的局限性。为全面表明总体的变异程度，还应当进一步计算其他变异指标。

2.平均差

平均差是各单位标志值对平均数离差绝对值的平均数。离差是总体各单位标志值与算术平均数之差，用公式表示为由于各标志值与算术平均数的离差总和恒等于零，即因此在计算平均差时，采用离差绝对值的方法计算。

根据所掌握的资料不同，平均差的计算可分为简单算术平均式和加权算术平均式两种。

（1）简单算术平均式。如果所掌握的资料是未分组的资料，可用简单算术平均式计算平均差。公式为：

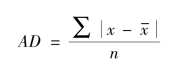
式中，AD 为平均差，其他符号同前。

【例4-26】　某车间5 名工人日产零件数资料为12 件、13 件、14 件、14 件、15 件，平均每人日产量x-＝13.6 件，见表4-18。试计算日产零件数平均差。

表4-18　5 名工人日产零件离差计算表

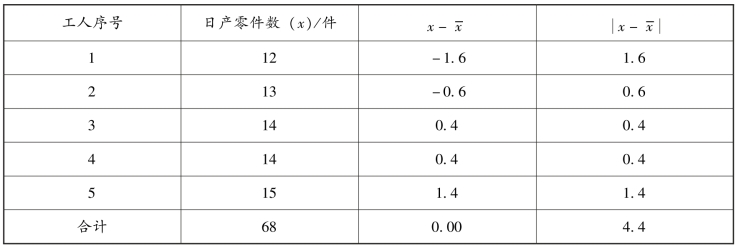
解：工人日产零件数的平均差为：

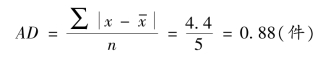
（2）加权算术平均式。如果所掌握的是分组资料，则应采用加权算术平均式计算平均差。其公式为：

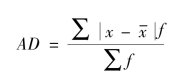
【例4-27】　某企业工人日产量见表4-19，求日产量的平均差。

表4-19　某企业工人日产量的平均差计算表

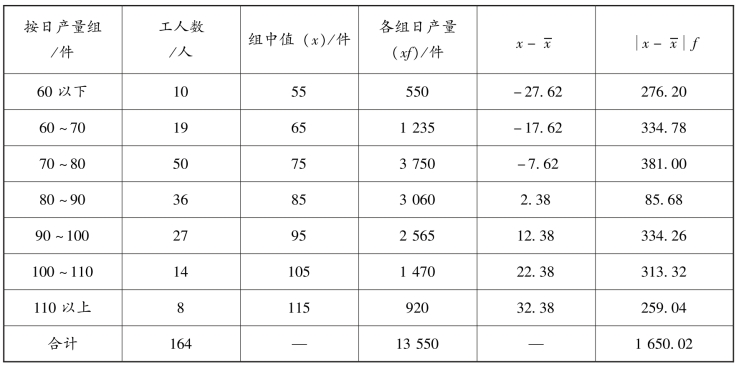
平均差的意义明确，同全距相比，计算的依据是总体所有变量值，具有普遍性，能够准确反映总体变异的状况。但是，由于平均差是用总体各单位变量值同总体算术平均数的离差的绝对值来计算的，很难进行更深入的数学计算，因而在实际应用上受到很大限制。

3.标准差

依据所掌握的资料不同，标准差的计算分为简单平均式和加权平均式两种。

（1）简单平均式。对于未分组资料，采用下列公式计算标准差：

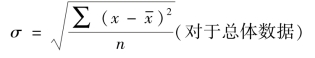
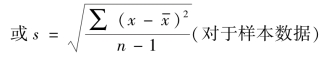
【例4-28】　仍用【例4-26】 资料，求日产零件数的平均差（参考表4-20）。

表4-20　某企业工人日产量的简单标准差计算表

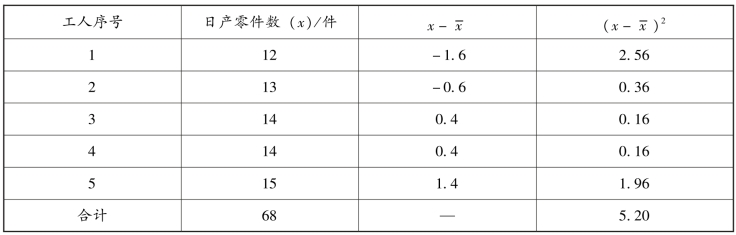
工人日产零件数的标准差为：(www.daowen.com)

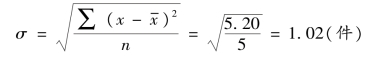
（2）加权平均式。如果掌握的是分组资料，采用下列公式计算标准差：

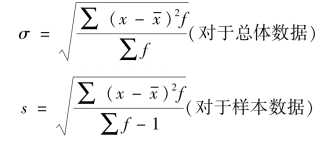
【例4-29】　某企业工人日产量情况见表4-21，求标准差。

表4-21　某企业工人日产量的加权标准差计算表

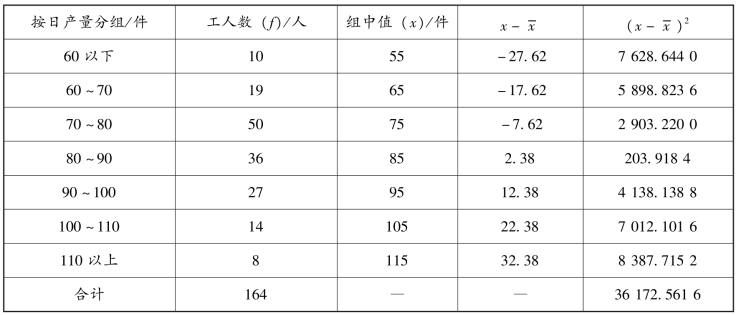
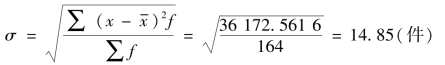
4.变异系数

标志变异指标数值的大小，不仅受变异程度的影响，而且受平均水平高低的影响，因此，比较不同总体的变异程度的高低，不能简单地根据平均差或标准差的大小来比较，而应该将平均差、标准差与相应的平均数对比，计算标志变异的相对指标后进行比较，即计算标志变异系数。

变异系数是反映一组数据相对差异程度的变异指标，是各变异指标与其算术平均数的比值。变异系数是一个无名数，可以用于比较不同数据的离散程度，也称离散系数。变异系数主要有全距系数、平均差系数和标准差系数，其中最常用的是标准差系数。

全距与总体平均数对比所得到的比值称为全距系数，计算公式为：

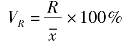
平均差与总体平均数对比所得到的比值称为平均差系数，计算公式为：

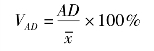
标准差与总体平均数对比所得到的比值称为标准差系数，计算公式为：

【例4-30】　已知甲、乙两班组工人日产量资料如下（单位：件）。

甲组：60、65、70、75、80

乙组：2、5、7、9、12

要求：计算两班组工人的平均日产量，并分析判断哪个班组的平均日产量代表性大。

解：（1）求各组平均日产量和标准差。

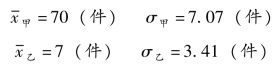
因为，σ甲＝7.07 ＞σ乙＝3.41，说明乙组工人日产量的平均差异较小，平均日产量代表性较大。但是通过计算标准差系数得出相反的结论。

（2）求标准差系数。

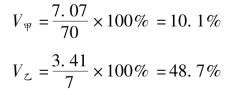
必须指出，当比较两组数据的离散程度时，如两组平均数相等，可以直接比较标准差；如两组平均数不等，则需比较两组的离散系数。因为标准差的大小，不仅取决于总体的变异程度，而且受变量值水平的影响。总体各单位变量值水平越高，标准差就越大，反之就越小。在这种情况下，只有通过标准差系数的比较，才能得出正确的结论。

计算结果表明，乙组的变异程度大于甲组，因而甲组平均产量的代表性更大。

相关知识图示

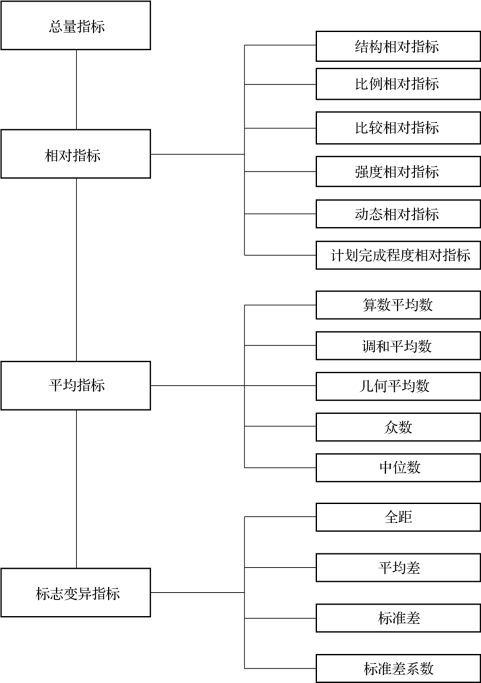
本章小结

本章主要介绍了通过综合指标法来对社会经济现象进行分析和研究的方法，主要通过完成总量指标、相对指标、平均指标和标志变异指标分析技术等相关任务来对总体现象的数量方面进行计算和分析。

总量指标是统计指标中最基本的指标，它的计算是否科学合理会直接影响相对指标和平均指标的准确性。总量指标主要反映社会经济现象的总体规模和水平，而相对指标主要反映现象总体内部的结构、比例、发展状况和彼此间的关系，以及对计划完成情况的检查。相对指标有多种，每种指标只能从某一角度出发，反映事物的一个侧面，很难用某一相对指标来说明问题的全部，因此我们必须注意把多种指标结合运用。相对指标的一个重要特点，就是将对比的总量指标进行了抽象。因此，在应用相对指标说明和分析问题时，应该使之与相应的总量指标联系起来观察才能克服认识上的片面性，使我们获得对所研究现象的全面认识。

平均指标是社会统计中非常重要且应用十分广泛的一种综合指标。应掌握算数平均数、调和平均数、几何平均数、众数和中位数的特点、计算方法和应用条件，其中算数平均数是应用最广泛的。平均指标描述的是总体的集中趋势，而标志变异指标是描述总体的离中趋势，它们是两个意义相反的指标，我们要从集中趋势和离中趋势两个方面去认识总体的分布特征，解决有关经济和技术问题。

思考题

1.什么是数据的集中趋势？度量数据集中趋势的指标有哪些？

2.什么是数据的离散程度？度量数据离散程度的指标有哪些？

3.在不同的分布类型中（对称、左偏和右偏分布），平均数、众数和中位数之间的关系分别是怎样的？

即测即评

延伸资料