1.几何平均数的概念和特点

几何平均数不同于算术平均数和调和平均数，它是n 项变量值连乘积的n 次方根，是计算平均比率和平均速度时比较适用的一种方法，符合人们的认识规律。例如，有甲、乙两种商品，甲商品的价格从200 元上涨到250 元，其价比为1.25（250/200），其上涨率为25%，而乙商品的价格从250 元下降到200 元，其价比为0.8（200/250），即降低率为20%。如果单纯从价格变动角度看两者拉平，应当是没有变动的，但是这两种价比按算术平均法计算平均价比为1.025［（1.25 ＋0.8）÷2］，即上涨了2.5%。如果按调和平均法计算，平均价比为：

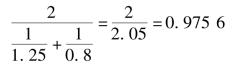
即平均下降了2.44%。很明显，由于甲商品涨幅超过了乙商品的涨幅，所以按算术平均法计算的结果偏高，按调和平均法计算的结果偏低，都不符合实际。实际是甲商品上涨了50元，乙商品下降了50 元，从绝对数来说为0，即甲、乙两种商品平均来说没涨没跌。计算表明，用几何平均法最合适，即平均价比＝＝1 或100%，表明两种商品价格平均来说没涨没跌。所以，凡是变量值的次数等于总比率或总速度的现象都可用几何平均法计算平均数。

2.几何平均数的计算方法

由于掌握的资料不同，几何平均数也分简单几何平均数和加权几何平均数两种。

（1）简单几何平均数。

式中，G 为几何平均数；x 为各变量值；n 为变量值的个数；∏为连乘积符号。

【例4-15】　某地区2006—2010 年工业品的产量分别是上年的107.6%、102.5%、100.6%、102.7%、102.2%，计算该地区5 年的平均发展速度。

为进一步了解它的实质，采用对数计算：

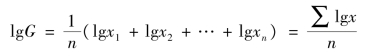
由此可见，几何平均数的对数，实质上是各个变量值的对数的算术平均数。求出几何平均数的对数后，再由反对数表查出真数，即几何平均数。

【例4-16】　某机械厂生产某种机器，下设毛坯、粗加工、精加工和装配四个连续作业的车间。某批产品其毛坯车间制品合格率为97%，粗加工车间制品合格率为93%，精加工车间制品合格率为87%，装配车间制品合格率为91%，求各车间制品平均合格率。

解：方法一：

方法二：按对数方法计算车间产品平均合格率（表4-9）。

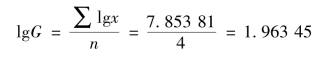
反对数的产品平均合格率：G＝91.93%。

表4-9 所示为车间产品平均合格率。(www.daowen.com)

表4-9　车间产品平均合格率

（2）加权几何平均数。当计算几何平均数的每一个变量值的次数不相等时，则需采用加权几何平均数法，其计算公式为：

式中，f 为变量值的次数；∑f 为次数总和；其他符号同前。

将上述公式两边取对数，则：

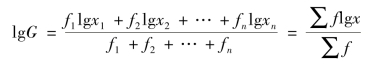
可见，加权几何平均数的对数，就是各变量值对数的加权算术平均数。求出几何平均数的对数后，再求反对数找出真数，即几何平均数。

【例4-17】　某投资银行25 年的年利率分别是1 年8%、4 年5%、8 年4%、10 年3%、2 年2%，求平均年利率。（年利率按复利计算。）

解：在计算平均年利率时，根据研究对象性质必须先将各年利率加100%换算成各年本利率，然后按加权几何平均法计算平均年本利率，再减100% 的平均年利率，列表计算如下。

方法一：采用几何平均数的基本公式计算。

方法二：按对数的方法计算。表4-10 所示为平均年本利率计算表。

表4-10　平均年本利率计算表

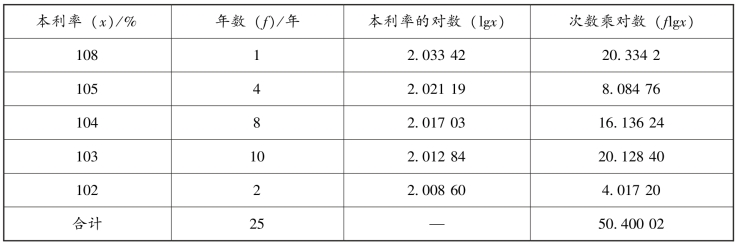
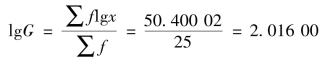
求反对数得本利率：

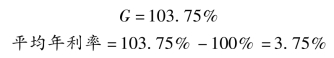
结果说明，25 年间的平均年本利率为103.75%，平均年利率为3.75%。

我们已知道，平均指标按其计算方法的不同，可分为数值平均数和位置平均数两类。前面学过的算术平均数、调和平均数和几何平均数均是数值平均数，是根据总体各单位的标志值计算的平均数；而位置平均数是根据分布数列中某些标志值所处的位置来确定的平均数，即下面将要介绍的众数、中位数等。