调和平均数是平均数的一种，它是根据变量值的倒数计算的，是变量值倒数的算术平均数的倒数，故也称倒数平均数。在社会经济统计中，往往由于缺乏总体的单位数资料，而不能直接采用算术平均的方法计算，这时，就需要把算术平均数的形式加以改变，而采用另一种计算方法。所以，实际工作中，它主要是作为算术平均数的变形来使用。其主要特点是用特定的权数（m＝xf）加权，其变量值多为相对数和平均数。在计算平均数时，由于受到所掌握资料的限制，往往不能直接用加权算术平均数的方法计算，而需要按照平均数基本公式的需要，算出所需总体单位数，或者相当于总体单位数的数字，这时所用的方法，就是加权调和平均数的方法。调和平均数有简单调和平均数和加权调和平均数两种。

1.简单调和平均数

为了方便了解调和平均数的概念和计算方法的说明，请先看下面的简单例子。

【例4-13】　市场上早、中、晚某种蔬菜价格分别是早上0.67 元/千克、中午0.5 元/千克、晚上0.4 元/千克。现在，我们分别按四种购买方式购买这种蔬菜，分别计算该种蔬菜的平均价格是多少。

购买方式一：早、中、晚各买1 千克。

则蔬菜的平均价格为：

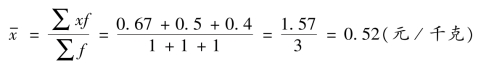
购买方式二：早、中、晚分别买1 千克、2 千克、3 千克。

则蔬菜的平均价格为：

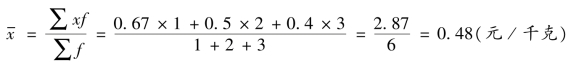
购买方式三：早、中、晚各买1 元钱的。

这种情况下，计算蔬菜平均价格比上述两种方法稍微复杂一些。计算出早、中、晚花费1 元钱所购买蔬菜的数量，即千克数，然后再计算蔬菜的平均价格。

蔬菜的平均价格为：

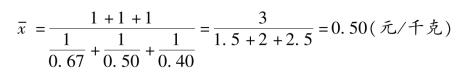
这种计算平均指标的方法同算术平均法有很大的不同。因为，资料中缺乏总体单位总量（总购买量），所以就不能直接用计算算术平均数的方法求平均价格。为了达到计算目的，首先要用标志值的倒数计算出单位总量来，然后计算平均指标（本例为平均价格）。调和平均数因此而得名，也正是这一原因，调和平均数又称倒数平均数，一般用“H”表示。

将第三种购买方式推广到一般，可得到简单调和平均数的计算公式为：

式中，H 为调和平均数；其他符号同前。

购买方式四：早、中、晚分别买1 元、2 元、3 元的。(www.daowen.com)

与第三种方式一样，我们还需先计算出早、中、晚购买蔬菜的数量，即千克数，然后再计算蔬菜的平均价格。

蔬菜的平均价格为：

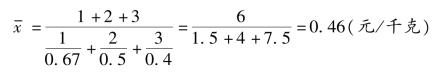
在上述计算平均价格的过程中，早、中、晚三个时段购买蔬菜所花费的现金（各组标志总量）是计算平均价格的权数，这种统计方法称为加权调和平均法，计算出的平均数称为加权调和平均数。

2.加权调和平均数

将第四种购买方式推广到一般，可得到加权调和平均数的计算公式为

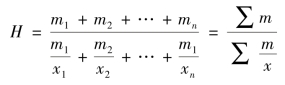
式中，m 为标志总量（m＝xf）；其他符号同前。

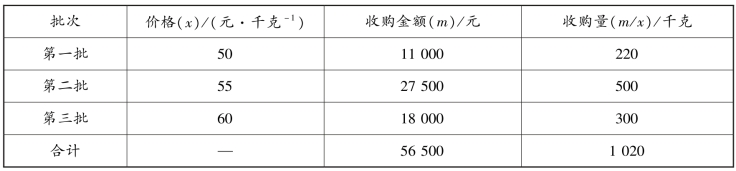
【例4-14】　某农产品收购部门，2010 年购进三批同种产品，每批产品的价格及收购金额见表4-8。求三批产品的平均价格。

表4-8　某农产品收购部门收购情况

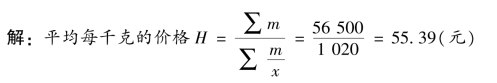
由此不难看出，加权调和平均数是一般，而简单调和平均数是特殊，也就是说简单调和平均数只是加权调和平均数的一种特殊形式，即当各组权数（m）相等时，加权调和平均数就变形为简单调和平均数。即当m1＝m2＝…＝mn＝A 时，

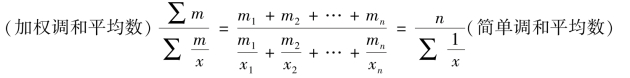
需要说明的是，调和平均数是各标志（或变量）值倒数的算术平均数的倒数，是在资料受到限制的条件下算术平均数的一种变形，它与算术平均数并无本质区别，即

若设m＝xf则有f＝m／x代入加权算术平均数公式，得：

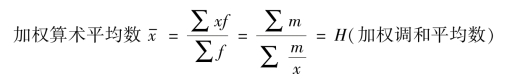
如【例4-14】 中，m 为收购金额，即权数；x 为变量（标志）值；分子是总体标志总量；分母是收购量之和，即总体单位总数。所以，调和平均数仍然是以总体标志总量除以总体单位总数计算的。它在经济内容和计算结果上与算术平均数一致，只是由于计算时依据的资料不同，而在计算公式和计算过程方面有别于算术平均数。

那么，如何判断在什么情况下可以采用算术平均数或调和平均数呢？关键在于应以算术平均数的基本公式为依据进行判断，即必须满足公式的分子为总体标志总量，而分母必须是总体单位总数。当已知分母资料，即已知总体单位总数时，应采用算术平均数公式计算；当已知分子资料，即已知总体标志总量时，应采用调和平均数公式计算。