1.统计图的定义和结构

统计图是统计资料的一种表达方式，它可以简洁、直观地表示统计表中枯燥的数据，可以帮助我们从众多的数据中发现规律，可以更迅速、更有效地传递信息，给人明确和深刻的印象。

统计图可以表明现象的规模、水平、结构、对比关系、依存关系、发展趋势和分布状况。如果说统计表能够集中有序地表现统计资料，统计图则能够将统计资料展示得更为生动、具体，便于人们直观地认识事物的特征。

统计图可以手工绘制，也可以用电子计算机绘制生成。随着计算机技术的不断发展，计算机制图功能日益强大，使得统计图的制作更加方便和精确。目前，常用Excel 绘制统计图。

统计图一般包括以下几个基本要素：

（1）标题。标题有图表标题、数值轴（横轴、纵轴）标题。图表标题是统计图的名称，它简明扼要地说明全图的基本内容，一般置于统计图的下端。例如，图3-4 中图表标题是“2018 年中国人口年龄金字塔”，简要地说明了该图反映的研究对象（中国人口）、研究内容（年龄性别人口结构分布），以及研究内容发生的时间（2018 年）等要素。图3-4 中纵轴标题是年龄，即2018 年时的年龄，从“0 ～4 岁组”至“80 岁＋组”依次在纵轴上排列；横轴标题是人口数（单位百万），2018 年0 ～4 岁的男性人口接近4 200 万人，而0 ～4 岁的女性人口接近4 000 万人，性别比例约为105∶100，性别比出现失调。

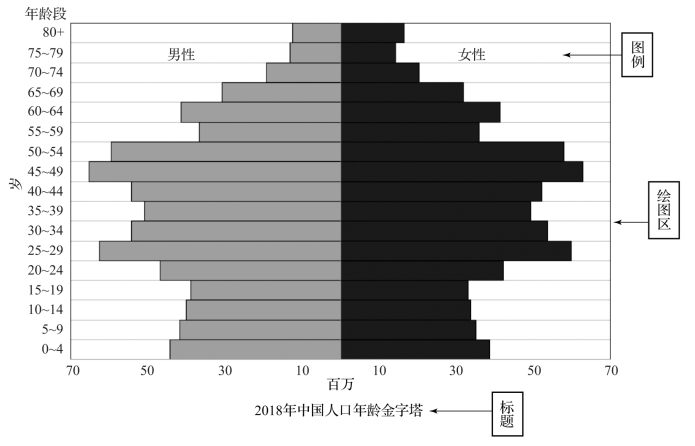
图3-4　统计图的结构

（2）绘图区。将统计表中的数据或原始数据绘制出图形的区域。例如，在图3-4 中，根据调查可知2018 年10 ～14 岁的女性人口数为3 500 万人，在纵轴上找到10 ～14 岁的所在位置，并将代表人口数的条形向横轴方向延伸至3 500 万人口的位置，如此便绘出了2018年10 ～14 岁女性人口的人口数，依次类推，可以根据各组的男女人口数，分别在图中绘出相应的条形，最终将得到如图3-2 所示的人口年龄金字塔图形，直观、形象地反映出我国各年龄段的人口性别比和人口的年龄结构以及变化趋势。

（3）图例。图例用来表明图中的数据系列，一般置于图表的右上方。如果只有一个数据系列则不需要图例。例如，图3-4 中包括男女两个数据系列，在图例中标出浅颜色代表男性，深颜色代表女性，以示区别。

2.统计图的种类

统计图的种类很多，常用的有饼图、柱状图、直方图、折线图等。

（1）饼图。根据表3-6 的数据做出的不同品牌饮料市场占有率的统计图，即“图3-5不同品牌饮料的市场占有率”，从图中可以了解到每一种饮料的市场占有率，其中可口可乐的占有率最高，占30%。饼图中的每一块“小饼”代表一个分组标志，其面积大小代表该分组标志在总体中所占的比例，比例越大，则“小饼”的面积越大，所有“小饼”加在一起就构成一个完整的圆饼，即表示各组的频率之和为1。饼图由于其简单、直观的特点在市场占有率的分析中运用较广。饼图适用于任何分组数据，但更多地应用于定类和定序尺度的数据。

图3-5　不同品牌饮料的市场占有率

（2）柱状图。根据表3-8 的数据绘制社区家庭拥有孩子数柱状图。横轴表示各组的代表值，纵轴表示频数或频率，依据各组组距的宽度和频数（频率）的高度绘成柱状形。从图3-6 的图例中可以看出，纵轴为户数，表示社区家庭拥有孩子数的频数，其中拥有1 个孩子的家庭户为200 户，频数最高。从图中可见，柱状图的各个条形柱并不相连，原因在于所反映的数据是离散型定距数据或定序、定类尺度数据，这些数据的特征是其在坐标轴上不连续，社区家庭拥有孩子数0、1、2、3 个就是离散型数据。由此我们知道，柱状图只能使用于离散型定距数据或定序、定类尺度数据，不能用于连续型的定距数据。

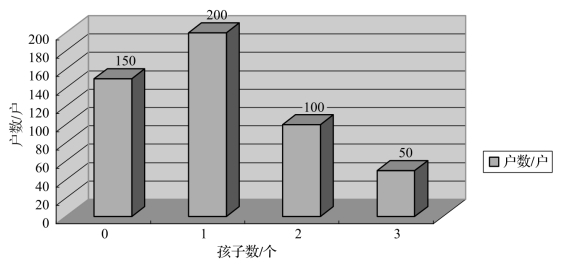
图3-6　社区家庭拥有孩子数柱状图

3.直方图

直方图是用矩形的宽度和高度来表示频数分布的图形。绘制直方图时，横轴表示各组组限，纵轴表示频数或频率，依据各组组距的宽度和频数（频率）的高度绘成矩形。图3-7是根据表3-12 绘制的直方图。图3-4 的人口年龄金字塔也是典型的直方图应用，只是将频率（频数）变换到横轴。横轴和纵轴的具体设置可以根据研究和表述的需要进行变化，一般情况下，我们在绘制直方图时习惯用横轴表示分组坐标，用纵轴表示频率（频数）。直方图与柱状图存在细小的差异，直方图的长条形紧密地排列在一起，而柱状图的长条形是分散地排列，原因就在于我们前面提到的离散数据与连续数据之间的差别。因此，我们还必须在应用中注意直方图只适用于连续型的定距数据。

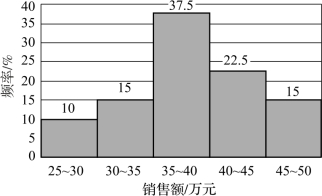
图3-7　某百货公司商品销售额分布图

4.折线图

折线图是以线段的起伏表示数量分布的特征。绘制时，横轴表示变量值，纵轴表示频数或频率，先根据变量值和其频数在坐标轴上绘出相应的点，再用折线将所有的点连接起来，直观地表现数量分布的变动规律。可以用单变量频数分布数列来绘制，也可以用分组数据来编制，分组数据各组用其组中值作为代表值。图3-8 是根据表3-12 绘制的折线图，该图直观地反映出商品销售额分布的特征，销售额在35 万～40 万元的天数最多，高于40 万元和低于35 万元的销售额的天数逐渐下降。

当所观察的组距越小且组数越多时，所给出的折线图就会越光滑，逐渐形成一条光滑的曲线，这种曲线即频数分布曲线，反映了数据或统计量的分布规律。统计曲线在统计学中很重要，是描述各种统计量和分布规律的有效方法。在日常生活和经济管理中，较常见的有四种曲线，即正态分布曲线、偏态曲线、J 形曲线和U 形曲线。

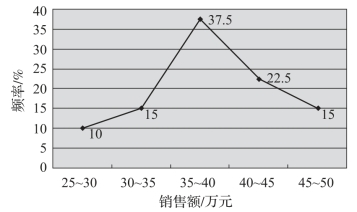
图3-8　某百货公司商品销售额折线图(www.daowen.com)

正态分布曲线也称钟形曲线，如图3-9 中的（a）图所示，“中间大，两头小”，即中间的变量值分布频数多，靠近两边的变量值分布的频数少，形状为左右对称，犹如挂着的钟。这是客观事物数量特征表现最多的一种频数曲线，例如，人的身高、体重、智商、考试成绩、农作物产量等。

偏态曲线根据尾部拖向哪一方又可分为右偏和左偏两种曲线，如图3-9 中的（b）图所示为右偏分布，（c）图所示为左偏分布。例如，人均收入分配的曲线就是右偏曲线，即低收入的人数较多，在收入较低的左边形成高峰，高收入的人数较少，且收入越高的人越少，在右边形成了一个细长的尾巴。

J 形曲线包括正J 形和倒J 形分布，比较常见的例子是西方经济学中的供给曲线和需求曲线。供给曲线如图3-9 中的（d）图所示，随着价格的增加，供给量在不断增加；需求曲线如图3-9 中的（e）图所示，随着价格的增加，需求量在不断减少。

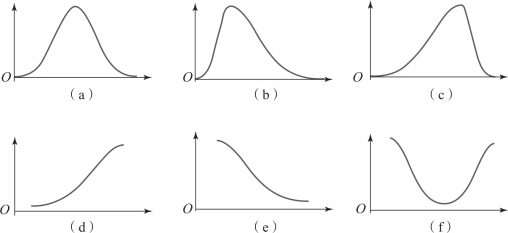
图3-9　几种常见的频数分布

（a）正态分布曲线；（b）右偏分布；（c）左偏分布；（d）正J 形分布；（e）反J 形分布；（f）U 形分布

U 形曲线又称生命曲线或浴盆曲线，人和动物的死亡率近似服从U 形曲线分布。婴儿由于抵抗力弱，死亡率很高。随着对新环境的适应和年龄的增长，死亡率逐渐降低。到了中年时期，死亡率最低；进入老年后，身体出现衰退性病变，死亡率又逐渐提高。另外，人们的闲暇时间也是呈U 形曲线分布的。婴儿和少儿时期，人们的闲暇时间最多；随着年龄的增长，开始上学、就业，闲暇时间逐渐减少；人到中年事业达到最高峰，同时家庭的负担也最重，上有老下有小，工作和家庭的双重压力使得中年人的闲暇时间最少；随着中年步入老年，逐渐退出工作岗位，孩子也都长大离开家庭，老年人的闲暇时间又逐渐增加。

本章小结

（1）统计整理就是根据统计研究的目的和任务的要求，对收集得到的初始数据进行审核、分组、汇总，使之条理化、系统化，变成能反映总体特征的综合数据的工作过程。统计整理的全过程包括对统计资料的审核、分组、汇总和编制统计图表四个环节。

（2）统计分组就是根据研究任务的要求和现象总体内在的特点，将统计总体按照一定的标志分为若干个组成部分的一种统计方法。统计分组的关键是分组标志的选择和各组界限的合理划分。

（3）标志分组根据分组标志的性质不同划分为按品质标志分组和按数量标志分组；按分组标志的多少划分为简单分组和复合分组。

（4）在统计分组基础上，将总体的所有单位按组归类整理，并按一定顺序排列，形成总体中各个单位在各组间的分布，称为次数分配或分配数列。

（5）变量分配数列简称变量数列，是按照数量标志进行分组所编制的分配数列。

（6）单项式数列一般只能用在变量值变化幅度不大的离散型变量中。连续型变量和变量值较多的离散型变量适合编制组距式变量数列。划分连续型变量的组限时，采用“重叠分组”和“上组限不在组内”原则。

（7）等距分组就是标志值在各组保持相等的组距，凡是在标志值变动比较均匀的情况下，都可采用等距分组。异距分组就是分组的组距不等。在标志值分布很不均匀，变动幅度很大时应考虑采用异距分组。

（8）统计调查所得来的原始资料，经过汇总整理，得到说明社会现象及其发展过程的数据，将这些数据按一定的逻辑顺序排列在表格上，就形成了统计表。

（9）统计表根据主词是否分组和分组的程度，分为简单表、分组表和复合表三种。统计表按宾词进行分类，可分为宾词简单分组和宾词复合分组两种。

（10）统计图是统计资料的一种表达方式，它可以简洁、直观地表示统计表中枯燥的数据，可以帮助我们从众多的数据中发现规律，可以更迅速、更有效地传递信息，给人明确和深刻的印象。常用的统计图有饼图、柱状图、直方图、折线图等。

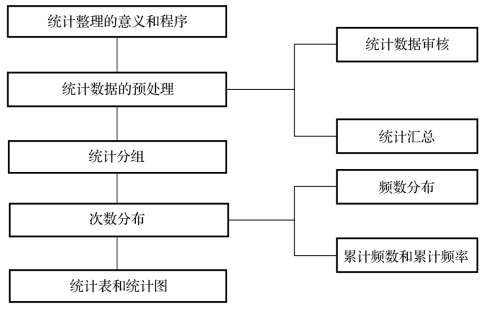
相关知识图示

思考题

1.试述统计整理在统计研究中的重要性。

2.如何正确确定按数量标志分组的分组界限？

3.组距和组数的关系如何？如何正确地确定组距和组数？

即测即评