统计分组根据分组标志的性质，可分为按品质标志分组和按数量标志分组；根据分组标志的多少，可分为简单分组和复合分组。统计分组方法一般是指这两种分组方法。

1.按品质标志分组

按品质标志分组，也称品质分组。即以反映现象属性特征的标志作为分组标志，将总体分为若干不同的组成部分。一般来说，对于以定类尺度或定序尺度计量的，采取品质分组。品质分组按复杂程度大致可分为比较简单的和比较复杂的两种情况：比较简单的分组，分组标志一经确定，一个品质标志表现即一组，组的名称和组数也随之确定。例如，人口按性别分为男性和女性，分出的各组在界限上、性质上是稳定的、明确的。但是，国民经济按部门分组、人口按职业分类、产品按用途分类，各组的界限很难划分。又如，一家市场调查公司为研究不同品牌饮料的市场占有率，对随机抽取的一家超市进行了调查。调查员在某天对50 名顾客购买饮料的品牌进行了记录，如果一个顾客购买某一品牌的饮料，就将这一饮料的品牌名字记录一次。对收集的数据进行统计分组，每种饮料品牌为一组（表3-6）。

表3-6　不同品牌饮料的分组表

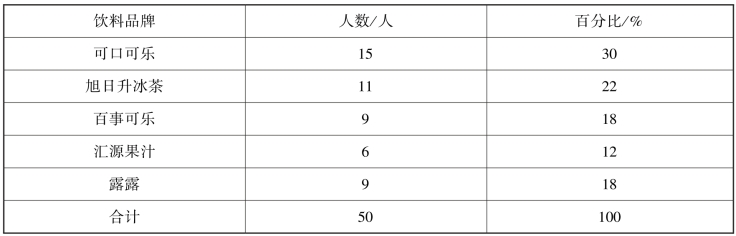
表3-7 是比较复杂的品质分组，该表记录的内容来自2013—2015 年厦门大学对流动人口结婚登记地点的调查结果，该表用了三个分组变量，一是按“有无外出经历”这个标志，将调查总体分成农村未外出人口、农村有流动经历人口、农村流入厦门市打工人口；二是在有外出经历的人口中，还以利用“是否在外出前初婚”的标志将总体分成外出前初婚和外出后初婚；三是按标志“实际结婚登记地”，将总体分成在男方户口所在地登记结婚和在女方户口所在地结婚。通过这个复合式品质分组表，研究者试图了解流动经历对流动人口结婚行为的影响。

表3-7　2013—2015 年流动人口结婚登记地

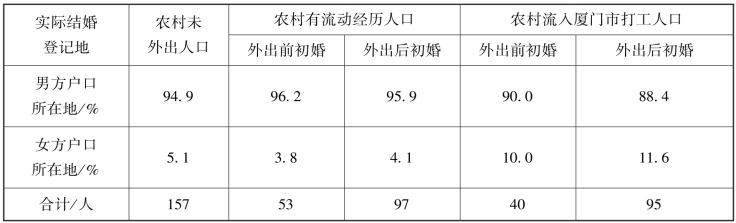
资料来源：厦门大学流动人口婚姻状况调查课题组

★小知识

我国现行的工业企业行业分类就是按产品使用方向、生产工艺及生产工艺流程、使用原材料三个标志，把工业划分为40 个大类、197 个中类和611 个小类，而且对重要的品质标志分组编制成分类目录，如《工业产品目录》《商品分类目录》 等。

2.按数量标志分组

按数量标志分组，也称数量分组。即以反映现象数量特征的标志划分各组。

一般地，对于以定距尺度或定比尺度计量的，采取数量分组。例如，学生按学习成绩、年龄、身高等数量标志分组；企业按销售额、职工人数、计划完成程度等数量标志进行分组。按考试成绩分组，划分出55 ～65 分这么一组显然是不合适的。

另外，数量分组又可以分成单项式分组和组距式分组。

（1）单项式分组。单项式分组就是用一个变量值作为一组。例如，某社区家庭户以其生育子女数分组，可分为0 个、1 个、2 个、3 个4 组，见表3-8。单项式分组一般适用于离散型变量，且适用于变量值较少的情况，组数太多不便于观察数据分布的特征和规律。离散型变量是指所描述对象的变量值可以按一定次序一一列举的数量变量。

表3-8　某社区家庭户拥有孩子数情况表

（2）组距式分组。组距式分组就是将变量值依次划分为几段区间，一段区间表现为“从……到……”距离，把一段区间内的所有变量值归为一组。区间的距离就是组距。其适用于连续型变量或者变量值较多的离散型变量。

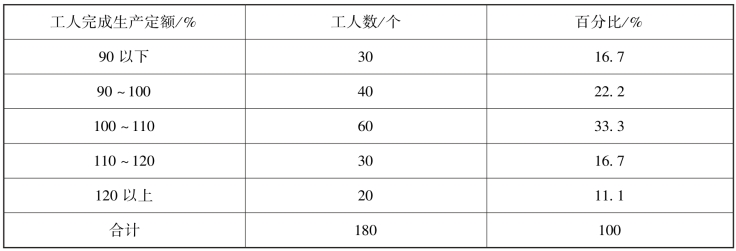
①组距式分组的分类。各组包含许多变量值，每一组变量值中，最小值为下限，最大值为上限，组距是上下限的距离。凡是上下组的组限不相连的，称为间断组距式分组。例如，某社区家庭户以其人口数分组，可分为0 ～1 个、2 ～3 个、4 ～5 个、6 个以上4 组，见表3-9。凡是上下组的组限相连的，称为连续组距式分组。例如，工厂工人完成生产定额情况，分为90% 以下、90% ～100%、100% ～110%、110% ～120%、120% 以上五组，见表3-10。

表3-9　某社区家庭户人口数情况表

表3-10　某工厂工人完成生产定额情况表

(www.daowen.com)

间断组距式分组适用于离散型变量，连续组距式分组适用于连续型变量。这一区别的原因是离散型变量和连续型变量的特点不同，以及统计分组的“穷尽、互斥”原则。连续型变量的可能取值无法一一列举出来，换句话说，在任何两个数值之间都存在无穷多的其他数值，如果采用间距式分组，各组的组限不相连，很有可能遗漏各组限之间的变量值。也就是说，如果我们把工厂工人完成生产定额的组限定为89%以下、90%～99%、100%～109%、110%～119%、120%以上这样五组，满足了“互斥”原则，但是如果某一工人完成生产定额的99.5%，应该归在哪一组呢，显然在以上的分组情况下，这位工人将无组可归，我们就无法满足“穷尽”原则。为了遵守“穷尽”原则，连续型变量在分组时必须选择相连的组限，见表3-10。那么，这样是否违背了互斥原则呢？若某工人恰巧完成生产额的90%，应该分在哪一组呢？为了解决这个问题，统计学规定，相邻两组的上下限应用同一变量值表示，即相邻两组的上下限必须重叠。一般应把重叠的数值归入下限的那一组，这叫作“上组限不在组内”原则。有了这一原则作为补充，上面提出的问题就迎刃而解，90%分在90% ～100%这一组，100%分在100% ～110%这一组，以此类推。

根据各组距是否相等，把组距式分组分为等距分组和异距分组。等距分组就是变量值在各组保持相等的距离，表3-9 和表3-10 都属于等距分组。凡是变量值分布比较均匀的情况，一般可采取等距分组。等距分组便于操作和绘制统计图。异距分组就是各组组距不全相等，见表3-11。

表3-11　某地区人口年龄分布情况

一般地，异距分组适用于以下几种场合：一是变量值分布很不均匀的场合。如果采取等距分组，组距大了，很多变量值都集中到某一两个组，总体的内部结构显现不出来；组距小了，一些组的单位数很少。故此在变量值分布存在明显偏斜的情况下，采用异距分组。例如，人口总体的年龄分布，考虑到80 岁以上的高寿者在总人口中所占比例极小，所以80 岁以下可按5 岁组距分组，80 岁以上的组距就应该扩大。二是变量值相等的量具有不同意义的场合。例如，生命每一年对于不同生命阶段是不一样的，若按年龄分组进行人口的生命阶段研究，应采用异距分组，见表3-11。三是变量值按一定比例发展变化的场合。例如，钢铁厂高炉按容积（立方米）的异距分组为100 以下、100 ～200、200 ～400、400 ～800、800 ～1 600、1 600 以上，其组距间隔等比为2。

总之，采取等距或异距分组并没有严格的规定，研究者还是应该根据分组标志的特点以及研究的具体需要来确定。

（2）组距式分组中的相关指标。

①组距。在组距式分组中，组距是上下限之间的距离。连续组距分组的组距计算：

对于间断式分组的组距大小的计算，采用如下公式：

连续组距式分组的组距大小，也可根据式（3-2）或式（3-3）求得。

②组数。组距的大小直接关系到组数的多少。组距大，组数就少；组距小，组数就大，两者是此消彼长的关系。在实际分组时，可以按美国学者斯德吉斯（H.A.Sturges）提出的经验公式来确定组数k，即

式中，n 为总体单位数。

可根据全部数据的最大值和最小值及式（3-5）求得的组数来确定组距，即

上述的公式仅供参考，不能生搬硬套。组数和组距的确定应以能够显示数据的分布特征和规律为目的，采取组数的多少应依据所研究数据的特性和研究的目的而确定。

③组中值。上下限之间的中点数值称为组中值，组中值的计算公式为

在计算平均指标或进行其他统计分析时，常以组中值来代表各组变量值的平均水平。当各组变量值均匀分布时，组中值就能较强地代表各组变量值的水平，因此，分组时，应尽可能使组内各单位变量值分布均匀。

④开口组的组距与组中值。在编制组距式变量数列时，使用“……以上”或“……以下”这样不确定组距的组，称为开口组。例如，表3-10 中工人完成计划定额分组中，90%以下和120%以上就是开口组。开口组的组距是近似地以相邻组的组距为本组的组距，如上例，90%以下的组，因相邻组的组距为10%，故第一组可视为80% ～90%，利用式（3-7）计算其组中值为85%；120%以上的组距以邻组的组距l0%为本组组距，视为120% ～130%，利用式（3-9）计算组中值为125%。开口组中值的公式：