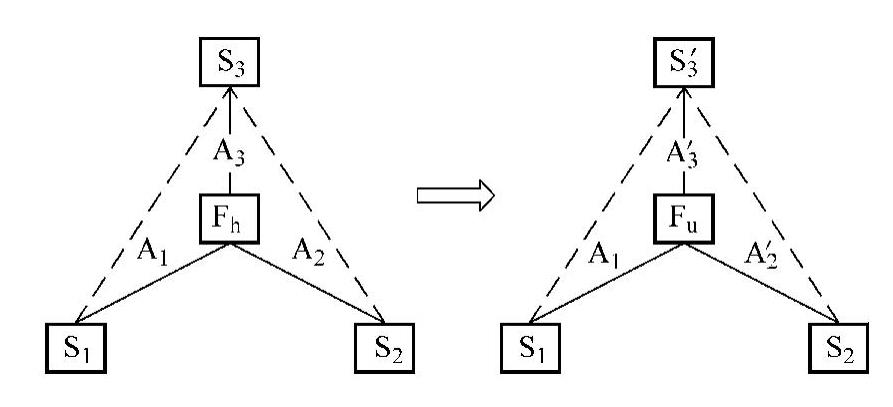
直接对现有系统组件的物质属性进行操作。新属性来自物质S₁或/和S₂内部现有的、未被认识的或尚未被利用的属性（例如A′₂、A′₃等），不必藉由引入外部物质就可获得系统的改进。如图9-17所示。

实例：法兰密封对接。经典的密封结构是在两个法兰端面上加上密封圈，然后用多个螺栓锁紧。其密封程度依赖于法兰边缘上螺栓分布的数量和螺栓拧紧的程度。法兰端面之间的压力P等同于螺栓的压力。过多的螺栓增加了结构的复杂度。如果要减少螺栓的数量同时增加法兰端面之间的压力（提高密封度）似乎是不可能的。但是，如果将某个法兰的端面从垂直于中心线的平面，改成略带一个很小的倾角θ的锥面，如果此时拧紧螺栓，让法兰端面夹角θ趋于零（即轻微变形），则可以成倍地增加P，既减少螺栓数量，同时增加密封度，如图9-18所示。

在该案例中，法兰端面的θ角是法兰的一个新属性，如果用螺栓将其压紧趋零后，还将产生新的法兰属性——因杠杆效应而对端面施加的数倍于螺栓压紧力的压应力P。

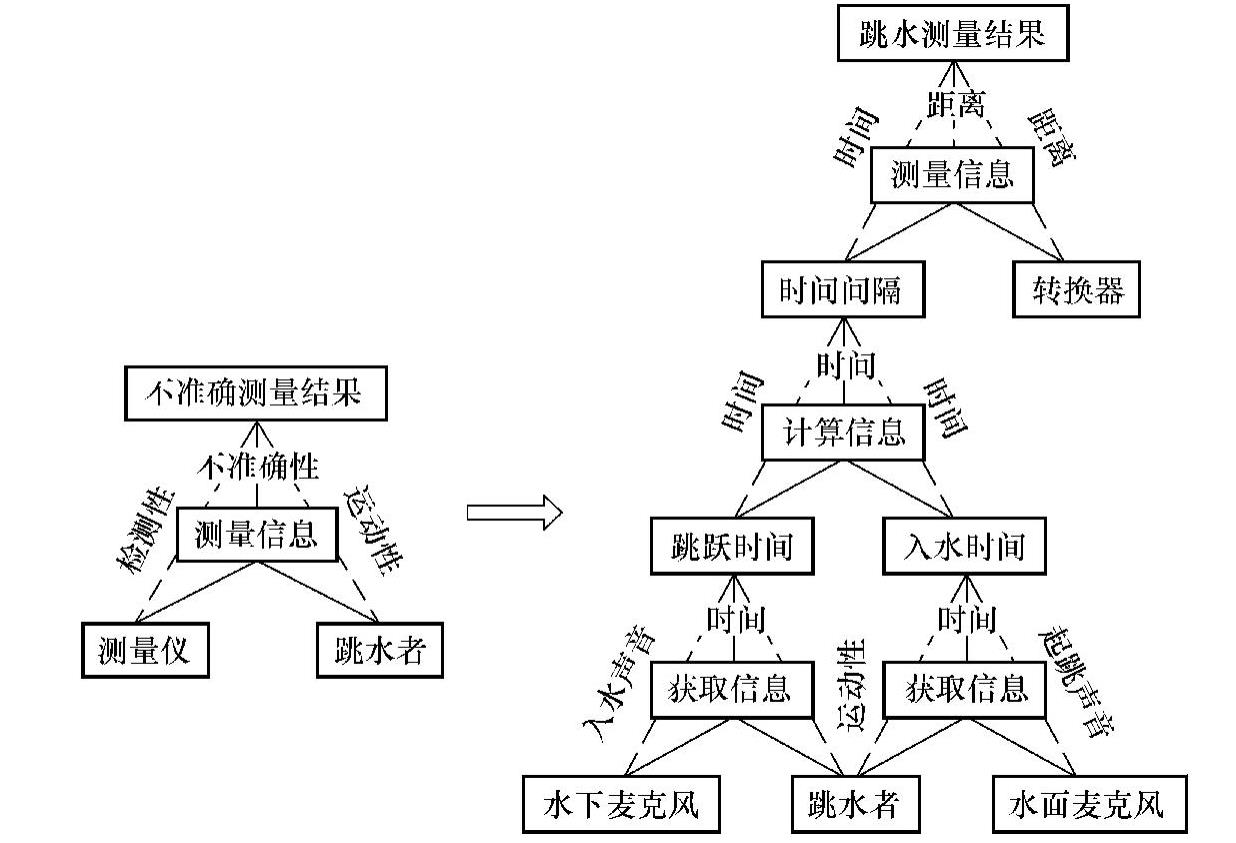
图9-16 测量跳水者的跳跃距离

(www.daowen.com)

图9-17 内调型解题模式

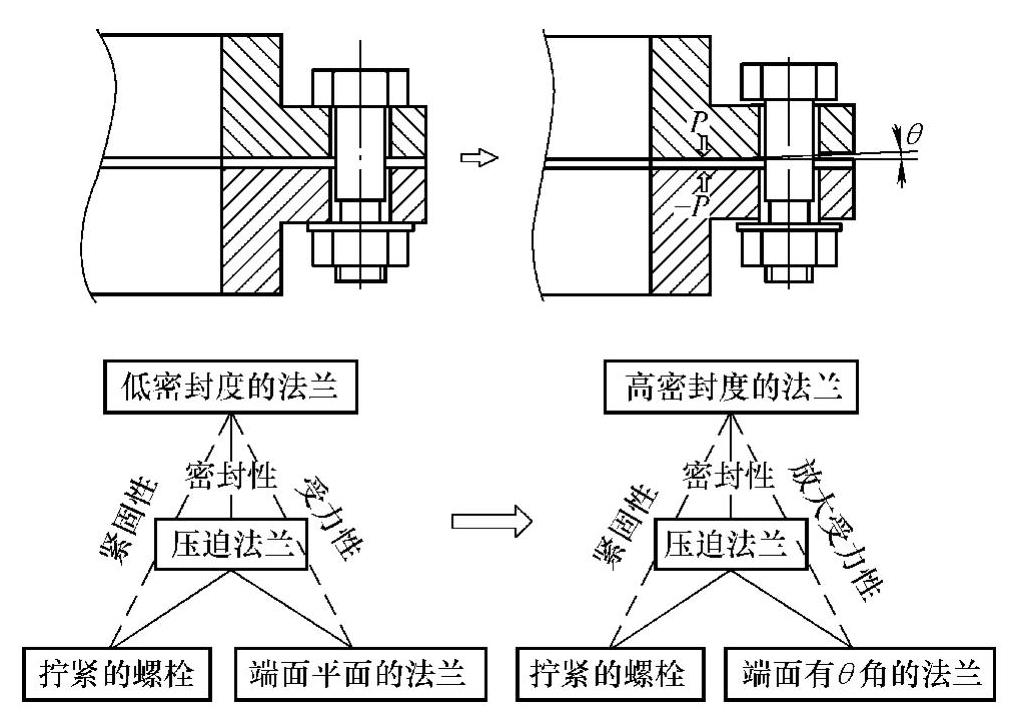
图9-18 法兰端面增加一个θ角的改进设计

内调型解题模式是非常有用的解题模式。它弘扬了TRIZ的基本精神——尽量在有问题的技术系统内部寻找解决问题的资源。既然技术系统中所有的物质（系统组件）的属性都是解题资源，而且一个物质往往是具有多个属性的。因此，有可能并不一定需要从技术系统外部引入物质或场来解决问题。我们只要充分利用系统组件的其他物质属性，或者对系统组件的特征稍微做一点改动并由此获得新属性，就可以利用新属性形成新功能，把问题解决掉。在这一点上，U-TRIZ践行并超越了经典TRIZ中的物场模型的做法。在经典TRIZ物场模型中，解决问题的途径不外乎引入物质，引入场，或者同时引入物质和场。阿奇舒勒虽然一再告诫我们要注意使用技术系统内部的资源，但是在物场模型中，并没有这样的解题模型范式。究其原因，就是因为场仅仅表达了物质的一种属性，更多的物质属性无法通过物场模型表现出来。