（一）负判断的概念及结构

负判断就是否定一个判断的判断，亦即对一个判断进行否定所形成的判断就是负判断。例如：

（1）并非所有违法行为都是犯罪行为。

（2）“只要他有作案时间，他就是案犯”是不对的。

上述例（1）用“并非”否定了肢判断“所有违法行为是犯罪行为”。例（2）中，以“……是不对的”否定了肢判断“只要他有作案时间，他就是案犯”。从上例可以看出，负判断的肢判断可以是一个简单判断，如例（1）；也可以是一个复合判断，如例（2）。

在自然语言中，常用“并非”“不是”“不能说”“是不对的”“不能成立”等表示负判断。其中，典型的联结词是“并非”。负判断的逻辑形式：

并非p

用数理逻辑符号¬（读作“并非”）替代常项“并非”，则负判断的逻辑形式为：

¬p

其中p既可以是一个简单判断，也可以是一个复合判断。

另外，逻辑学通常只是将负判断界定为“否定一个判断的判断”，并没有解释这个被否定的判断是一个真判断还是一个假判断。其实，说透了做这样的解释意义不大。因为，众所周知，逻辑学只不过是人类用以认识客观世界的工具而已，而人类认识世界的目的旨在获取真知而非谬论。故由此可以自得结论：被否定的判断即肢判断为假判断。只有被否定的判断为假判断，才能得到真判断。否则，只能适得其反，只会背离人类认识客观世界的真实意图和真正意义。

（二）负判断的等值判断

由于负判断是否定一个判断的判断，即对肢判断p 的否定。因而，负判断同其肢判断永远是一对矛盾关系。当p真时，其负判断为假；当p假时，其负判断为真。负判断的真假情况，可用真值表表示如下：

表3.8　负判断真值表

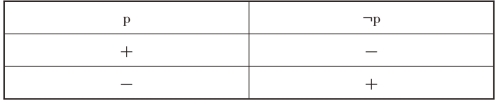
从表中可以看出，如果肢判断真，则负判断假；如果肢判断假，则负判断真；反之亦然。也就是说，负判断¬p与其肢判断p之间，不可同真，也不可同假，是典型的矛盾关系。由此可以得出这样的结论：一个负判断的等值判断是其肢判断的矛盾判断，或者说一个负判断等值于与其肢判断具有矛盾关系的那个判断。逻辑学之所以研究负判断，其根本目的在于通过负判断与其等值判断之间的逻辑关系而获得一个真实判断，以满足人类认识客观世界的需求和目的。

所谓等值，是指两个判断的真假值完全相同。细述之，即为在两个判断中，一个判断真，另一个判断也真，一个判断假，则另一个判断也假，那么这两个判断就是等值判断。以下对前述各种主要的性质判断与复合判断的负判断及其等值判断进行解释。

（三）性质判断的负判断及其等值判断

如前所述，根据性质判断的质和量的结合，可将性质判断分为单称肯定判断、单称否定判断、特称肯定判断、特称否定判断、全称肯定判断和全称否定判断六种。相应地，性质判断的负判断及其等值判断也有六种。

1.单称肯定判断的负判断及其等值判断

前面讲过，同素材的单称肯定判断与单称否定判断是矛盾关系。由此可知，单称肯定判断的负判断等值于同素材的单称否定判断。用逻辑公式表示为：

并非“这个S是P”等值于“这个S不是P”

例如：“并非张某是本案的作案人”等值于“张某不是本案的作案人”。

2.单称否定判断的负判断及其等值判断

根据同素材的单称否定判断与单称肯定判断是矛盾关系，可知单称否定判断的负判断等值于同素材的单称肯定判断。用逻辑公式表示为：

并非“这个S不是P”等值于“这个S是P”

例如：“并非赵某不是本案的作案人”等值于“赵某是本案的作案人”。

3.特称肯定判断的负判断及其等值判断

根据前面讲的同素材的性质判断之间的对当关系，可知特称肯定判断与同素材的全称否定判断是矛盾关系。因此可推出，特称肯定判断的负判断等值于同素材的全称否定判断。用逻辑公式表示为：

并非“有些S是P”等值于“所有S都不是P”

用逻辑符号表示则为：

¬SIP ↔SEP

例如：“并非有些共同犯罪是过失犯罪”等值于“凡共同犯罪都不是过失犯罪”。

4.特称否定判断的负判断及其等值判断

根据前述同素材的性质判断之间的对当关系，可知特称否定判断与全称肯定判断是矛盾关系，故特称否定判断的负判断等值于全称肯定判断。用逻辑公式表示为：

并非“有些S不是P”等值于“所有S都是P”

用逻辑符号表示则为：

¬SOP ↔SAP

例如：“并非有些盗窃罪不是故意犯罪”等值于“所有盗窃罪都是故意犯罪”。

5.全称肯定判断的负判断及其等值判断

根据同素材的性质判断之间的对当关系，全称肯定判断与特称否定判断是矛盾关系，故全称肯定判断的负判断等值于特称否定判断。用逻辑公式表示为：

并非“所有S都是P”等值于“有些S不是P”

用逻辑符号表示则为：

¬SAP ↔SOP

例如：“并非凡成年人都是完全民事行为能力人”等值于“有些成年人不是完全民事行为能力人”。

6.全称否定判断的负判断及其等值判断

根据同素材的性质判断之间的对当关系，全称否定判断与特称肯定判断是矛盾关系，故全称否定判断的负判断等值于特称肯定判断。用逻辑公式表示为：

并非“所有S都不是P”等值于“有些S是P”

用逻辑符号表示则为：

¬SEP ↔SIP

例如：“并非所有民事法律规范都不是强制性规范”等值于“有些民事法律规范是强制性规范”。

（四）复合判断的负判断及其等值判断(www.daowen.com)

前面讲过的复合判断主要有联言判断、相容选言判断、不相容选言判断、充分条件假言判断、必要条件假言判断、充要条件假言判断等。以下对它们各自的负判断及其等值判断分别进行解释。需要说明的是，在分析复合判断的负判断及其等值判断时，务必透彻地理解各种复合判断的真值表，并借助真值表获得复合判断负判断的等值判断。

1.联言判断的负判断及其等值判断

从前述联言判断的真值表可知，联言判断只要有一个联言肢为假，则联言判断就是假的。由此可见，联言判断的负判断的等值判断就是对各联言肢同时加以否定而形成的选言判断。用逻辑公式表示为：

并非“p并且q”等值于“非p或者非q”

用逻辑符号表示为：

¬（p∧q）↔（¬p∨¬q）

例如：“并非他既是教师又是律师”等值于“他或者不是教师或者不是律师”。

现代逻辑运用真值表来表示复合判断的负判断与其等值判断之间的等值关系，联言判断的负判断及等值判断之间的关系可用真值表表示如下：

表3.9　联言判断的负判断及其等值判断关系真值表

从上表可见，¬（p∧q）和（¬p∨¬q）真假情况完全一致，二者等值。

2.相容选言判断的负判断及其等值判断

从前述相容选言判断的真值表可知，相容选言判断只有在“所有选言肢都假”的情况下为假。由此可见，相容选言判断的负判断的等值判断就是对各选言肢同时加以否定而形成的联言判断。用逻辑公式表示为：

并非“p或者q”等值于“非p并且非q”

用逻辑符号表示为：

¬（p∨q）↔（¬p∧¬q）

例如：“并非他或者犯盗窃罪或者犯抢劫罪”等值于“他既不犯盗窃罪，也不犯抢劫罪”。

表3.10　相容选言判断的负判断及其等值判断关系真值表

从上表可见，¬（p∨q）和（¬p∧¬q）真假情况完全一致，二者等值。

3.不相容选言判断的负判断及其等值判断

从前述不相容选言判断的真值表可知，不相容选言判断在“所有选言肢都真”和“所有选言肢都假”这两种情况下为假。由此可见，不相容选言判断的负判断的等值判断就是对各选言肢同时加以肯定或者同时加以否定而形成的多重选言判断。用逻辑公式表示为：并非“要么p，要么q”等值于“[（p并且q）或者（非p并且非q）]”

用逻辑符号表示为：

例如：“并非任某要么是自杀，要么是他杀”等值于“任某既是自杀，也是他杀”或者“任某既不是自杀，也不是他杀”。

因篇幅所限，不相容选言判断的负判断及其等值判断不再用真值表加以表示。

4.充分条件假言判断的负判断及其等值判断

从前述充分条件假言判断的真值表可知，充分条件假言判断在“前件真、后件假”的情况下为假。由此可见，充分条件假言判断的负判断的等值判断就是对其前件加以肯定，同时对其后件加以否定而形成的联言判断。用逻辑公式表示为：

并非“如果p，那么q”等值于“p并且非q”

用逻辑符号表示为：

¬（p→q）↔（p∧¬q）

例如：“并非只要某人有作案动机，那么他就是案犯”等值于“他虽然有作案动机，但他不是案犯”。

表3.11　充分条件假言判断的负判断及其等值判断关系真值表

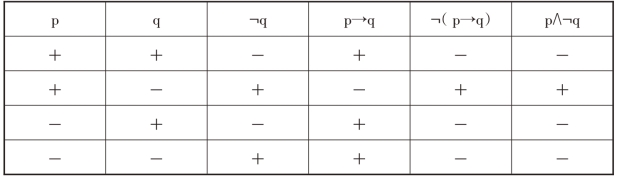
从上表可见，¬（p→q）和（p∧¬q）真假情况完全一致，二者等值。

5.必要条件假言判断的负判断及其等值判断

从前述必要条件假言判断的真值表可知，必要条件假言判断在“前件假、后件真”的情况下为假。由此可见，必要条件假言判断的负判断的等值判断就是对其前件加以否定，同时对其后件加以肯定而形成的联言判断。用逻辑公式表示为：

并非“只有p，才q”等值于“非p并且q”

用逻辑符号表示为：

¬（p←q）↔（¬p∧q）

例如：“并非只有某组织具有法人资格，才能成为民事法律关系的主体”等值于“即使某组织不具有法人资格，它也能成为民事法律关系的主体”。

表3.12　必要条件假言判断的负判断及其等值判断关系真值表

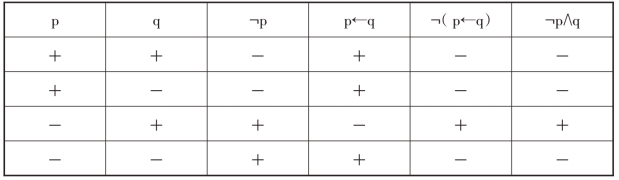
从上表可见，¬（p←q）和（¬p∧q）真假情况完全一致，二者等值。

6.充要条件假言判断的负判断及其等值判断

从前述充要条件假言判断的真值表可知，充要条件假言判断在“前件真、后件假”和“前件假、后件真”的两种情况下为假。由此可见，充要条件假言判断的负判断的等值判断就是对其前件加以肯定同时对其后件加以否定，或者对其前件加以否定同时对其后件加以肯定，而形成的多重选言判断。用逻辑公式表示为：

并非“当且仅当p，才q”等值于[“非p并且q”或者“p并且非q”]

用逻辑符号表示为：

¬（p ↔q）↔[（p∧¬q）∨（¬p∧q）]

例如：“并非当且仅当某人是中华人民共和国公民，他才是中国的纳税人”等值于“某人是中华人民共和国公民但他不是中国的纳税人，或者某人虽不是中华人民共和国公民但他是中国的纳税人”。

因篇幅所限，充要条件假言判断的负判断及其等值判断不再用真值表加以表示。