问题导入

人们在进入建筑工地的时候，必须要戴上安全帽，如图3-3-1所示。这是因为建筑材料处在高处时，会具有一定的能量。一旦它们从高处掉落，这些能量就会释放出来。因此，我们把物体由于处在一定高度而具有的能量叫作重力势能。

图3-3-1　安全帽

在初中我们学习过重力势能的相关知识，重力势能与哪些因素有关呢？下面我们通过一个小实验来回顾一下。

演示实验

重力势能与什么有关

准备两个一样的砝码和一个与砝码大小相等的木块、很轻的小桌、装有细沙的大盒子，将小桌轻放在盒子里。

（1）如图3-3-2甲、乙所示，从不同高度同时由静止释放砝码，观察哪种情况下小桌陷入细沙更深？这说明了什么？

图3-3-2　重力势能与什么有关

（2）如图3-3-2乙、丙所示，从同一高度同时由静止释放砝码和木块，观察哪种情况下小桌陷入细沙更深？这又说明了什么？实验能得出的结论是什么？

1.重力势能

通过上述实验可以看出，重力势能与物体的质量m、所处的位置高度h有关。物理学中，我们把物体的重力势能表示为

Ep=mgh

和其他形式的能一样，重力势能也是标量，单位与功的单位相同，在国际单位制中都是焦耳，从公式中我们也可以看出

1 kg·m/s2=1N·m=1J

我们知道，物体的高度h总是相对于某一水平面而言的，通常把这个水平面的高度取作0。根据公式Ep=mgh可以知道，物体在该平面上的重力势能也是0，因此这样的水平面又叫作零势能参考平面。如图3-3-3所示，以2楼的地面作为参考平面，2楼房间里的物体A具有正的重力势能，1楼的物体B具有负的重力势能。选择的参考平面不同，物体的重力势能是不同的。选择哪个水平面作为参考平面，可以根据研究问题是否方便来定。

图3-3-3　重力势能的相对性

通过前面的学习我们知道，功是能量转换的量度。那么，重力势能的改变是由哪些力做功引起的呢？重力势能的改变和功之间又有什么关系呢？

设有两个质量均为m的小球，从高度为h1处下落到高度为h2处，其中一个小球做自由落体运动，另一个小球在重力和空气阻力的作用下竖直下落，如图3-3-4所示。

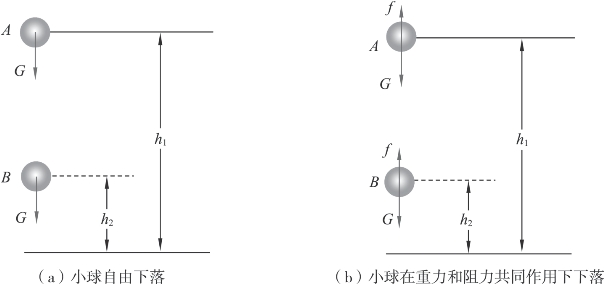
图3-3-4　重力势能的变化与重力做功的关系

两个小球在下落过程中，重力势能的变化为

ΔEp=Ep2-Ep1=mgh2-mgh1

式中，Ep1=mgh1，表示物体在初位置具有的重力势能；Ep2=mgh2，表示物体在末位置具有的重力势能。

小球在下落过程中重力做的功

WG=mgh=mgh1-mgh2

从中我们可以看出，物体重力势能的改变只和物体重力做功有关，与物体是否受到阻力作用或是否有其他力做功没有关系。因此，重力势能的变化和重力做功的关系可以写成

WG=Ep1-Ep2=-ΔEp

当物体从高处运动到低处时，重力做正功，WG＞0，重力势能减少，Ep1＞Ep2；当物体从低处运动到高处时，重力做负功，WG＜0，重力势能增加，Ep1＜Ep2。

做一做

当物体下落的路径不是竖直向下而是沿任意路径时，重力做功还等于重力势能的减少吗？请证明。

我们把由相对位置决定的能叫作势能。除了重力势能外，还有其他形式的势能，如分子势能、电势能、弹性势能等。我们规定，由于物体发生形变而具有的能叫作弹性势能。比如，在射箭比赛中，拉满弦的弯弓在恢复原状时对箭做功，使它发射出去，如图3-3-5所示。

图3-3-5　射箭比赛

2.机械能守恒定律

经过大量的理论研究和实验验证发现，在只有重力做功时，物体的动能和重力势能之间是可以相互转换的，但二者的总和保持不变。我们把这种情况叫作守恒。

下面我们就通过实验来验证一下动能和重力势能的转化和守恒。

探究实验

验证动能和重力势能的转化和守恒

1.进行实验

（1）如图3-3-6所示，让纸带的一端连接重物，另一端穿过打点计时器。

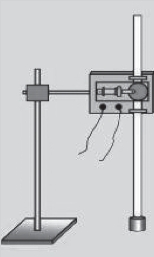
图3-3-6　实验装置

（2）用手提着纸带，让重物靠近打点计时器，接通电源，让重物自由下落，从而在纸带上打下一系列的点。

（3）取下纸带，选择其中一个点作为参考点，规定该点的重力势能为0，算出该点处重物的动能，就是重物下落过程中重力势能和动能的和。

2.记录数据

请自己设计一个实验数据记录表。

3.分析数据

在误差允许范围内，比较在各个点处的重物动能与重力势能的和是否一样。

4.得出结论

在只有重力做功时，物体的动能和重力势能的总和保持不变，即物体的动能和重力势能之间相互转换。

如图3-3-7所示，小球只受重力作用而下落，则根据动能定理有

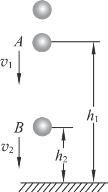
图3-3-7　机械能守恒示意图

由重力做功与重力势能改变的关系可知

联立以上两个式子可得

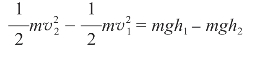
该式说明：重力对小球做了多少功，就有多少重力势能转化为动能。移项后可得(www.daowen.com)

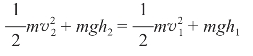
即

Ek2+Ep2=Ek2+Ep1

可见，在只有重力做功的系统中，动能与重力势能可以相互转化，而总的机械能保持不变。

由此可以得出结论：在只有像重力这样的力做功的情况下，物体总的机械能保持不变，但是动能与势能之间可以相互转化。这叫作机械能守恒定律。

【例题】如图3-3-8所示，长l=1m的细绳上端固定，下端系一个质量为m的小球，将小球拉起至细绳与竖直方向成60°角的位置，然后无初速度释放，不计各处阻力，求小球通过最低点时的速度。（取g=10m/s2）

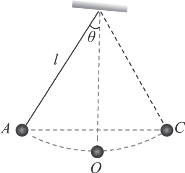
图3-3-8　示意图

分析：在阻力可以忽略的情况下，小球摆动过程中受到重力和细线的拉力。细线的拉力与小球的运动方向垂直，不做功，所以这个过程中只有重力做功，机械能守恒。

小球在最高点只有重力势能，没有动能，计算小球在最高点和最低点重力势能的差值，根据机械能守恒定律就能得出它在最低点的动能，从而算出它在最低点的速度。

解：把最低点的重力势能定为0，以小球在最高点的状态作为初状态，则小球在最高点的重力势能Ep1=mg（l-lcos θ），而动能为0，即Ek1=0。

以小球在最低点的状态作为末状态，势能Ep2=0，而动能表示为。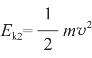

运动过程中只有重力做功，所以机械能守恒，即

Ek2+Ep2=Ek1+Ep1

把各个状态下的动能、势能表达式代入，得

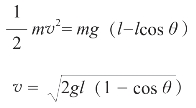
把g=10m/s2，l=1m，θ=60°代入，得

习　题

1.毛泽东的诗词中曾经写过：“一代天骄，成吉思汗，只识弯弓射大雕。”试分析，在成吉思汗弯弓射雕的过程中涉及了哪些能量之间的转化？

2.物体从某一位置运动到另一位置，重力是否一定会做功？

3.质量是3 kg的物体放在距地面1m高的桌面上，物体具有多大的重力势能？

4.质量为50 kg的人爬上高出地面30m的烟囱，他克服重力做了多少功？他的重力势能是增加了还是减少了？改变了多少？（取g=10m/s2）

5.质量为1 kg的物体由静止开始从距地面20m高处自由下落（不计空气阻力），下落到距地面10m处时，它的动能是多少？物体下落到地面时的动能又是多少？

思考与练习

一、填空题

1.一个小孩把6.0 kg的物体沿高0.5m、长2.0m的光滑斜面由底部匀速推到顶端，小孩做功为___________________。若有5.0N的阻力存在，小孩匀速把物体推上去应做____________________功，物体克服阻力做的功为____________________，重力做的功为____________________。（取g=10m/s2）

2.一个光滑斜面长为L，高为h，一质量为m的物体从顶端由静止开始下滑，当所用时间是滑到底端所用时间的一半过程中时，重力做的功为_________，重力做功的平均功率为___________，此时重力做功的瞬时功率为___________________；若以斜面底端为零势能点，则此时物体动能和势能的比是____________________。

二、选择题

1.跳远运动的几个阶段如图3-1所示，则运动员（　）。

图3-1　第1题图

A.助跑阶段机械能不变

B.起跳时机械能为零

C.经过最高点时动能最大

D.经过最高点时重力势能最大

2.小明同学站在匀速上行的自动扶梯上由1楼升到2楼的过程中，下列说法正确的是（　）。

A.小明相对地面是静止的　B.小明的动能大小保持不变

C.小明的机械能总量保持不变　D.自动扶梯把机械能转化为电能

4.一个人把一物体由静止开始举高h，并使其获得一定的速度，则（　）。

A.人对物体做的功等于物体动能和势能增量的和

B.所有外力对物体做的功等于物体动能的增量

C.物体克服重力做的功等于物体势能的增量

D.所有外力对物体做的功等于物体机械能的增量

三、问答题

1.一辆5t的汽车在长100m、高10m的坡路行驶，若汽车受的阻力是自身所受重力的5%，汽车由坡底开到坡顶的过程中速度由10m/s减至5m/s，求汽车的牵引力。

2.一个质量为5 kg的铅球从2m高处由静止释放，砸在松软的地面上，陷入地下25cm后静止，求铅球下陷过程中受到的平均阻力。

实践活动

1.讨论并举例说明平时生活中遇到的有关机械能守恒的例子。

2.自己动手制作遵循机械能守恒定律的小玩具，比一比，看谁做得好。

情境小结

一、功与功率

1.功和功率的定义是什么？

2.当物体移动的方向与力的方向不在一条直线上时，力所做的功怎么算？

3.生活和生产中常见机械功率的大小及其意义是什么？

4.当汽车发动机的功率一定时，牵引力与速度的关系是什么？

二、动能　动能定理

1.动能和动能定理的定义是什么？

2.如何应用动能定理解决生活生产中的问题？

三、势能　机械能守恒定律

1.势能和机械能守恒定律的定义是什么？

2.机械能守恒的条件是什么？

3.如何用机械能守恒定律分析生活中的现象？