对于一些难点问题需要用到多个知识点间叠加，学生对于此类问题在掌握和运用熟练程度不够时，会造成学习和思维的困难，对继续学习造成一定的阻碍，教师教学时要结合习题对一些知识点进行组合，总结规律，形成新的公式，便于学生掌握运用。

如《义务教育教科书　数学　七年级上册》第54页B组复习题第1题。

有理数x1，x2表示在数轴上得到点A1，A2，我们就把x1，x2叫做A1，A2的一维坐标。一般地，称｜x2－x1｜为点A1与点A2之间的距离。如果x1，x2分别取下面各组的值，试求｜x2－x1｜的值。

（1）x1＝5，x2＝2；（2）x1＝2，x2＝－5；（3）x1＝6，x2＝－3；（4）x1＝－3，x2＝－6。

解　（1）x1＝5，x2＝2；A1 A2＝｜x2－x1｜＝｜5－2｜＝3。

（2）x1＝2，x2＝－5；A1 A2＝｜x2－x1｜＝｜－5－2｜＝7。

（3）x1＝6，x2＝－3；A1 A2＝｜x2－x1｜＝｜－3－6｜＝9。

（4）x1＝－3，x2＝－6；A1 A2＝｜x2－x1｜＝｜－6－（－3）｜＝3。

该题的结论适用于坐标轴上两点之间距离的求解，也可用于平行于坐标轴的直线上两点之间距离的求解。如：

例3　已知抛物线y＝2x2－3x－m（m为常数）与x轴交于A，B两点，且AB的长为(www.daowen.com)

（1）求m的值。

（2）若该抛物线的顶点为P，求△APB的面积。

分析：根据题意得知AB的长为只要找到m与线段AB的长之间的关系即可求得m。注意到m为表达式中的常数项，A，B两点在x轴上，根据上题结论AB＝｜x2－x1｜，结合二次函数与x轴交点的横坐标就是相应的一元二次方程的根，再运用韦达定理，可得m与AB的长之间的关系。

解　（1）AB＝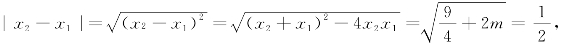

解得m＝－1。

（2）由（1）可得抛物线y＝2x2－3x＋1，则该抛物线的顶点P坐标为

本例的结论还可推广。对于二次函数y＝ax2＋bx＋c（a≠0），与x轴交点的横坐标就是相应的一元二次方程的根，运用韦达定理，可得系数a，b，c与两交点的距离之间的关系为

即　S△APB＝