安徽省滁州市定远县第一初级中学　蒋华榆

中学数学是重要的基础学科，在推进素质教育的过程中肩负着自身的历史重任，对培养和发展中学生素质意义重大。在课堂教学方式、教育形式不断发生变化的今天，只有对每一次的教学流程、教育环节进行不断的反思和总结，及时引导学生对学过的知识和解完的问题进行再一次思考、分析、对比，并找出它们的联系与区别，从而使学生的思维得到延伸发展，激发数学创造性思维。

数学教学离不开解题，而学生的参与度是衡量课堂效率的重要指标之一。我校从2014年3月开始进行“学生讲题活动的实践与研究”的探索与研究，现仍在进行中。从刚开始学生一直面对黑板，不敢面对同学，到现在落落大方地讲题，有时还有质疑、释疑环节，一步步给我许多惊喜。下面我就学生讲题活动中的做法和想法，与大家交流，希望得到各位专家的指导，帮助我在实际教学中不断完善，提升课堂教学效率。

案例1　从甲地到乙地，先是一段平路，然后是一段上坡路。小明骑车从甲地出发，到达乙地后立即原路返回甲地，途中休息了一段时间，假设小明骑车在平路、上坡、下坡时分别保持匀速前进。已知小明骑车上坡的速度比平路上的速度每小时少5 km，下坡的速度比在平路上的速度每小时多5 km。设小明出发xh后，到达离甲地ykm的地方，图1中的折线OABCDE表示y与x之间的函数关系。

（1）小明骑车在平路上的速度为_______km／h；他途中休息了_______h。

（2）求线段AB，BC所表示的y与x之间的函数关系。

（3）如果小明两次经过途中某一地点的时间间隔为0．15 h，那么该地点离甲地多远？

常规讲解思路：

（1）由速度＝路程÷时间可以求出小明在平路上的速度，也可以求出返回的时间，进而得出途中休息的时间。

（2）先由函数图象求出小明到达乙地的时间，并求出点B的坐标和点C的坐标，就可以由待定系数法求出函数表达式。

图　1

（3）小明两次经过途中某一地点的时间间隔只有0．15 h，由题意可以得出这个地点只能在坡路上。设小明第一次经过该地点的时间为t，则第二次经过该地点的时间为（t＋0．15）h，根据该地点与甲地的距离建立方程，求出其解即可。

杨冉同学提出是否可以这样做：

第（1）题同常规讲解思路。

第（2）题利用实际问题中距离＝速度×时间来求。

直线lAB的表达式为　y＝4．5＋10（x－0．3）＝10x＋1．5（0．3≤x≤0．5）；

直线lBC的表达式为　y＝6．5－20（x－0．5）＝－20x＋16．5（0．5＜x≤0．6）。

（3）由常规讲解思路，得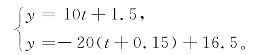解得

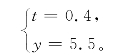
也可以设离乙地距离为s，则s10＋s20＝0．15，解得　s＝1，离甲地的距离为6．5－1＝5．5（km）。

像这样问题的提出对解决题目的本身都起到很好的加深理解的作用，使解题过程更加简洁明了。

案例2　将一个角是36°的等腰三角形分割成两个等腰三角形。

刘睿祖同学提出：所有三角形是否都可以分割成两个等腰三角形？在得到答案是否定的情况下继续提问：满足什么条件，三角形可以分割成两个等腰三角形？

像这样的问题提出超出题目本身的范围，是对题目进行拓展和延伸，拓宽思维的广度和深度，让我很惊讶，同时也很惊喜。不管问题本身如何，我都会给予肯定和引导，鼓励他们坚守自己的猜想，并在班里做适当的宣传，为其他同学树立标杆。现在班里出现一些同学经常和我交流他们的想法，我平时很少这样思考，所以我每次做讲题总结时，都会问学生有没有其他的想法，特别留心讲题小组同学的表情。在课后交流时，也注意询问这样的问题，我也逐渐养成这样的思考习惯。(www.daowen.com)

作为一名教师，由“传道授业解惑”的角色转变为一个鼓励者、促进者，我对这种换位活动进行了全面的总结。

1．调动学生的学习热情

换位教学是一种教学理念，是激发学生学习兴趣的新途径。让学生当“老师”，教师由居高临下变成平等亲近的“学生”，使学生产生好奇心、新鲜感和吸引力，因而会聚精会神地关注“老师”讲课。学生讲题活动就是让学生“先学后教”，要求讲题学生主动思考或动手操作，同时台下同学以审视的目光看待“老师”，“老师”想要充分展示自我，就要付出较多的努力。所谓“功夫在诗外”，要让学生讲题成功，对教师的教学能力提出更高的要求。教师要加强课外指导，指导学生深入研究讲题，加大对题目本身知识的深度、广度的认识，提高解题的技巧，并梳理讲课的条理，组织好语言，同时对所讲问题再一次思考、总结等。给讲题学生多提供独立思考、发散思维的机会。台下的同学也担心“老师”提问自己，如果答不上来会很难堪，同时也想为难“老师”，从而激发学生学习热情，这样能使学生真正参与到学习中去。老师也要组织、协调课堂，以及学生讲题后的总结。从牵着学生一步一步过河，到让学生摸着石头过河，与学生站在对等的地位，与学生交流，充分尊重学生，关注学生成长，了解学生发展中的需求，帮助学生认识自我，建立自信。当学生的学习热情被调动起来，真正的教学就开始了。

2．激励性评价和奖励

每个同学第一次讲题时，都有可能出现各种各样的状况。有的同学始终一直面对黑板，有的同学匆匆讲完解题过程，有的同学板书丢三落四，有的同学甚至出现冷场情况。我的做法是不打断学生的讲题过程，充分尊重学生，给他们时间，让他们完成讲题过程。对于个别学生，在总结时鼓励他，同时列举我自己第一次上课的种种意外情况，让他消除心理障碍，另外会在近期安排他重新讲题，帮助他重拾信心。对在讲题活动中表现好的同学，给予适当的奖励，例如老师语言的夸奖、同学的掌声、做一个“赞”的手势、发一个奖状、奖励一件学习用品等，激发学生强烈的学习愿望，增强学生战胜困难的信心和勇气。

3．引导学生选题

讲题活动到目前阶段，学生在选题时喜欢选大题或难题，似乎是题目越难越能体现自己的水平。而这类题目信息量较大且条件与结论之间有一定的跨度，所以听课的学生一时还梳理不清思路，造成讲题效率较低。我的做法是提前让所有学生拿到题目，预留较充足的时间，同时要求讲题学生充分利用图形的直观性来降低难度，关键步骤要有设问和板书。平时还要引导讲题学生注意选题的难易程度，太难的题目容易挫伤学生的积极性，太简单的题目激发不了学生兴趣。要针对不同层次的学生设置合理的学习目标，防止目标不当，损伤学生的学习积极性。每个学生的学习基础、学习能力、学习兴趣都有差异，有的差异还很大，教师要充分把握好学生的能力，力争做到让参与活动的同学都有所进步，让学生学习适合自己的数学，在讲题活动中提高学习兴趣和学习效率。

4．鼓励学生大胆猜想

学生往往是想到就用，不愿做全面、深入的思考和探究。有时碰巧对了，下次遇到似是而非的情境，就会错得糊里糊涂。如果错了，得不到恰当的引导，创新的火花便会渐渐熄灭。我鼓励学生坚守自己的猜想，告诉他们错误往往是创造的开始。著名数学家、教育家G·波利亚在他的经典名著《数学与猜想》中指出：“在数学领域中，猜想是合理的，值得尊敬的，是负责任的态度。”他给我们的忠告是：“尽早建立猜想，慢些承认它们。”对于提出问题的同学，不管问题本身怎样，都要给予鼓励，希望他们坚持自己的猜想，再慢慢探究、验证修改。好奇心是最好的老师，让我们留给学生更多的自由空间吧。

5．让学生全面成长

许多孩子在家中受到溺爱，“衣来伸手，饭来张口”，自我意识膨胀，但自主、自立、自强意识却较少建立，心智发展也不均衡，而在数学课堂上的讲题活动，可以增强学生的自主、自立、自强意识。

让学生站在主导者的位置去面对多种选择、分析、判断，遴选最佳方案，让学生主体的自发性、主动性完全体现出来。

学生讲课是一次对困难的挑战，是学生必须独立面对的一次挑战。每一个参与讲课的同学，都要积极主动地思考，想办法去克服困难，虽然在这个过程中他们会得到老师的帮助，但老师的帮助是有限的，他们克服困难主要是靠自己，他们要学会将大困难逐步分解成一个个的小困难，并耐心地、勇敢地逐一解决。

观念是行动的灵魂，教师的教学观念对其教学实践活动有着十分重要的影响。随着科技的发展，课堂教学的方式也发生了巨大的变化，在今天，如何激发学生的学习兴趣，激发学生的学习热情变得尤为重要。课堂不再是老师的独舞，学生才是主角，教师是服务者，为学生的学习服务。教师如何促进学生的学习、组织学生讨论、评价和激励学生的学习、激发学生学习的热情和探究的兴趣等都是教师要不断实践和探究的内容。

总之，参与讲课活动的学生在这一过程中，利用自己已有的知识和经验去发现新的问题，探求新的知识，努力地去达到目标，他们更好地认识了自我，体验到学习的乐趣，树立了信心，形成了强烈的荣誉感、责任感。学习热情、学习动机提高了一大步，使学习真正成为一种自觉行为。

美国教育家杜威说过，给孩子一个什么样的教育，就意味着给孩子什么样的生活。

参考文献

［1］中华人民共和国教育部．义务教育数学课程标准（2011年版）［M］．北京：北京师范大学出版社，2012．

［2］熊惠民．数学思想方法通论［M］．北京：科学出版社，2010：4-6．

［3］吴增生．数学解题指导教学策略初探［J］．中国数学教育（初中版），2012（6）：2-9．

［4］秦培元，刘金玉．“先学后教，当堂训练”：洋思教育的密码［J］．江苏教育研究，2011（1C）：22-24．