投资组合理论认为，若干种证券组成的投资组合，其收益是这些证券收益的加权平均数，但是其风险不是这些证券风险的加权平均风险，投资组合能降低风险。

这里的“证券”是“资产”的代名词，它可以是任何产生现金流的东西，例如一件实物资产或者是一个企业。

＞＞1.建筑施工企业资产组合

两个或两个以上资产所构成的集合，称为资产组合。如果资产组合中的资产均为有价证券，则该资产组合也可称为证券组合。

＞＞2.建筑施工企业资产组合的预期收益率

资产组合的预期收益率就是组成资产组合的各种资产的预期收益率的加权平均数，其权数等于各种资产在组合中所占的价值比例。即：

资产组合的预期收益率E（Rp）＝∑wi×E（Ri）

方程式中，E（Rp）表示资产组合的预期收益率；E（Ri）表示第i项资产的预期收益率；wi表示第i项资产在整个组合中所占的价值比例。

＞＞3.建筑施工企业资产组合风险的度量

（1）两项资产组合的风险。

两项资产组合的收益率的方差满足以下关系式：

式中，σp表示资产组合的标准差，它衡量的是组合的风险；σ1和σ2分别表示组合中两项资产的标准差；w1和w2分别表示组合中两项资产所占的价值比例；ρ1，2反映两项资产收益率的相关程度即两项资产收益率之间相对运动的状态，称为相关系数。理论上，相关系数介于区间［—1，1］内。

当ρ1，2＝1时，表明两项资产的收益率具有完全正相关的关系，即它们的收益率变化方向和变化幅度完全相同，这时，σ2p＝（w1σ1＋w2σ2）2，即σ2p达到最大。由此表明，组合的风险等于组合中各项资产风险的加权平均值，换句话说，当两项资产的收益率完全正相关时，两项资产的风险完全不能互相抵消，所以这样的组合不能降低任何风险。

当ρ1，2＝—1时，表明两项资产的收益率具有完全负相关的关系，即他们的收益率变化方向和变化幅度完全相反。这时，σ2p＝（w1σ1—w2σ2）2，即σ2p达到最小，甚至可能是零。因此，当两项资产的收益率具有完全负相关关系时，两者之间的风险可以充分地相互抵消，甚至完全消除。因而，由这样的资产组成的组合就可以最大限度地抵消风险。

在实际中，两项资产的收益率具有完全正相关和完全负相关的情况几乎是不可能的。绝大多数资产两两之间都具有不完全的相关关系，即相关系数小于1且大于—1（多数情况下大于零）。因此，会有0＜σp＜（w1σ1＋w2σ2），即：资产组合的标准差小于组合中各资产标准差的加权平均，也即资产组合的风险小于组合中各资产风险之加权平均值，因此，资产组合才可以分散风险，但不能完全消除风险。

（2）多项资产组合的风险。

一般来说，随着资产组合中资产个数的增加，资产组合的风险会逐渐降低，当资产的个数增加到一定程度时，资产组合的风险程度将趋于平稳，这时组合风险的降低将非常缓慢直到不再降低。

随着资产组合中资产数目的增加，由方差表示的各资产本身的风险状况对组合风险的影响逐渐减小，乃至最终消失。但由协方差表示的各资产收益率之间相互作用、共同运动所产生的风险并不能随着组合中资产个数的增大而消失，它是始终存在的。

那些只反映资产本身特性，可通过增加组合中资产的数目而最终消除的风险被称为非系统风险。那些反映资产之间相互关系，共同运动，无法最终消除的风险被称为系统风险。

＞＞4.建筑施工企业证券组合的预期报酬率和标准差

（1）预期报酬率。

两种或两种以上证券的组合，其预期报酬率可以直接表示为：

式中，rj是第j种证券的预期报酬率；Aj是第j种证券在全部投资额中的比重；m是组合中的证券种类总数。

（2）标准差与相关性。

证券组合的标准差，并不是单个证券标准差的简单加权平均。证券组合的风险不仅取决于组合内的各证券的风险，还取决于各个证券之间的关系。

【例5—6】假设投资100万元，A和B各占50％。如果A和B完全负相关，即一个变量的增加值永远等于另一个变量的减少值。组合的风险被全部抵消，见表5—5所示。如果A和B完全正相关，即一个变量的增加值永远等于另一个变量的增加值。组合的风险不减少也不扩大，见表5—6所示。

表5-5　完全负相关的证券组合数据

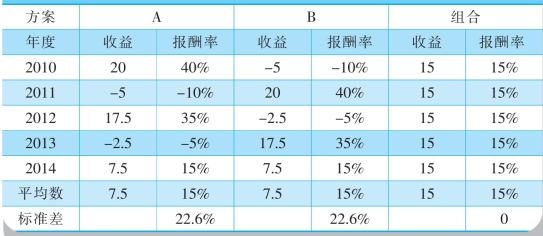
表5-6　完全正相关的证券组合数据

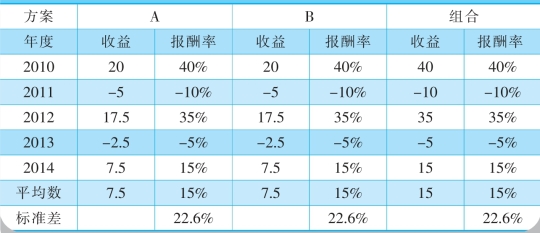
实际上，各种股票之间不可能完全正相关，也不可能完全负相关，所以不同股票的投资组合可以降低风险，但又不能完全消除风险。一般而言，股票的种类越多，风险越小。

＞＞5.建筑施工企业投资组合的风险计量

投资组合的风险不是各证券标准差的简单加权平均数，那么它如何计量呢？投资组合报酬率概率分布的标准差如下：

式中，m是组合内证券种类总数；Aj是第j种证券在投资总额中的比例；Ak是第k种证券在投资总额中的比例；σjk是第j种证券与第k种证券报酬率的协方差。

该公式的含义说明如下：

（1）协方差的计算。

两种证券报酬率的协方差，用来衡量它们之间共同变动的程度：

σjk＝rjkσjσk

式中，rjk是证券j和证券k报酬率之间的预期相关系数；σj是第j种证券的标准差，σk是第k种证券的标准差。

证券j和证券k报酬率概率分布的标准差的计算方法，前面讲述单项证券标准差时已经介绍过。

相关系数总是在—1～1间取值。当相关系数为1时，表示一种证券报酬率的增长总是与另一种证券报酬率的增长成比例，反之亦然；当相关系数为—1时，表示一种证券报酬的增长与另一种证券报酬的减少成比例，反之亦然；当相关系数为0时，表示缺乏相关性，每种证券的报酬率相对于另外的证券的报酬率独立变动。一般而言，多数证券的报酬率趋于同向变动，因此两种证券之间的相关系数多为小于1的正值。

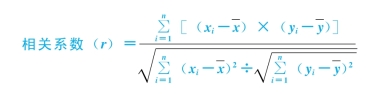
（2）协方差矩阵。

根号内双重的∑符号，表示对所有可能配成组合的协方差，分别乘以两种证券的投资比例，然后求其总和。

例如，当m为3时，所有可能的配对组合的协方差矩阵如下所示：

左上角的组合（1，1）是σ1与σ1之积，即标准差的平方，称为方差，此时，j＝k。从左上角到右下角，共有三种j＝k的组合，在这三种情况下，影响投资组合标准差的是三种证券的方差。当j＝k时，相关系数是1，并且σj×σk变为σ2j。这就是说，对于矩阵对角线位置上的投资组合，其协方差就是各证券自身的方差。(www.daowen.com)

组合σ1，2代表证券1和证券2报酬率之间的协方差，组合σ2，1代表证券2和证券1报酬率的协方差，它们的数值是相同的。这就是说需要计算两次证券1和证券2之间的协方差。对于其他不在对角线上的配对组合的协方差，我们同样计算了两次。

双重求和符号，就是把由各种可能配对组合构成的矩阵中的所有方差项和协方差项加起来。3种证券的组合，一共有9项，由3个方差项和6个协方差项（3个计算了两次的协方差项）组成。

（3）协方差比方差更重要。

该公式表明，影响证券组合的标准差不仅取决于单个证券的标准差，而且还取决于证券之间的协方差。随着证券组合中证券个数的增加，协方差项比方差项越来越重要。这一结论可以通过考察上述矩阵得到证明。例如，在两种证券的组合中，沿着对角线有两个方差项σ1，1和σ2，2，以及两项协方差项σ1，2和σ2，1。对于三种证券的组合，沿着对角线有3个方差项σ1，1、σ2，2、σ3，3以及6个协方差项。在四种证券的组合中，沿着对角线有4项方差项和12项协方差。当组合中证券数量较多时，总方差主要取决于各证券间的协方差。例如，在含有20种证券的组合中，矩阵共有20个方差项和380个协方差项。当一个组合扩大到能够包含所有证券时，只有协方差是重要的，方差项将变得微不足道。因此，充分投资组合的风险，只受证券之间协方差的影响，而与各证券本身的方差无关。

下面举例说明两种证券组合报酬率的期望值和标准差的计算过程。

【例5—7】假设A证券的预期报酬率为10％，标准差是12％。B证券的预期报酬率是18％，标准差是20％。假设等比例投资于两种证券，即各占50％。

该组合的预期报酬率为：

rp＝10％×0.50＋18％×0.50＝14％

如果两种证券的相关系数等于1，没有任何抵消作用，在等比例投资的情况下该组合的标准差等于两种证券各自标准差的简单算术平均数，即16％。

如果两种证券之间的预期相关系数是0.2，组合的标准差会小于加权平均的标准差，其标准差是：

σjj＝12％×12％＝0.0144

σkk＝20％×20％＝0.04

σjk＝0.2×12％×20％＝0.0048

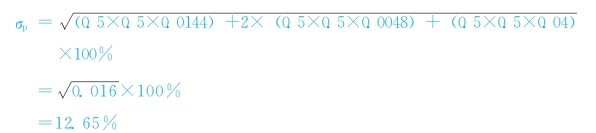
从这个计算过程可以看出：只要两种证券之间的相关系数小于1，证券组合报酬率的标准差就小于各证券报酬率标准差的加权平均数。

＞＞6.建筑施工企业两种证券组合的投资比例与有效集

在例5—7中，两种证券的投资比例是相等的。如果投资比例变化了，投资组合的预期报酬率和标准差也会发生变化。对于这两种证券其他投资比例的组合，计算结果见表5—7。

表5-7　不同投资比例的组合

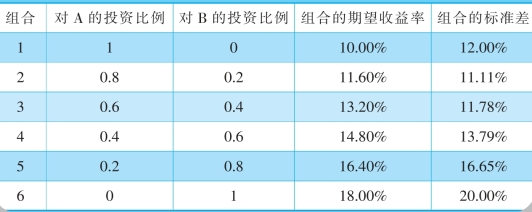
将以上各点描绘在坐标图中，即可得到组合的机会集曲线。

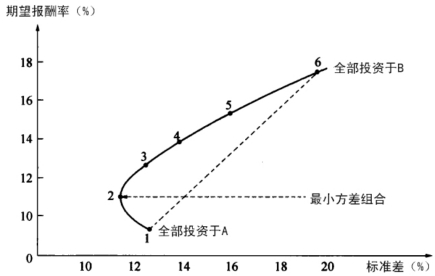
图5—1　投资于两种证券组合的机会集

图5—1描绘出随着对两种证券投资比例的改变，期望报酬率与风险之间的关系。图表中黑点与表5—7中的六种投资组合一一对应。连接这些黑点所形成的曲线称为机会集，它反映出风险与报酬率之间的权衡关系。

该图有几项特征是非常重要的：

（1）它揭示了分散化效应。

比较曲线和以虚线绘制的直线的距离可以判断分散化效应的大小。该直线是由全部投资于A和全部投资于B所对应的两点连接而成。它是当两种证券完全正相关（无分散化效应）时的机会集曲线。曲线则代表相关系数为0.2时的机会集曲线。从曲线和直线之间的距离，我们可以看出本例的风险分散效果是相当显著的。投资组合的抵消风险的效应可以通过曲线1～2的弯曲看出来。从第1点出发，拿出一部分资金投资于标准差较大的B证券会比将全部资金投资于标准差小的A证券的组合标准差还要小。这种结果与人们的直觉相反，揭示了风险分散化的内在特征。一种证券的未预期变化往往会被另一种证券的反向未预期变化所抵消。尽管从总体上看，这两种证券是同向变化的，抵消效应还是存在的，在图中表现为机会集曲线有一段1～2的弯曲。

（2）它表达了最小方差组合。

曲线最左端的第2点组合被称作最小方差组合，它在持有证券的各种组合中有最小的标准差。本例中，最小方差组合是80％的资金投资于A证券、20％的资金投资于B证券。离开此点，无论增加或减少投资于B证券的比例，都会导致标准差的小幅上升。必须注意的是，机会集曲线向点A左侧凸出的现象并非必然伴随分散化投资发生，它取决于相关系数的大小。

（3）它表达了投资的有效集合。

在只有两种证券的情况下，投资者的所有投资机会只能出现在机会集曲线上，而不会出现在该曲线上方或下方。改变投资比例只会改变组合在机会集曲线上的位置。最小方差组合以下的组合（曲线1～2的部分）是无效的。没有人会打算持有预期报酬率比最小方差组合预期报酬率还低的投资组合，它们比最小方差组合相比不但风险大，而且报酬低。因此，机会集曲线1～2的弯曲部分是无效的，它们与最小方差组合相比不但标准差大（即风险大），而且报酬率也低。本例中，有效集是2～6之间的那段曲线，即从最小方差组合点到最高预期报酬率组合点的那段曲线。

＞＞7.相关性对风险的影响

图5—1中，只列示了相关系数为0.2和1的机会集曲线，如果增加一条相关系数为0.5的机会集曲线，就成为图5—2。

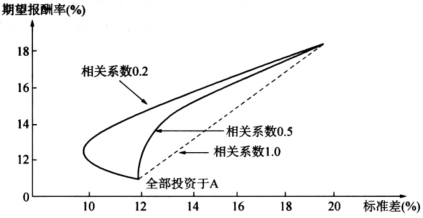
图5—2　不同相关系数情况下的两种证券组合的机会集

从图5—2中可以看到：

（1）相关系数为0.5的机会集曲线与完全正相关的直线的距离缩小了，并且没有向点1左侧凸出的现象。

（2）最小方差组合是100％投资于A证券。

将任何比例的资金投资于B证券，所形成的投资组合的方差都会高于将全部资金投资于风险较低的A证券的方差。因此，新的有效边界就是整个机会集。

（3）证券报酬率的相关系数越小，机会集曲线就越弯曲，风险分散化效应也就越强。

证券报酬率之间的相关性越高，风险分散化效应就越弱。完全正相关的投资组合，不具有风险分散化效应，其机会集是一条直线。

＞＞8.多种证券组合的风险和报酬

对于两种以上证券构成的组合，以上原理同样适用。值得注意的是，多种证券组合的机会集不同于两种证券的机会集。两种证券的所有可能组合都落在一条曲线上，而两种以上证券的所有可能组合会落在一个平面中，见图5—3的阴影部分所示。这个机会集反映了投资者所有可能的投资组合，图中阴影部分中的每一点都与一种可能的投资组合相对应。随着可供投资的证券数量增加，所有可能的投资组合数量将呈几何级数上升。

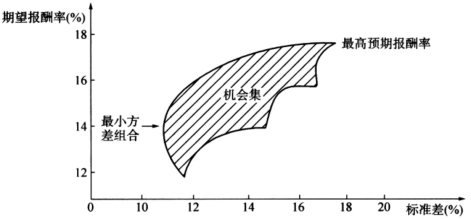
图5—3　机会集举例

最小方差组合是图5—3最左端的点，它具有最小组合标准差。多种证券组合的机会集外缘有一段向后弯曲，这与两种证券组合中的现象类似：不同证券报酬率相互抵消，产生风险分散化效应。

在图5—3中以粗线描出的部分，称为有效集或有效边界，它位于机会集的顶部，从最小方差组合点起到最高预期报酬率点止。投资者应在有效集上寻找投资组合。有效集以外的投资组合与有效边界上的组合相比，有三种情况：

相同的标准差和较低的期望报酬率；

相同的期望报酬率和较高的标准差；

较低报酬率和较高的标准差。

这些投资组合都是无效的。如果你的投资组合是无效的，可以通过改变投资比例转换到有效边界上的某个组合，以达到提高期望报酬率而不增加风险，或者降低风险而不降低期望报酬率，或者得到一个既提高期望报酬率又降低风险的组合。