＞＞1.风险的概念

最简单的定义是：“风险是发生财务损失的可能性”。发生损失的可能性越大，风险越大。它可以用不同结果出现的概率来描述。结果可能是好的，也可能是坏的，坏结果出现的概率越大，就认为风险越大。这个定义非常接近日常生活中使用的普通概念，主要强调风险可能带来的损失，与危险的含义类似。

在对风险进行深入研究以后人们发现，风险不仅可以带来超出预期的损失，也可能带来超出预期的收益。于是，出现了一个更正式的定义：“风险是预期结果的不确定性”。风险不仅包括负面效应的不确定性，还包括正面效应的不确定性。风险的新概念，反映了人们对财务现象更深刻的认识，也就是危险与机会并存。

在投资组合理论出现之后，人们认识到投资多样化可以降低风险。当增加投资组合中资产的种类时，组合的风险将不断降低，而收益仍然是个别资产的加权平均值。当投资组合中的资产多样化到一定程度后，特殊风险可以被忽略，而只关心系统风险。系统风险是没有有效的方法可以消除的，影响所有资产的风险，它来自于整个经济系统影响建筑施工企业经营的普遍因素。投资者必须承担系统风险并可以获得相应的投资回报。在充分组合的情况下，单个资产的风险对于决策是没有用的，投资者关注的只是投资组合的风险；特殊风险与决策是不相关的，相关的只是系统风险。在投资组合理论出现以后，风险是指投资组合的系统风险，既不是指单个资产的风险，也不是指投资组合的全部风险。

在资本资产定价理论出现以后，单项资产的系统风险计量问题得到解决。如果投资者选择一项资产并把它加入已有的投资组合中，那么该资产的风险完全取决于它如何影响投资组合收益的波动性。因此，一项资产最佳的风险度量，是其收益率变化对市场投资组合收益率变化的敏感程度，或者说是一项资产对投资组合风险的贡献。在这以后，投资风险被定义为资产对投资组合风险的贡献，或者说是指该资产收益率与市场组合收益率之间的相关性。衡量这种相关性的指标，被称为β系数。

理解风险概念及其演进时，不要忘记财务管理创造“风险”这一专业概念的目的。不断精确定义风险概念是为了明确风险和收益之间的权衡关系，并在此基础上给风险定价。因此，风险概念的演进，实际上是逐步明确什么是与收益相关的风险，与收益相关的风险才是财务管理中所说的风险。

在使用风险概念时，不要混淆投资对象本身固有的风险和投资人需要承担的风险。投资对象是指一项资产，在资本市场理论中经常用“证券”一词代表任何投资对象。投资对象的风险具有客观性。例如，无论建筑施工企业还是个人，投资于国库券其收益的不确定性较小，而投资于股票则收益的不确定性大得多。这种不确定性是客观存在的，不以投资者的意志为转移。因此，我们才可以用客观尺度来计量投资对象的风险。投资者是通过投资获取收益并承担风险的人，他可以是任何单位或个人。财务管理主要研究建筑施工企业投资。一个企业可以投资一项资产，也可以投资于多项资产。由于投资分散化可以降低风险，作为投资者的建筑施工企业，承担的风险可能会小于建筑施工企业单项资产的风险。一个股东可以投资于一个企业，也可以投资于多个企业。由于投资分散化可以降低风险，作为股东个人所承担的风险可能会小于他投资的各个企业的风险。投资人是否去冒风险及冒多大风险，是可以选择的，是主观决定的。在什么时间、投资于什么样的资产，各投资多少，风险是不一样的。

＞＞2.建筑施工企业资产的风险及其衡量

资产的风险是资产收益率的不确定性，其大小可用资产收益率的离散程度来衡量。离散程度是指资产收益率的各种可能结果与预期收益率的偏差。

衡量风险的指标主要有收益率的方差、标准差和标准离差率等。（1）收益率的方差（σ2）。

收益率方差是用来表示某资产收益率的各种可能结果与其期望值之间的离散程度的一个指标，其计算公式为：

这里E（R）表示资产的预期收益率，可用公式E（R）＝×Ri来计算；Pi是第i种可能情况发生的概率；Ri是在第i种可能情况下该资产的收益率。

（2）收益率的标准差（σ）。

收益率标准差是反映某些资产收益率的各种可能结果对其期望值的偏离程度的一个指标。它等于方差的开方。

其计算公式为：

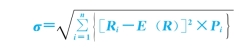
标准差和方差都是以绝对数衡量某资产的全部风险，在预期收益率（即收益率的期望值）相同的情况下，标准差或方差越大，风险越大；相反，在预期收益率相同的情况下标准差或方差越小，风险也越小。由于标准差或方差指标衡量的是风险的绝对大小，因而不适用于比较具有不同的预期收益率的资产的风险。

（3）收益率的标准离差率（V）。

标准离差率是收益率的标准差与期望值之比，也可以称为变异系数。其计算公式为：

V＝σ÷E（R）

标准离差率以相对数衡量资产的全部风险的大小，它表示每单位预期收益所包含的风险，即每一元预期收益所承担的风险的大小。一般情况下，标准离差率越大，资产的相对风险越大；相反，标准离差率越小，相对风险越小。标准离差率可以用来比较具有不同预期收益率的资产的风险。

当不知道或者很难估计未来收益率发生的概率以及未来收益率的可能值时，可以利用收益率的历史数据去近似地估算预期收益率以及其标准差。其中预期收益率可以利用预期收益率的估算方法如算术平均法等来计算，标准差可以利用下列统计中的公式进行估算：(www.daowen.com)

式中，Ri表示数据样本中各期的收益率的历史数据；R是各历史数据的算术平均值；n表示样本中历史数据的个数。

【例5—4】假定甲、乙两项资产的历史收益率的有关资料如表5—2所示。

表5-2　甲、乙两项资产的历史收益率

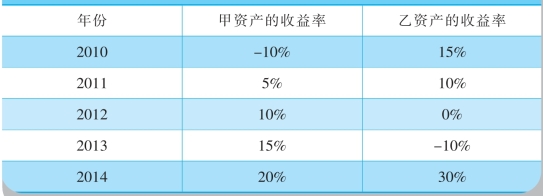
要求：

①估算两项资产的预期收益率；

②估算两项资产的标准差；

③估算两项资产的标准离差率。

解答：

①甲资产的预期收益率＝（—10％＋5％＋10％＋15％＋20％）÷5＝8％

乙资产的预期收益率＝（15％＋10％＋0—10％＋30％）÷5＝9％

②甲资产的标准差：

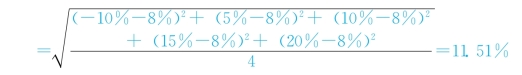
乙资产的标准差：

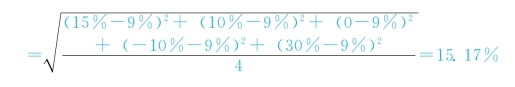
③甲资产标准离差率＝11.51％÷8％＝1.44

乙资产标准离差率＝15.17％÷9％＝1.69

资产的风险尽管可以用历史数据去估算，但由于不同资产的风险受其资产特性的影响较大，另外由于环境因素的多变、管理人员估计技术的限制等，均造成估计的结果往往不够可靠、不够准确。因此，在估计某项资产风险大小时，通常会综合采用各种定量方法，并结合管理人员的经验等判断得出。

＞＞3.建筑施工企业风险控制对策

风险控制对策如表5—3所述：

表5-3　风险控制对策