时间数列的长期趋势是就一个较长的时期而言的，一般来说，分析长期趋势所选的时期越长越好。对长期趋势的测定和分析，是时间数列的重要工作，其主要目的有三个：一是为了认清现象随时间发展变化的趋势和规律性；二是为了对现象未来的发展趋势做出预测；三是为时间数列中剔除长期趋势成分，以便分解出其他类型的影响因素。

长期趋势分析就是采用适当的方法对时间数列进行修匀，使修匀后的数列排除季节变动、循环变动和不规则变动的影响，显示出现象变动的基本趋势，以便认识和掌握现象发展的变化规律，对未来的状况进行预测和分析。

长期趋势分析有线性趋势分析和非线性趋势分析。

1.线性趋势分析

线性趋势分析是现象随时间的推移而呈现出的稳定增长或下降的线性变化规律。线性趋势的分析方法有很多，线性趋势分析的测定方法有时距扩大法、移动平均法、指数平滑法和线性模型法等。这里介绍几种常用方法。

（1）时距扩大法

时距扩大法是测定长期趋势最原始、最简单的方法。它是将原始时间数列中较小时距的若干个数据加以合并，得到较大时距单位的数据。当原时间数列中各指标数值上下波动，使现象变化规律表现不明显时，可通过扩大数列时间间隔来抵消较小时距数据所受到的偶然因素的影响，以反映现象发展的长期趋势。

【例8-17】根据表8-13的数据，用时距扩大法分析某商场2019年销售额的长期趋势。

表8-13　某商场2019年各月销售额

从表8-13所给资料可以看出，该商场2019年各月销售额有高有低，但总的来说是增长的。本例将以月为时距的时间数列合并为以季为时距的时间数列，结果如表8-14所示。原时间数列中不能很好地观察出长期趋势，而扩大时间间距后的新时间数列可以明显地看出该商场的销售额所呈现的长期趋势（增长趋势）。

表8-14　据时距扩大法计算的某商场2019年各季销售额的长期趋势

时距扩大法的优点是简便直观。但是它的缺点也很突出，扩大间距后形成的新时间数列比原数列的数据少，信息大量流失，不便于进一步分析。

（2）移动平均法

移动平均法是对时距扩大法的一种改良。它是采取逐期递推移动的方法对原数列按一定时距扩大，得到一系列扩大时距的平均数。它的原理和时距扩大法类似，通过扩大时距来消除时间数列中的不规则变动和其他变动，以揭示时间数列的长期趋势。移动平均法较时距扩大法的优点在于其可以保留更多的数据信息，对原时间数列的波动起到一定的修匀作用。移动平均法的具体使用步骤如下：

第一步，扩大原时间数列的时间间隔，选定一定的时距项数N。

第二步，采用递推移动的方法对原数列依次移动N项并计算一系列序时平均数。

【例8-18】如表8-15所示，为某钢铁企业2010—2019年钢材产量及其3项移动平均和4项移动平均的计算结果。

表8-15　某钢铁企业2010—2019年钢材产量及其3项移动平均和4项移动平均的计算结果

在3项移动平均中

4项移动平均与3项移动平均不同，4项移动平均要求移动两次，但第一次移动的趋势值也是按照上述方法计算，即

然后，再对以上计算出的趋势值进行2项移动平均得到某时间点趋势值，即

从上例中可以看出，移动平均法具有以下特点：

1）时距项数越大，对时间数列的修匀效果越强。3项移动平均的波动明显小于原数列，一些小波动仍然存在；4项移动平均进一步削弱了波动，时间数列持续上升的长期趋势表现较为明显。

2）当移动平均的时距项数N为奇数时，只需一次移动平均，其移动平均值作为移动平均项中间时期的趋势代表值；当移动平均的时距项数N为偶数时，移动平均值代表的是偶数移动项的中间位置水平，无法对正某一时期，所以需要依次将相邻两项再次移动平均，如此才能使平均对正某一时期值。第二次移动平均称为移正平均，也称中心化的移动平均数。

3）N的选择要考虑周期性波动的周期长短，平均时距N应与周期长度一致。当时间数列包含季节变动时，移动平均的时距项数N应与季节变动长度一致，一般为4个季度或12个月。

4）移动平均以后，其数列的项数较原数列少。当原数列的项数为N项时，移动N项，移动后的新数列项数为N-（n-1）=N-n+1项，比原序列项数减少n-1项。

5）虽然移动项数越多，修匀效果越好，但是移动项数过多会造成数据丢失增加。所以，应综合地考虑以上几个特点来选择合适的移动平均时距项数。

（3）指数平滑法

指数平滑法把过去时间数列值的加权平均数作为趋势值，它是加权移动平均法的一种特殊情形。其基本形式是根据本期的实际值Yt和本期的趋势值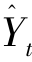分别以不同权数α和1-α计算加权平均数来作为下期的趋势值。观测时间越远，其权数越小；观测时间越近，其权数越大。指数平滑法的基本模型为

式中，表示时间数列第t+1期的趋势值；Yt表示时间数列第t期的实际值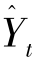；表示时间列第t期的趋势值；α表示平滑系数（0<α<1）。

利用指数平滑法模型进行预测，从基本模型中可以看出，只需一个t期的实际值Yt、一个t期的趋势值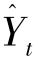和一个α值。利用指数平滑法模型进行预测时，所用数据量和计算量都很少，这是移动平均法所不能及的。

指数平滑法可分为一次指数平滑法和多次指数平滑法。本节介绍一次指数平滑法的应用。

【例8-19】某公司2019年前八个月的销售额见表8-16，试用指数平滑法进行长期趋势分析。已知1月份预测值为150.8万元，分别取α=0.2和α=0.8。预测结果见表8-16。

表8-16　某公司2019年前八个月的销售额

一次指数平滑法比较简单，但也有问题，由例8-19可看出，α值和初始值的确定是关键，它们直接影响趋势值误差的大小。

在应用指数平滑法时，选择合适的平滑系数是非常重要的。选择是否得当，直接影响预测结果。α值越大，说明预测越依赖于近期信息；α值越小，则表示预测越依赖于历史信息。选择平滑系数α值时，一个总的原则是使预测值与实际观察值之间的误差最小。理论上，α值取[0，1]的任意数据均可。具体如何选择，则要视时间数列的变化趋势决定。

1）当时间数列呈较稳定的水平趋势时，α应取得小一些，如从[0.1，0.3]选取，以减小修正幅度。这时各期观察值的权数差别不会太大，且预测模型能包含更长时间数列的信息。

2）当时间数列波动较大时，宜选择居中的α值，如从[0.3，0.5]选取。这时，模型能迅速根据当前的信息对预测进行大幅度修正。

3）当时间数列波动很大，呈现明显的上升或下降趋势时，α值应取得大一些，如从[0.6，0.8]选取。这样能使预测模型灵敏度更高，以迅速跟上实际数据的变化。

4）在实际预测中，可取几个α值进行试算，比较预测误差，最终选择误差最小的那个α值。

初始值的确定：如果时间数列观察期N大于15，则经过长期平滑链的推算，初始值的影响变得相对较小，为了简便起见，可用第一期水平作为初始值。但是如果N小于15，则初始值的影响较大，可以选用最初几期的平均数作为初始值。

（4）线性模型法

线性模型法也称直线趋势方程拟合法，就是根据时间数列发展形态的特点，选择一种合适的数学方程式，进而以t代表时间，以y代表实际观测值，然后依据此方程来分析长期趋势的方法。

要拟合一条符合上述要求的趋势线，最合理的方法就是最小二乘法（最小平方法），它既适用于直线拟合，也适用于曲线拟合。直线趋势方程为

式中，yc表示时间数列的趋势值；t表示时间；a表示直线趋势方程的起点值；b表示直线趋势方程的斜率，即t每变动一个单位时长期趋势值增加（或减少）的数值。

下面利用最小二乘法来求解参数a、b。

令，为使其最小，需对a和b求偏导并令偏导数等于0，整理得

解得

式中，n表示时间的项数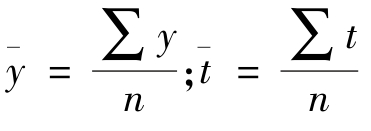；；其他符号所代表的意义同前。

【例8-20】用某省2015—2019年“十一黄金周”国内人均旅行消费数据建立直线趋势方程并进行长期趋势分析，如表8-17所示。

表8-17　某省2015—2019年“十一黄金周”国内人均旅行消费数据最小二乘法计算表

由表8-17得

代入公式得

从而求得直线趋势方程为

把各t值代入上式，便可求得相对应的趋势值yc，详见表8-17。这里需要指出的是，表8-17“十一黄金周”国内人均旅行消费数据用直线趋势拟合，是因为各年的逐期增减量大体相当，具备了直线型时间数列的特征。

在对时间数列按最小二乘法进行直线趋势拟合运算时，为使计算简便，可以用坐标移位法将原点O移到时间数列的中间项，使∑t=0（即简捷法）。当时间数列的项数N为奇数时，可以取中间项的时间顺序号为0，中间项以前的时间序号从中间往前依次为-1，-2，-3，…，中间项以后的时间序号从中间往后依次为1，2，3，…；当时间数列的项数N为偶数时，将最中间的两项分别设为-1，1，然后从中间到两边，以前各期依次取-3，-5，-7，…，以后各期依次取3，5，7，…。这样，求解公式便可简化为

用简捷法公式计算的直线趋势方程和标准方程组求出的方程实际上是同一条趋势线，所不同的是原点的位置，原点改变后的趋势值和原点改变前的趋势值是相等的。

同一资料按简捷法公式计算，有

即

将各t值代入上式，便可求得各年的趋势值yc，详见表8-18。

利用最小二乘法对原数列进行长期趋势测定时，通过趋势值来修匀原数列，会得到比较接近原值的趋势值。此外，还可利用所求直线趋势方程对近期的数列做出预测。

例如，根据表8-17求出直线趋势方程，并将t=6代入，便能预测该省2020年的国内人均旅行消费数据，即(www.daowen.com)

根据表8-18求出直线趋势方程，并将t=3代入，便能预测该省2020年的国内人均旅行消费数据，即

表8-18　某省2015—2019年“十一黄金周”国内人均旅行消费数据最小二乘法计算表（简捷法）

续表

需要注意的是，这里的直线趋势方程yc=a+bt不涉及变量t与变量y之间的任何因果关系，也没有考虑误差的任何性质，因此它仅仅是一个直线拟合公式。同时还需指出，作为较长期的一种趋势，利用所拟合的数学方程式进行预测时，必须假定影响趋势变化的因素到预测年份仍起作用。上面的例题只是为了说明分析计算的方法，简便起见，一般选用的数据都比较少，实际应用时，应丰富数据以便更好地反映长期趋势。

2.非线性趋势分析

当时间数列各时期的数值随时间而不同，且各时期的变化率或趋势线的斜率有明显变动但又有一定规律性时，现象的长期趋势就不再是线性，而可能是非线性。

现象的非线性趋势的形式多种多样，这里只介绍常见的抛物线型和指数曲线型。

（1）抛物线型

如果时间数列二级增减量（即各期增减量的逐期增减量）大体相同，表明现象变化趋势是一个弯曲的曲线，则可用抛物线方程拟合一条合适的曲线。建立的趋势方程为

方程中有三个待定参数，根据最小二乘法，可得如下标准方程组，即

解此方程组，求出参数a、b、c，就可得到抛物线的趋势方程。

与直线趋势分析一样，抛物线趋势分析也可用简捷法解出参数以建立抛物线的趋势方程。若将原数列的中点移至坐标原点，使∑t=0，则标准方程组可简化为

解此方程组，求出参数a、b、c，也可得到方程。得到抛物线的趋势方程后，即可计算出各个时期的趋势值，进行分析预测。

（2）指数曲线型

当现象发展水平的每期按大体相等的增减速度变化时，时间数列适宜拟合指数曲线。建立的指数曲线趋势方程为

式中，a表示修匀数列的初始水平；b表示单位时间内趋势值的发展速度。

由于指数曲线具有如下特性：

所以，当时间数列的各期数值大致按某一相同比率增减时，可以考虑拟合指数方程。联系常用的复利公式：Pn=P0（1+r）n，令Yt=Pt，a=P0，b=l+r，n=t，则复利公式与指数方程完全一致，可见指数曲线是一种常用的典型趋势线。

为估计参数a、b，可在yc=abt两边同时取对数，即lnY=lna+tlnb，令Y′=lnY，a′=lna，b′=tlnb，可将指数曲线方程转化为直线形式，即

先按照最小二乘法估计出a′和b′，再取反对数得参数a、b的估计值，进而得到指数曲线趋势方程，计算出各个时期的趋势值，进行趋势分析。

3.季节变动分析

季节变动是指一些现象由于受自然条件或经济条件的影响在一个年度内随季节的更替而发生比较有规律的变动。例如，农产品的生产量、某些商品的销售量会因时间的变化而分为农闲农忙、淡季旺季。季节变动往往会给社会生产和人民的经济生活带来一定影响。测定季节变动的意义主要在于通过分析与测定过去的季节变动规律，为当前的经营管理决策提供依据，以避免由于季节变动引起不良影响。分析与测定季节变动规律还可以预测未来，制订计划，以便提前做好合理安排。

根据是否排除长期趋势的影响，测定季节变动的方法可分为两种：一是不排除长期趋势的影响，直接根据原时间数列来测定；二是依据消除长期趋势后的时间数列来测定。前者常用同期平均法，后者常用趋势剔除法。但是不管采用哪种方法，都需要具备连续多年的各月（季）资料，以保证所求的季节比率具有代表性，从而能比较客观地描述现象的季节变动。现将两种测定方法介绍如下。

（1）同期平均法

在现象不存在长期趋势或长期趋势不明显的情况下，一般直接用平均的方法通过消除循环变动和不规则变动来测定季节变动，在统计学中将这种方法称为同期平均法。

这种方法是测定季节变动最简便的方法，其特点是测定季节变动时，不考虑长期趋势的影响。它是以若干年资料数据求出同月（季）的平均水平与全年各月（季）水平，用二者对比得出各月（季）的季节指数以表明季节变动的程度。季节指数是用来刻画数列在一个年度内各月或季的典型季节特征，反映某一月份或季度的数值占全年平均数值的大小。如果现象的发展没有季节变动，则各期的季节指数应等于100％；如果某一月份或季度有明显的季节变化，则各期的季节指数应大于或小于100％。季节变动的程度是根据各季节指数与其平均数（100％）的偏差程度来测定的。

同期平均法的具体步骤如下：

第一步，列表，将各年同月（季）的数值列在同一纵栏内；

第二步，将各年同月（季）数值加总，求出月（季）平均；

第三步，将所有月（季）数值加总，求出总的月（季）平均；

第四步，求季节指数，即S=各月（季）平均/全期各月（季）平均×100％。

【例8-21】某商场某品牌彩色电视机2015—2019年月度销售量资料如表8-19所示，试用同期平均法进行变动分析。

表8-19　某商场某品牌彩色电视机2015—2019年月度销售量

第一步，列表，将各年同月的数值列在同一栏内；

第二步，将各年同月数值加总，求出月平均；

第三步，将所有月数值加总，求出总的月平均，即

第四步：求季节指数，即

从表中数据可知，2月、3月、4月、5月、10月、11月的季节指数均大于100％，是销售的旺季；其他月份的季节指数均小于100％，是销售的淡季。

假设2020年该商场销售的彩色电视电比2019年增加5％，即达到605×（1+5％）=635.25（台）。若要利用季节比率对各月的销售量进行预测，则可先将635.25量除以12，再乘以各月的季节比率求得。例如，1月份预测值=635.25/12×43％=22.76（台）。

同期平均法计算简便，易于理解，但不能消除时间数列所包含的长期趋势和循环波动。因此，当时间数列存在明显的长期趋势时，该方法的季节指数不够准确。当时间数列在剧烈的上升趋势时，年末季节指数明显高于年初的季节指数；当时间数列存在下降趋势时，年末季节指数明显低于年初的季节指数。此时，不宜用同期平均法进行季节变动分析，而应该用趋势剔除法来测定其季节变动。

（2）趋势剔除法

在具有明显的长期趋势变动的数列中，为了测定季节变动，必须先将长期趋势变动因素剔除。假定长期趋势、季节变动、循环变动和不规则变动对数列的影响可以用乘法模型反映。为了精确计算季节指数，首先设法从数列中消除趋势因素（T），然后用平均的方法消除循环变动（S），进而分解出季节变动成分。其具体步骤如下：

第一步，计算移动平均值（季度数据采用4项移动平均，月份数据采用12项移动平均），并将结果进行中心化处理，得到各期的长期趋势值T。

第二步，计算移动平均的比值，即将数列的各观察值除以相应的中心化移动平均值，得到包含循环变动和不规则变动的季节变动指数。

第三步，用平均的方法消除循环变动和不规则变动，计算出各比值的季度（或月份）平均值，即季节指数。

第四步，调整季节指数。各季节指数的平均数应等于1或100％，若根据第三步计算的季节比率的平均值不等于1，则需要进行调整，具体方法是：将第三步中计算的每个季节比率的平均值除以它们的总平均值。

【例8-22】按趋势剔除法计算表8-20中某企业各季销售额的季节指数。

表8-20　某企业各季销售额

首先，利用移动平均法求得长期趋势值T，然后利用公式S×C×I=Y/T计算各季包含了循环变动和不规则变动的季节变动指数，结果如表8-21所示。

表8-21　企业销售额季节指数计算表（一）

续表

其次，利用同期平均法计算销售额的季节指数，消除循环变动和不规则变动。求得的季节指数分别是0.932、0.838、1.093、1.137，如表8-22所示。

表8-22　销售额季节指数计算表（二）

如果上一步求得的四个季节指数的平均数不为1，则还需进行调整，即先求得四个季节指数的总平均数，再用四个季节指数与总平均数的比率作为最后的季节指数。该例题中上一步计算的四个季节指数的平均数已经为1，所以不用再进行调整。

4.循环变动分析

循环变动是指变动周期大于一年、有一定规律的重复变动。循环变动的周期一般超过一年，且没有固定的变动期限或规律，很难事先预知。循环变动各个时期有不同的原因，变动程度也有自己的特点，这和季节变动基于大体相同的原因和相对稳定的周期形成对照，所以不能用测定季节变动的方法来研究循环变动。通常用剩余法来测定循环变动，其基本思想是：对各期资料用长期趋势和季节比率来消除趋势变动和季节变动，得到反映循环变动与不规则变动的数列；然后采用移动平均法消除不规则变动，便可得出反映循环变动程度的各期循环变动系数，即

将C·I数列进行移动平均修匀，修匀后的数列即各期循环变动的系数。

测定循环变动的程度，认识经济波动的某些规律，预测下一个循环变动可能产生的各种影响，以便充分利用有利因素，避免不利因素，这对保持国民经济持续稳定的发展具有重要意义。但是循环变动预测和长期趋势预测不同，循环变动预测属于景气预测，在很大程度上要依靠经济分析，仅对历史资料进行统计处理是不够的。

时间数列趋势分析与预测（上）（下）（教学视频）

知识与能力训练

[1]资料来源：商务部网站。