回归方程是在线性相关条件下，反映两个变量之间一般数量关系的数学模型。根据回归方程，可以由自变量的给定值推算因变量的值。但是，推算出的因变量数值并不是一个精确值，而是一个估计值或理论值，它和实际值是有出入的。例如，前例中的1号企业，生产性固定资产价值为200万元，实际增加值为638万元，而根据回归方程推算出来的增加值只有575万元，二者相差63万元。由此可见，由回归方程进行推算或预测是存在误差的。建立回归方程的主要目的是推算或预测，即根据给定的自变量的数值来推算未知的因变量的数值。这个推算结果的准确程度如何，主要取决于所拟合的回归直线的代表性。故回归直线的代表性和推算结果的准确性是一个问题的两个方面。我们在进行回归分析时，必须弄清这个问题。

1.估计标准误差的意义与计算

估计标准误差是说明使用回归方程推算结果准确程度的分析指标，也是反映回归直线代表性大小的分析指标。估计标准误差和标准差的性质相同，都是说明离散程度的指标。估计标准误差用来说明估计理论值的代表性。若估计标准误差小，则表明回归方程估计准确程度高，代表性大；反之，则估计准确程度低，代表性小。估计标准误差的符号为Sy，其计算公式为

式中，Sy表示估计标准误差；n-2表示自由度。

因在一元线性回归方程中计算a、b两个参数，故失去了两个自由度。

从定义上看，估计标准误差反映了实际观察值y与估计值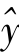之间的平均离差程度。就回归直线来说，这个离差值越小，说明观察点越靠近回归直线，即回归直线的代表性越大；离差值越大，则观察点离回归直线越远，回归直线的代表性越小。

【例7-3】以表7-6所示资料为例，说明估计标准误差的计算方法。

表7-6　某地区8个企业的产品销售额和销售利润

续表(www.daowen.com)

把计算结果代入公式，得

计算结果表明，估计标准误差为4.086 6万元，即对于每一个企业的销售利润来说，其回归估计值的误差有大有小，但平均误差等于4.086 6万元。

2.估计标准误差与相关系数的关系

估计标准误差与相关系数在数量上存在着密切的相关关系，这就从另一个角度说明了相关分析与回归分析之间的关系。二者之间的关系可由下列公式表达，即

式中，r表示相关系数；σy表示因变量数列的标准差；Sy表示估计标准误差。

从上面的计算公式可以看出，r和Sy的变化方向是相反的。r越大，Sy越小，表示相关程度越高，回归直线的代表性越大；r越小，Sy越大，表示相关程度越低，回归直线的代表性越小。

在实际的相关分析中，一般不用这种方法计算相关系数，因为这种计算方法存在两个缺陷。一是需要先求出直线回归方程，计算出估计标准误差，然后才能求得相关系数。从一般的认识程度来看，只有相关关系密切的情况下拟合回归方程才有意义；如果相关关系不密切，那么下一步的计算就没有必要了，因而要求先计算相关系数以判断相关关系的密切程度。二是以这种方法计算出来的结果难以判断是正相关还是负相关。