1.一元线性回归分析及其特点

一元线性回归又称简单直线回归，它是对具有显著相关的两个变量之间数量变化的一般关系进行测定，根据实际测定的数据，拟合一个直线回归方程，用以估计或预测两个变量之间关系的统计方法。它反映的是一个因变量和一个自变量之间的数量变动对应关系。

在回归分析中，一元线性回归分析是应用最广泛的回归分析方法，拟合的数学方程叫一元线性回归方程。

（1）一元线性回归分析应具备的条件

1）现象之间确实存在数量上的相互依存关系。只有当两个变量存在高度密切的相关关系时，所构建的回归模型才有意义，用以进行分析和预测才有价值。

2）现象之间存在直线相关关系。一元线性回归方程在图形上表现为一条直线，因此，只有当两个变量的相关关系表现为直线相关时，所拟合的直线方程才是对客观现象的真实描述，才可用来进行统计分析。如果现象之间的相关关系表现为曲线，却拟合成一条直线，则必然会得出错误的分析结论。在实际工作中，一般是借助散点图来判定现象是否直线相关。

3）具备一定数量的变量观测值。直线回归方程是根据自变量和因变量的样本观测值求得的，因此，变量x和变量y二者应有一定数量的对应观测值，这是构建直线回归方程的依据。如果观测值太少，受随机因素的影响较大，就不易观察出现象之间的变动规律性，所求出的直线回归方程也就没有多大意义。

（2）建立一元线性回归模型

一元线性回归模型的基本形式为

式中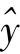，表示因变量y的估计值；x表示自变量；a表示回归直线在y轴上的截距，即当x=0时回归直线与y轴交点到原点的距离。其中，a>0，表示回归直线与y轴的交点在x轴的上方；a<0，表示回归直线与y轴的交点在x轴的下方；a=0，表示回归直线通过原点。b表示回归直线的斜率，也叫回归系数。b的含义是当自变量x每增加一个单位时，因变量y随之变动的平均值。其中，b>0，表示随x增加，y亦增加；b<0，表示随x增加，y减少；b=0，表示回归直线与x轴平行，意为y与x无关。

a与b都是一元线性回归方程的参数。要确定一元线性回归方程，首先需确定回归参数a与b。

经验证明，符合“离差平方和最小”的直线最合适，所以回归参数a与b采用最小二乘法进行确定。设

将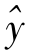=a+bx代入上式，可得

对其求偏导数，可得

经过整理，可得求解参数a、b的公式，即

将两变量的实际观测资料代入上式，即可计算出一元线性回归方程待定参数a与b；然后，将a与b代入一元线性回归方程模型公式，即可求出最合适的直线。(www.daowen.com)

（3）一元线性回归分析的特点

1）在回归分析中，两个变量的关系不是对等的，必须区分开自变量和因变量。关于自变量和因变量的区分，主要根据现象之间的因果关系或分析研究的目的确定。

2）在回归分析中，对于互为因果关系的两个变量x和y，可以建立两个回归方程，一个是y倚x的回归方程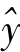=a+bx，x是自变量，y是因变量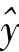，为y的理论值（又称为回归值）；另一个是x倚y的回归方程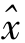=c+dy，y为自变量，x为因变量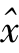，为x的理论值。

3）在回归分析中，自变量是可控变量，因变量是随机变量。

4）在回归分析中，回归系数b的前面有正负号之分。其中，正号（+）表示两变量之间变动的方向相同，即正相关；负号（-）表示两变量之间的变动方向相反，即负相关。

5）在回归分析中，可以根据拟合的回归方程在自变量与因变量之间进行互相推算，并可以对以前缺失的资料进行补充，对以后的资料进行预测。

2.一元线性回归分析的应用

【例7-2】现有10个同类企业的固定资产价值与增加值资料，如表7-5所示，试建立固定资产价值与增加值的一元线性回归方程。

表7-5　一元线性回归方程计算表

将计算表中的有关数据代入公式，可得

将a和b的值代入回归方程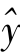=a+bx，可得

该例中，a=395.6万元，表示企业工业增加值的起点值，即式中x等于零时的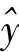值。在相关图上，a表现为回归直线在y轴上的截距；b=0.895 8，称为回归系数，表明固定资产价值每增长1万元，工业增加值平均增加0.895 8万元。在相关图上，b表现为回归直线的斜率。b为正数，表示两现象属于正相关。

根据一元线性回归方程，将各企业的固定资产价值的实际数代入，可以依次推算各企业工业增加值的估计值。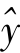

例如，1号企业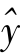=395.6+0.895 8×200=575（万元）。其余各企业的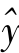值类推，得数已列入表7-5中。