相关表和相关图可以大体说明两个现象是否相关以及相关的类型，但它们的相关关系的密切程度无法表达出来，因此，还应该进一步用统计分析指标来表明相关关系的密切程度。测定变量之间相关关系密切程度比较完善的指标是相关系数。

1.相关系数的意义

相关系数是直线相关条件下，说明两个现象之间相关关系的方向和密切程度的统计分析指标，通常用r表示。

相关系数的计算公式有多种形式，其中最常用的有积差公式和简捷公式。

1）积差公式为

式中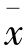，表示x变量数列的算术平均数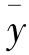；表示y变量数列的算术平均数。

2）简捷公式为

积差公式中，当为除不尽的小数时，计算既麻烦又影响其准确性。因此，在实际问题中，如果根据原始变量的数值计算相关系数，使用简捷公式计算相关系数可有效减少计算带来的误差。

2.相关系数的性质

相关系数r的取值范围为[-1，1]，即-1≤r≤1。r的取值越接近于1或-1，表明x与y直线相关程度越高；r越接近于0，表明x与y直线相关程度越低。r=1或r=-1，表明x与y之间完全线性相关，即x与y之间存在确定的函数关系；r=0，表示x与y之间不存在线性相关关系，但是不能排除两个变量之间存在曲线相关关系；r>0，表明x与y之间呈正直线相关关系；r<0，表明x与y之间呈负直线相关关系。

实践中，为了在判别相关关系的密切程度时有一个临界标准，可参考相关程度判别标准，如表7-3所示。

表7-3　相关程度判别标准

3.相关系数的计算(www.daowen.com)

【例7-1】某地区人均年纯收入（自变量）与其耐用消费品销售额（因变量）的资料如表7-4所示。试据此计算二者之间的相关系数，并说明二者之间相关关系的密切程度。

表7-4　相关系数计算表

将表7-4中的资料代入简捷公式，则

r=0.98，说明该地区人均年纯收入与耐用消费品销售额之间存在高度正相关关系。一般来讲，人们的年收入低，购买耐用消费品的支出就少；年收入高，在满足了基本生活支出后，购买耐用消费品的可能性就大。

4.相关系数的显著性检验

一般情况下，总体相关系数ρ是未知的，我们往往将样本的相关系数r作为ρ的估计值。但从同一总体中抽出不同样本来计算的r是不同的，因此样本相关系数r是一个随机变量。样本相关系数能否说明总体的相关程度呢？如果样本相关系数较高，则能否认为总体的相关系数也较高呢？在实际问题中，r对ρ的代表程度往往和样本容量有很大关系。对于不相关的两个变量，利用样本数据计算的r不一定等于零，有时会较高，这就会产生虚假相关现象。为判断r对ρ的代表性大小，需要对相关系数进行检验，即先假设ρ=ρ0，继而通过r提供的信息来检验ρ=ρ0的假设。如果ρ=ρ0通过检验，则说明r抽自ρ=ρ0的总体，r可以作为ρ的一个代表值；如果ρ=ρ0没有通过检验，则说明r不是抽自ρ=ρ0的总体，r不能作为ρ的一个代表值。下面只介绍在小样本的情况下检验ρ=0的假设问题。

检验ρ=0的假设实际上是判断样本相关系数是否抽自具有零相关的总体。在小样本（n<30）情况下，通常采用t检验方法检验，具体步骤如下：

第一步，建立假设。假设样本相关系数r是抽自具有零相关的总体，即

第二步，计算检验统计量。

第三步，确定显著性水平并得出结论。设显著性水平为α（通常取α值为0.05），根据自由度n-2，查t分布表得到检验统计量的临界值。若，则接受原假设H0，表明r在统计上是不显著的，即变量x与y之间的相关关系不显著；若，则拒绝原假设H0，表明r在统计上是显著的，即变量x与y之间的相关关系是显著的。

相关与回归分析（上）（教学视频）