实践中最常见的统计量主要有样本均值、样本比例和样本方差，给出这些常用的样本统计量的抽样分布，有助于更加便捷地进行统计推断。

1.样本均值的抽样分布

样本均值的抽样分布是指在重复选取容量为n的样本时，由样本均值的所有可能取值形成的相对频数分布。为更好地理解样本均值的抽样分布的概念，我们来看一个简单的例子。

【例6-1】设一个总体含有4个个体（元素），即N=4，取值分别为：x1=1，x2=2，x3=3，x4=4。我们先来看一下总体分布状况，如图6-1所示。

图6-1　总体分布

可以看出，总体分布为均匀分布，即每一个观察值xi的概率相等。这样，可以按下面的公式计算总体均值和方差，即

若从总体中采取重复抽样方法随机抽取容量为n=2的样本，则共有42=16个可能样本，具体如表6-1所示。

表6-1　可能的样本及其均值

续表

每个样本被抽中的概率相同，均为1/16。

样本均值的抽样分布如表6-2和图6-2所示。

表6-2　样本均值的抽样分布

图6-2　样本均值的抽样分布

由表6-2可以算出：

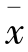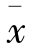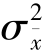通过计算可以发现，样本均值的均值μ¯x正好等于总体的均值，样本均值的方差正好等于总体方差σ2的1/n。这个结论不仅在本例中成立，而且具有普遍意义。统计学已经证明，关于作为随机变量的样本均值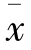抽样分布，有以下结论成立：

设总体共有N个元素，其均值为μ，方差为σ2，从中抽取容量为n的样本，样本均值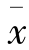的均值和方差分别记为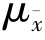和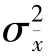，则无论是重复抽样还是不重复抽样，样本均值的数学期望始终等于总体均值，即

此外，样本均值的抽样方差与抽样方法有关。

1）在重复抽样条件下，样本均值的抽样方差为总体方差的1/n，即。

2）在不重复抽样条件下，样本均值的抽样方差则需要用修正系数加以修正，即(www.daowen.com)

对无限总体进行不重复抽样时，可以按重复抽样来处理，因为其修正系数趋近于1。对于有限总体来说，当N很大而n很小时，其修正系数也趋近于1，这时样本均值的方差也可以按来计算。

2.样本比例的抽样分布

样本比例是指总体（或样本）中具有某种属性的单位数与全部单位数之比，如一个班级中不同性别的人数与全班总人数之比，合格品（或不合格品）与全部产品总数之比等。在实际生活中，经常会用样本比例p去推断总体的比例P。

就一个具有N个元素的总体而言，具有不同属性的元素的个数分别为N0和N1，则总体比例可表示为

相应的样本比例可表示为

在重复抽取容量为n的样本时，由样本比例的所有可能取值形成的相对频数分布，称为样本比例的抽样分布。样本比例p的抽样分布是其所有可能取值的概率分布。当样本容量很大时，样本比例p的抽样分布可用正态分布近似表示。

同样，对于p的分布，也需要知道p的数学期望和方差。可以证明，p的数学期望E（p）等于总体的比例P，即E（p）=P。p的方差则与抽样方法有关。

设p的抽样方差为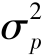，则

1）在重复抽样条件下，有

2）在不重复抽样条件下，用修正系数加以修正，有

与样本均值分布的方差一样，对无限总体进行不重复抽样时，可以按重复抽样来处理。此时，样本比例的方差仍可按计算；对有限总体，当N很大而抽样比时，其修正系数趋于1，这时样本比例的方差也可以按计算。

样本比例的抽样分布是一种理论上的概率分布，是推断总体比例P的基础。

3.样本方差的抽样分布

反复抽取样本容量相同的独立同分布样本，所得到的样本方差的概率分布称为样本方差的抽样分布。样本方差的抽样分布比较复杂，依据其变量分布的不同而不同。这里，仅就常用的变量服从正态分布时的样本方差的抽样分布进行讨论。

在X～N（μ，σ2）的同分布总体中，抽取样本容量为n的样本，其样本方差与总体方差的比值服从自由度为（n-1）的χ2分布，即

χ2分布是由阿贝（Abbe）于1863年首先提出，后来由海尔默特（Hermert）和卡·皮尔逊（K.Pearson）分别于1875年和1900年推导出来的。χ2分布仅在第一象限取值，所以χ2分布的取值永远为正数。χ2分布一般为右偏态的偏峰分布，具体偏倚形态取决于其自由度的数值，自由度的数值越小，偏倚的程度越大；并且随着自由度的数值增大，χ2分布的形态逐渐趋于对称，当n→∞时，χ2分布趋于正态分布，即正态分布是χ2分布的极限分布。下面对样本统计量的抽样分布形式进行概括，如图6-3所示。

图6-3　样本统计量的抽样分布形式

抽样分布（教学视频）