抽样分布是指样本统计量的概率分布。由于样本统计量是由n个随机变量构成的样本的函数，因此抽样分布属于随机变量函数的分布。例如在简单随机抽样时，总体有N个单位，从中按不考虑顺序、不重复抽样方式抽取n个单位进行调查，可抽取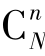个样本数目，可得到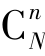个不尽相同的样本均值，经整理，将样本均值的全部可能取值及其出现的概率依次排列，就得到样本均值的概率分布，即样本均值的抽样分布。同理，可得到样本成数的抽样分布、样本方差的抽样分布等。

为了更好地掌握抽样分布的原理，需要先了解三种不同性质的分布，即总体分布、样本分布和抽样分布，掌握三者之间的区别与联系。

1.总体分布

总体分布是指总体中各元素的观测值所形成的相对频数分布。假如可对总体中所有观测值做一次全面普查，则可通过直方图观测该总体的分布状况。但在现实中，总体的分布往往是不知道的，通常是根据经验大致了解总体的分布类型，或者假定它服从某种分布，然后再用样本分布推断总体分布。例如，先假定某种小包装茶叶的质量服从正态分布，然后在全部小包装茶叶中按随机原则抽取部分来测定，最后用部分小包装茶叶的样本分布推断总体分布。

2.样本分布

样本分布是指从总体中抽取一个容量为n的样本后，由这n个观测值形成的相对频数分布。由于样本是从总体中抽取的，其中包含着总体的一些信息和特征，因此样本分布也称经验分布。一般地，当样本量较大或逐渐增大时，样本分布也逐渐接近于总体分布；但当样本量较小或受随机因素影响时，样本分布也可能与总体分布不一致，甚至会有较大差异。值得注意的是，样本分布是指一个样本中各观测值的分布，它与抽样分布是不同的。

3.抽样分布

抽样分布是指样本统计量的概率分布。理论上，抽样分布是指从容量为N的总体中抽取容量为n的样本时，所有样本可能数目的统计量取值所形成的相对频数分布。由于现实中不可能将所有的样本都抽出来，因此统计量的抽样分布实际上是一种理论分布。在通常情况下，总体的参数是根据样本统计量推断的，如用样本均值去推断总体均值，用样本比例去推断总体比例、用样本标准差去推断总体标准差等，那么进行这种推断的理论依据就是统计量的抽样分布。可以说，抽样分布是研究样本分布与总体分布之间关系的桥梁。

抽样分布是指样本统计量的概率分布。由于样本统计量是由n个随机变量构成的样本的函数，因此抽样分布属于随机变量函数的分布。例如在简单随机抽样时，总体有N个单位，从中按不考虑顺序、不重复抽样方式抽取n个单位进行调查，可抽取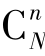个样本数目，可得到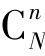个不尽相同的样本均值，经整理，将样本均值的全部可能取值及其出现的概率依次排列，就得到样本均值的概率分布，即样本均值的抽样分布。同理，可得到样本成数的抽样分布、样本方差的抽样分布等。(www.daowen.com)

为了更好地掌握抽样分布的原理，需要先了解三种不同性质的分布，即总体分布、样本分布和抽样分布，掌握三者之间的区别与联系。

1.总体分布

总体分布是指总体中各元素的观测值所形成的相对频数分布。假如可对总体中所有观测值做一次全面普查，则可通过直方图观测该总体的分布状况。但在现实中，总体的分布往往是不知道的，通常是根据经验大致了解总体的分布类型，或者假定它服从某种分布，然后再用样本分布推断总体分布。例如，先假定某种小包装茶叶的质量服从正态分布，然后在全部小包装茶叶中按随机原则抽取部分来测定，最后用部分小包装茶叶的样本分布推断总体分布。

2.样本分布

样本分布是指从总体中抽取一个容量为n的样本后，由这n个观测值形成的相对频数分布。由于样本是从总体中抽取的，其中包含着总体的一些信息和特征，因此样本分布也称经验分布。一般地，当样本量较大或逐渐增大时，样本分布也逐渐接近于总体分布；但当样本量较小或受随机因素影响时，样本分布也可能与总体分布不一致，甚至会有较大差异。值得注意的是，样本分布是指一个样本中各观测值的分布，它与抽样分布是不同的。

3.抽样分布

抽样分布是指样本统计量的概率分布。理论上，抽样分布是指从容量为N的总体中抽取容量为n的样本时，所有样本可能数目的统计量取值所形成的相对频数分布。由于现实中不可能将所有的样本都抽出来，因此统计量的抽样分布实际上是一种理论分布。在通常情况下，总体的参数是根据样本统计量推断的，如用样本均值去推断总体均值，用样本比例去推断总体比例、用样本标准差去推断总体标准差等，那么进行这种推断的理论依据就是统计量的抽样分布。可以说，抽样分布是研究样本分布与总体分布之间关系的桥梁。