1.全及总体和样本总体

（1）全及总体

全及总体简称总体，是所研究对象的全体，它是由具有某种共同性质或特征的许多单位组成的集合体。总体明确了抽样调查的范围。例如，从某校1 000名学生中，随机抽取100名学生进行身体健康状况的调查，这1 000名学生即全及总体。通常用英文大写字母N表示全及总体中的单位数，如上例中取N=1 000人。对于某一具体问题来说，总体是唯一的、确定的，但是，总体中的某些数量特征是未知的。正是由于总体存在未知的数量特征，因此才有必要进行抽样调查。

总体按所研究单位的性质，可以分为变量总体和属性总体两类。对于一个总体来说，若所研究单位的标志属于品质标志，则该总体为属性总体；若所研究单位的标志属于数量标志，则该总体为变量总体。对于变量总体又可按其所包含的单位数以及相应变量的多少分为无限总体和有限总体。

（2）样本总体

样本总体简称样本，是由按随机性原则从全及总体中抽取的部分单位组成的集合体。样本的单位数是有限的，相对来说，它的数目比较小，一般以小写英文字母n表示。例如，某城市从全部住户中随机抽取1 000户进行调查，则被抽中的1 000户构成样本总体（即样本），样本单位数n=1 000户。一般地，作为调查对象的总体是确定的，而且是唯一的。但作为观察对象的样本就不是这样，从一个总体可以抽取很多个样本，每次可能抽到哪个样本不是确定的，也不是唯一的，而是可变的。

2.总体参数和样本统计量

（1）总体参数

总体参数又称总体指标或全及指标，它是根据总体中各单位的变量值或属性特征计算的、用以反映总体数量特征的综合指标。常用的总体参数有总体平均数、总体成数、总体数量标志标准差（σ）及总体方差（σ2）、总体是非标志标准差（σP）等，它们是反映总体分布特征的重要指标。由于总体是唯一确定的，故根据总体计算的指标也是唯一确定的，但它是未知数，可以通过样本指标来推断。

1）总体平均数。总体平均数又称全及平均数，是代表总体单位数量标志一般水平的指标。它表明变量变动的集中趋势，通常用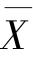 表示，即

式中，X表示总体各单位的标志值；F表示总体各组次数。

2）总体成数。总体成数又称全及成数，对于属性总体，它是指当总体可以按交替标志划分为两个组成部分时，其中具有某一相同标志表现的总体单位数在总体中所占的比例，通常用P表示；不具有某一标志表现的总体单位数在总体中所占的比例，用Q表示。若以N1代表具有某种相同标志表现的单位数，以N0代表不具有某种相同标志表现的单位数，且N=N1+N0，则总体成数为

其中，成数是是非标志的平均数。所谓是非标志，就是指只能取两种标志表现的标志。假定具有某种相同标志表现的变量值记为1，不具备该种标志表现的变量值记为0，那么成数P可以看作这两个变量的加权算术平均数，即P是是非标志的平均数。

3）总体数量标志标准差及总体方差。总体数量标志标准差是指总体中根据各单位标志值计算的标准差，记作σ。

该标准差的平方叫作总体方差，记作σ2。

1）总体平均数。总体平均数又称全及平均数，是代表总体单位数量标志一般水平的指标。它表明变量变动的集中趋势，通常用 表示，即

式中，X表示总体各单位的标志值；F表示总体各组次数。

2）总体成数。总体成数又称全及成数，对于属性总体，它是指当总体可以按交替标志划分为两个组成部分时，其中具有某一相同标志表现的总体单位数在总体中所占的比例，通常用P表示；不具有某一标志表现的总体单位数在总体中所占的比例，用Q表示。若以N1代表具有某种相同标志表现的单位数，以N0代表不具有某种相同标志表现的单位数，且N=N1+N0，则总体成数为

其中，成数是是非标志的平均数。所谓是非标志，就是指只能取两种标志表现的标志。假定具有某种相同标志表现的变量值记为1，不具备该种标志表现的变量值记为0，那么成数P可以看作这两个变量的加权算术平均数，即P是是非标志的平均数。

3）总体数量标志标准差及总体方差。总体数量标志标准差是指总体中根据各单位标志值计算的标准差，记作σ。

该标准差的平方叫作总体方差，记作σ2。

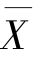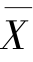1）总体平均数。总体平均数又称全及平均数，是代表总体单位数量标志一般水平的指标。它表明变量变动的集中趋势，通常用 表示，即

式中，X表示总体各单位的标志值；F表示总体各组次数。

2）总体成数。总体成数又称全及成数，对于属性总体，它是指当总体可以按交替标志划分为两个组成部分时，其中具有某一相同标志表现的总体单位数在总体中所占的比例，通常用P表示；不具有某一标志表现的总体单位数在总体中所占的比例，用Q表示。若以N1代表具有某种相同标志表现的单位数，以N0代表不具有某种相同标志表现的单位数，且N=N1+N0，则总体成数为

其中，成数是是非标志的平均数。所谓是非标志，就是指只能取两种标志表现的标志。假定具有某种相同标志表现的变量值记为1，不具备该种标志表现的变量值记为0，那么成数P可以看作这两个变量的加权算术平均数，即P是是非标志的平均数。

3）总体数量标志标准差及总体方差。总体数量标志标准差是指总体中根据各单位标志值计算的标准差，记作σ。

该标准差的平方叫作总体方差，记作σ2。

4）总体是非标志标准差。总体是非标志标准差是指全及总体中根据是非标志计算的标准差。总体是非标志标准差为，具体推导为

（2）样本统计量

4）总体是非标志标准差。总体是非标志标准差是指全及总体中根据是非标志计算的标准差。总体是非标志标准差为，具体推导为

（2）样本统计量

4）总体是非标志标准差。总体是非标志标准差是指全及总体中根据是非标志计算的标准差。总体是非标志标准差为，具体推导为

（2）样本统计量

样本统计量即样本指标，是由样本中各单位的变量值或属性特征计算的反映样本数量特征的综合指标。由于从一个总体中可以抽取多个样本，样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。与总体指标相对应，样本统计量有样本平均数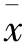（）、样本成数（p）、样本数量标志标准差（s）及方差（s2）、样本是非标志标准差（sp）及方差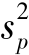（）等。为了与总体指标区别，样本指标用小写字母表示。1）样本平均数。样本平均数是抽样总体各单位标志值的平均数，用¯x表示。

式中，x表示样本各单位标志值；f表示样本各组次数。

2）样本成数。设样本的n个单位中有n1个单位具有某种标志表现，n0个不具有某种标志表现，且n=n1+n0，则样本成数为

3）样本数量标志的标准差及样本方差。样本数量标志的标准差是说明样本总体之间标志值变异程度的指标，记作s；其平方称为样本方差，记作s2。

4）样本是非标志标准差。样本是非标志标准差是指样本中根据是非标志计算的标准差，样本是非标志标准差的计算公式为

由于从一个总体中可以抽取多个样本，而样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。

3.样本容量和样本个数

（1）样本容量

样本容量和样本个数是两个互相联系但又完全不同的概念。样本容量是指一个样本所包含的单位数。一个样本应该包含多少单位最合适，是抽样设计必须认真考虑的问题，必须结合调查任务的要求以及总体标志值的变异情况来考虑。样本容量的大小不但关系到抽样调查的效果，而且关系到抽样方法的应用。

样本按照样本容量的多少分为大样本和小样本。当n≥30时，称为大样本；当n<30时，称为小样本。通常，社会经济现象的抽样调查多取大样本，自然试验观察则多取小样本。

（2）样本个数

样本个数又称样本可能数目，是指从一个总体上可能抽取的样本个数。一个总体可能抽取多少样本，和样本容量以及抽样方法等因素有关，是一个比较复杂的问题。一个总体有多少样本，样本统计量就有多少种取值，从而形成统计量的分布。统计量的分布是抽样调查的基础。虽然在实践上只抽取个别或少数样本，但要判断所取样本的可能性就必须联系全部可能抽取样本数目所形成的分布。

4.重复抽样和不重复抽样

根据取样方式不同，抽样方法分为重复抽样和不重复抽样。

（1）重复抽样

重复抽样也叫重置抽样，其操作方法是：从总体N个单位中随机抽取一个容量为n的样本，每次从总体中抽取一个单位，把它看作一次试验；每次抽出一个单位并登记后，又重新放回总体中，参加下一次抽选，连续进行n次试验就构成一个样本。重复抽样的特点是共由n次相互独立的试验构成，每次试验是在相同的条件下进行的，即在整个抽取样本的过程中，总体单位数始终保持不变，每个单位的中选机会在各次是相等的。

例如，总体有A、B、C、D四个单位，要从中随机重复抽取两个单位构成一个样本。先从四个单位中抽取一个单位，结果登记后放回，然后从相同的四个单位中抽取第二个单位，就构成了一个样本，全部可能抽取的样本数目为42种，其具体样本组合为：AA、AB、AC、AD、BA、BB、BC、BD、CA、CB、CC、CD、DA、DB、DC、DD，共16个样本。

一般地，从总体N个单位中随机重复抽取n个单位构成一个样本，则共可抽取Nn个样本组合。

（2）不重复抽样(www.daowen.com)

不重复抽样也叫不重置抽样，其抽样的操作方法是：从总体N个单位中抽取一个容量为n的样本，每次从总体中抽取一个单位（每次抽取的样本不再放回）。连续进行n次抽取，就构成了一个样本。不重复抽样的特点是样本是由n次连续抽取结果构成，实质上等于一次同时从总体中抽取n个样本单位，所以连续n次抽选的结果不是相互独立的；第一次抽取的结果会影响下一次的抽取，每抽一次，总体单位数就减少一个；每个单位的中选机会在各次是不相等的。

例如，总体有A、B、C、D四个单位，用随机不重复的方法从中抽取两个单位构成一个样本，则全部可能的样本数目为4×3=12（种）。其具体的样本组合为：AB、AC、AD、BA、BC、BD、CA、CB、CD、DA、DB、DC，共12个样本。

一般地，从总体N个单位中随机不重复抽取n个单位构成一个样本，则共有样本组合为

由此可见，在相同的样本容量要求下，不重复抽样的样本个数总是比重复抽样的样本个数少。

样本统计量即样本指标，是由样本中各单位的变量值或属性特征计算的反映样本数量特征的综合指标。由于从一个总体中可以抽取多个样本，样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。与总体指标相对应，样本统计量有样本平均数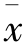（）、样本成数（p）、样本数量标志标准差（s）及方差（s2）、样本是非标志标准差（sp）及方差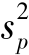（）等。为了与总体指标区别，样本指标用小写字母表示。1）样本平均数。样本平均数是抽样总体各单位标志值的平均数，用¯x表示。

式中，x表示样本各单位标志值；f表示样本各组次数。

2）样本成数。设样本的n个单位中有n1个单位具有某种标志表现，n0个不具有某种标志表现，且n=n1+n0，则样本成数为

3）样本数量标志的标准差及样本方差。样本数量标志的标准差是说明样本总体之间标志值变异程度的指标，记作s；其平方称为样本方差，记作s2。

4）样本是非标志标准差。样本是非标志标准差是指样本中根据是非标志计算的标准差，样本是非标志标准差的计算公式为

由于从一个总体中可以抽取多个样本，而样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。

3.样本容量和样本个数

（1）样本容量

样本容量和样本个数是两个互相联系但又完全不同的概念。样本容量是指一个样本所包含的单位数。一个样本应该包含多少单位最合适，是抽样设计必须认真考虑的问题，必须结合调查任务的要求以及总体标志值的变异情况来考虑。样本容量的大小不但关系到抽样调查的效果，而且关系到抽样方法的应用。

样本按照样本容量的多少分为大样本和小样本。当n≥30时，称为大样本；当n<30时，称为小样本。通常，社会经济现象的抽样调查多取大样本，自然试验观察则多取小样本。

（2）样本个数

样本个数又称样本可能数目，是指从一个总体上可能抽取的样本个数。一个总体可能抽取多少样本，和样本容量以及抽样方法等因素有关，是一个比较复杂的问题。一个总体有多少样本，样本统计量就有多少种取值，从而形成统计量的分布。统计量的分布是抽样调查的基础。虽然在实践上只抽取个别或少数样本，但要判断所取样本的可能性就必须联系全部可能抽取样本数目所形成的分布。

4.重复抽样和不重复抽样

根据取样方式不同，抽样方法分为重复抽样和不重复抽样。

（1）重复抽样

重复抽样也叫重置抽样，其操作方法是：从总体N个单位中随机抽取一个容量为n的样本，每次从总体中抽取一个单位，把它看作一次试验；每次抽出一个单位并登记后，又重新放回总体中，参加下一次抽选，连续进行n次试验就构成一个样本。重复抽样的特点是共由n次相互独立的试验构成，每次试验是在相同的条件下进行的，即在整个抽取样本的过程中，总体单位数始终保持不变，每个单位的中选机会在各次是相等的。

例如，总体有A、B、C、D四个单位，要从中随机重复抽取两个单位构成一个样本。先从四个单位中抽取一个单位，结果登记后放回，然后从相同的四个单位中抽取第二个单位，就构成了一个样本，全部可能抽取的样本数目为42种，其具体样本组合为：AA、AB、AC、AD、BA、BB、BC、BD、CA、CB、CC、CD、DA、DB、DC、DD，共16个样本。

一般地，从总体N个单位中随机重复抽取n个单位构成一个样本，则共可抽取Nn个样本组合。

（2）不重复抽样

不重复抽样也叫不重置抽样，其抽样的操作方法是：从总体N个单位中抽取一个容量为n的样本，每次从总体中抽取一个单位（每次抽取的样本不再放回）。连续进行n次抽取，就构成了一个样本。不重复抽样的特点是样本是由n次连续抽取结果构成，实质上等于一次同时从总体中抽取n个样本单位，所以连续n次抽选的结果不是相互独立的；第一次抽取的结果会影响下一次的抽取，每抽一次，总体单位数就减少一个；每个单位的中选机会在各次是不相等的。

例如，总体有A、B、C、D四个单位，用随机不重复的方法从中抽取两个单位构成一个样本，则全部可能的样本数目为4×3=12（种）。其具体的样本组合为：AB、AC、AD、BA、BC、BD、CA、CB、CD、DA、DB、DC，共12个样本。

一般地，从总体N个单位中随机不重复抽取n个单位构成一个样本，则共有样本组合为

由此可见，在相同的样本容量要求下，不重复抽样的样本个数总是比重复抽样的样本个数少。

样本统计量即样本指标，是由样本中各单位的变量值或属性特征计算的反映样本数量特征的综合指标。由于从一个总体中可以抽取多个样本，样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。与总体指标相对应，样本统计量有样本平均数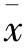（）、样本成数（p）、样本数量标志标准差（s）及方差（s2）、样本是非标志标准差（sp）及方差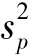（）等。为了与总体指标区别，样本指标用小写字母表示。1）样本平均数。样本平均数是抽样总体各单位标志值的平均数，用¯x表示。

式中，x表示样本各单位标志值；f表示样本各组次数。

2）样本成数。设样本的n个单位中有n1个单位具有某种标志表现，n0个不具有某种标志表现，且n=n1+n0，则样本成数为

3）样本数量标志的标准差及样本方差。样本数量标志的标准差是说明样本总体之间标志值变异程度的指标，记作s；其平方称为样本方差，记作s2。

4）样本是非标志标准差。样本是非标志标准差是指样本中根据是非标志计算的标准差，样本是非标志标准差的计算公式为

由于从一个总体中可以抽取多个样本，而样本不同，样本指标的数值也不同，因此样本指标不是唯一确定的，是个随机变量。

3.样本容量和样本个数

（1）样本容量

样本容量和样本个数是两个互相联系但又完全不同的概念。样本容量是指一个样本所包含的单位数。一个样本应该包含多少单位最合适，是抽样设计必须认真考虑的问题，必须结合调查任务的要求以及总体标志值的变异情况来考虑。样本容量的大小不但关系到抽样调查的效果，而且关系到抽样方法的应用。

样本按照样本容量的多少分为大样本和小样本。当n≥30时，称为大样本；当n<30时，称为小样本。通常，社会经济现象的抽样调查多取大样本，自然试验观察则多取小样本。

（2）样本个数

样本个数又称样本可能数目，是指从一个总体上可能抽取的样本个数。一个总体可能抽取多少样本，和样本容量以及抽样方法等因素有关，是一个比较复杂的问题。一个总体有多少样本，样本统计量就有多少种取值，从而形成统计量的分布。统计量的分布是抽样调查的基础。虽然在实践上只抽取个别或少数样本，但要判断所取样本的可能性就必须联系全部可能抽取样本数目所形成的分布。

4.重复抽样和不重复抽样

根据取样方式不同，抽样方法分为重复抽样和不重复抽样。

（1）重复抽样

重复抽样也叫重置抽样，其操作方法是：从总体N个单位中随机抽取一个容量为n的样本，每次从总体中抽取一个单位，把它看作一次试验；每次抽出一个单位并登记后，又重新放回总体中，参加下一次抽选，连续进行n次试验就构成一个样本。重复抽样的特点是共由n次相互独立的试验构成，每次试验是在相同的条件下进行的，即在整个抽取样本的过程中，总体单位数始终保持不变，每个单位的中选机会在各次是相等的。

例如，总体有A、B、C、D四个单位，要从中随机重复抽取两个单位构成一个样本。先从四个单位中抽取一个单位，结果登记后放回，然后从相同的四个单位中抽取第二个单位，就构成了一个样本，全部可能抽取的样本数目为42种，其具体样本组合为：AA、AB、AC、AD、BA、BB、BC、BD、CA、CB、CC、CD、DA、DB、DC、DD，共16个样本。

一般地，从总体N个单位中随机重复抽取n个单位构成一个样本，则共可抽取Nn个样本组合。

（2）不重复抽样

不重复抽样也叫不重置抽样，其抽样的操作方法是：从总体N个单位中抽取一个容量为n的样本，每次从总体中抽取一个单位（每次抽取的样本不再放回）。连续进行n次抽取，就构成了一个样本。不重复抽样的特点是样本是由n次连续抽取结果构成，实质上等于一次同时从总体中抽取n个样本单位，所以连续n次抽选的结果不是相互独立的；第一次抽取的结果会影响下一次的抽取，每抽一次，总体单位数就减少一个；每个单位的中选机会在各次是不相等的。

例如，总体有A、B、C、D四个单位，用随机不重复的方法从中抽取两个单位构成一个样本，则全部可能的样本数目为4×3=12（种）。其具体的样本组合为：AB、AC、AD、BA、BC、BD、CA、CB、CD、DA、DB、DC，共12个样本。

一般地，从总体N个单位中随机不重复抽取n个单位构成一个样本，则共有样本组合为

由此可见，在相同的样本容量要求下，不重复抽样的样本个数总是比重复抽样的样本个数少。