指数体系的因素分析就是利用指数体系，从绝对数和相对数两个方面分析现象的总变动中受各影响因素变动的影响方向和影响程度。相对数分析就是根据指数体系，从统计指数计算结果本身指出现象总体总量指标或平均指标的变动受各个影响因素的作用程度和结果。绝对数分析就是通过指数体系中各个指数分子与分母之差，分析现象总变动差额与各影响因素变动差额之间的因果关系。

1.因素分析的步骤

因素分析法建立在现象之间的经济关系基础上，依据指数体系从相对数和绝对数两方面进行分析。具体分析步骤为：

第一步，建立指数体系，即总变动指数等于各影响因素指数的连乘积。

第二步，计算被分析统计指标的总变动。

第三步，计算各影响因素变动的影响程度和绝对值。

第四步，影响因素的综合分析，总变动程度等于各因素变动影响程度的连乘积；总变动绝对值等于各因素变动的绝对值之和。

2.总量指标变动的因素分析

总量指标变动的因素分析按照影响因素的多少，分为两因素分析和多因素分析。

（1）总量指标的两因素分析

【例5-6】根据资料分析总成本变动中产量和单位成本变动的影响程度，其资料如表5-7所示。

表5-7　某企业产量和单位成本统计

1）建立指数体系：总成本指数=产量指数×单位成本指数。

绝对数分析公式：

2）总成本的总变动分析。

计算结果表明，报告期总成本相比基期总成本增加了13.10％，绝对额增加了110元。

3）各因素变动对总成本影响相对程度及影响绝对额分析。

①产量变动的影响方向及影响程度分析，包括

计算结果表明，三种产品的报告期产量相比基期产量平均增加了7.14％，由此增加的总成本是60元。

②单位成本的影响方向和影响程度分析，包括

计算结果表明，三种产品报告期单位成本相比基期单位成本平均增加了5.56％，由此增加的总成本是50元。

4）综合分析，包括

即该企业的总成本在报告期增加了13.10％，总成本绝对值增加了110元。其中，产量增加了7.14％，使总成本绝对值增加了60元；单位成本增加了5.56％，使总成本绝对值增加了50元。

在指数体系的两因素分析中，建立指数体系是非常重要的。指数体系的建立要遵循一定原则：一是总变动的两个影响因素指数必须一个是数量指标指数，另一个是质量指标指数；二是两个影响因素指数的排列顺序，一般是先数量指标指数，后质量指标指数；三是两个影响因素指数不能同时是拉氏指数或同时是派氏指数，必须一个是拉氏指数，另一个是派氏指数，否则指数体系关系就不存在。

一般而言，应遵循综合指数的编制原则来建立指数体系，即数量指标指数是拉氏指数，同度量因素固定在基期；质量指标指数是派氏指数，同度量因素固定在报告期。

（2）总量指标的多因素分析

在实际分析中，有些现象受三个或三个以上因素的影响，例如：

利税总额=销售量×销售价格×利税率

工业产品原材料支出额=产品产量×单位产品原材料消耗量×原材料价格

当影响因素在三个或三个以上时，应用指数体系进行因素分析，其被称为多因素分析。

由于多因素分析的影响因素较多，编制过程比较复杂，因此编制时应注意以下问题：

1）分析、研究某个因素数量变化时，应先把其他因素固定下来。

2）合理安排多个影响因素的排列顺序。对各影响因素排序一般是数量指标在前、质量指标在后，外延因素在前、内涵因素在后，基础因素在前、派生因素在后。任何两个相邻因素的乘积都应该有实际经济意义。

3）分析某因素的变化时，其余因素均作为同度量因素固定。一般情况下，可按照综合指数的编制原则固定。具体固定方法为：当分析第一个因素的变动影响时，把其他所有因素作为同度量因素固定在基期；当分析第二个因素的影响时，则把已分析过的因素固定在报告期，没有分析过的因素固定在基期；以此类推，确定同度量因素的固定时期。

【例5-7】对某企业销售利润总额指数进行多因素分析，其销售统计数据如表5-8所示。

表5-8　某商业企业商品销售资料

由于销售利润总额=销售量×销售价格×销售利润率，故销售利润总额指数=销售量指数×销售价格指数×利润率指数。具体计算步骤如下：

（1）建立指数体系

（2）销售利润总额的总变动分析

即报告期销售利润总额相比基期销售利润总额增加了48.90％。

（3）各影响因素的变动程度和对销售利润总额的影响

1）销售量对销售利润额的影响。

即报告期销售量相比基期销售量平均增加了12.59％，从而使销售利润绝对额增加了

2）销售价格对销售利润总额的影响。

即报告期销售价格相比基期销售价格平均增长了7.22％，从而使销售利润绝对额增加了

3）销售利润率对利润额的影响。

报告期的销售利润率相比基期的销售利润率，平均增加了23.34％，从而增加的销售利润绝对额为(www.daowen.com)

（4）影响因素的综合分析

相对数分析：148.90％=112.59％×107.22％×123.34％

绝对数分析：4 000（元）=1 030（元）+665（元）+2 305（元）

计算结果表明，报告期的销售量平均增加了12.59％，销售价格平均增加了7.22％，销售利润率增加了23.34％。这三方面因素的共同影响，使该企业销售利润总额增加了48.90％，销售利润绝对额增加了4 000元。这是销售量增加和销售价格上涨分别使销售利润绝对额增加1 030元和665元，以及由于销售利润率提高而增加了2 305元的综合影响结果。

3.平均指标对比指数及其因素分析

在实际运用中，常常需要对平均指标的变动进行对比分析。在分组条件下，总平均指标的变动受两个因素的影响：一是各组的变量水平（常用x表示）；二是总体的结构（常用 表示），即各组单位数占总体单位数的比例。

在平均数变动的因素分析中，通常将各组单位数占总体单位数的比例看成数量指标，而将各组的变量平均水平看成质量指标。运用指数体系因素分析法，可以分析各因素变动对总平均指标变动的影响方向和程度。总平均指标变动的因素分析，需要区分三种平均指标指数，即可变构成指数、固定构成指数和结构变动影响指数。三者间的关系为

可变构成指数=固定构成指数×结构变动影响指数

（1）可变构成指数

可变构成指数也叫平均指标对比指数，是指在分组条件下综合反映水平和结构两个因素共同变化所引起的总平均水平的变动指数。其计算公式为

式中，和分别表示某变量在报告期和基期的平均值。

可变构成指数的分子与分母之差，表明报告期总平均指标与基期总平均指标相差的绝对额，即

（2）固定构成指数

固定构成指数是指在分组条件下，将结构因素固定在报告期，借以反映各水平变动对总

平均指标的影响指数。其计算公式为

式中，表示以基期变量x0与报告期结构为权重因子而计算的假定平均值。

固定构成指数的分子与分母之差，表明各组水平因素变动对总平均指标变动影响的绝对额，即

（3）结构变动影响指数

它是指在分组条件下，将各组水平固定在基期，以单纯反映结构因素变动对总平均指标的影响指数。其计算公式为

结构变动影响指数的分子与分母之差，表明各组变量x0固定时，各组结构因素变动对总平均指标的绝对影响，即

三者构造的指数体系为：

1）相对数形式：可变构成指数=固定构成指数×结构变动影响指数，即

可简记为

2）绝对数形式：增加的总平均数=由于水平变化增加的平均数+由于结构变化增加的平均数，即

可简记为

【例5-8】对某企业工人总平均工资的变化情况进行因素分析，该公司下属三个企业的工资资料如表5-9所示。

表5-9　某公司企业职工人数、平均工资资料表

用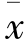、f分别表示平均工资和人数，则有

（1）总平均工资的变动

总平均工资的变动

计算结果表明，报告期总平均工资比基期总平均工资上涨了6.86％，由此增加的总平均工资为

其中：

1）受各组工人平均工资水平变动的影响：

计算结果表明，各企业职工工资水平上涨，使总平均工资提高了9.01％，由此增加的总平均工资为

2）受各组工人人数比例变化的影响：

计算结果表明，各企业职工人数的比例变动使总平均工资降低了1.97％，由此减少的总平均工资为

（2）综合分析

相对数分析：106.86％=109.01％×98.03％

绝对数分析：60.69元=78.12元+（-17.43）元

即该公司职工报告期的工资水平相比基期平均提高了6.86％，平均每人增加了60.69元。其中，各企业职工工资上涨使总平均工资提高了9.01％，即每位职工工资绝对数增加了78.12元；工资水平高的丙企业职工人数的比例下降使总平均工资下降了1.97％，即每位职工工资绝对数减少了17.43元。二者共同作用的结果，最终使总平均工资增加了6.86％，平均每人增加了60.69元。

此外，如果想要了解总平均工资变化对工资总额变化的影响，则可以将上述分析结果直接乘以报告期的职工人数∑f1求得。本例中，由于总平均工资上涨，所增加的工资总额为

其中，受各企业职工平均工资水平上涨而增加的总额为

受各企业职工人数比例变化而减少的总额为

指数体系与因素分析（教学视频）

知识与能力训练

[1]资料来源：《中华人民共和国2016年国民经济和社会发展统计公报》。