1.确定指数化因素

指数化因素是指通过编制综合指数来反映其变化程度的那个因素，如物量指数的销售量。与指数化因素相对应的另一个概念是同度量因素，同度量因素是将原来不能同度量的指数化因素转变为能度量的那个媒介因素。例如，在编制销售量总指数时，需要引入销售价格，用不同商品销售量乘以各自对应的销售价格，把不能同度量的销售量转化为可以同度量的销售额后，就可以直接相加了，这里销售价格就是同度量因素。

通常，将指数化因素是数量指标的综合指数称为数量指标指数，指数化因素是质量指标的综合指数称为质量指标指数。

2.确定同度量因素

编制综合指数时，首先必须解决不同事物数量的不同度量问题，设法找到一个媒介因素（即同度量因素），以解决复杂现象总体的指数化指标不能直接加总的问题。同度量因素有两个作用，如编制商品零售价格总指数时，需要以商品销售量为同度量因素，由于销售量高的商品其销售额也高，相应地对总指数的影响就大，因此同度量因素也称为权数。而在编制销售量指数时，销售量是指数化因素，单位商品销售价格是同度量因素。

3.确定同度量因素的时期

确定同度量因素的时期应从实际情况出发，根据编制综合指数的具体目的、任务和研究对象的经济内容来确定。

同度量因素的时期选择不同，有不同的综合指数计算公式，国际上通用的是拉氏指数和派氏指数。

（1）拉氏指数

拉氏指数是德国统计学家拉斯佩尔于1864年提出的一种综合指数计算方法。利用它计算综合指数时，将同度量因素固定在基期，如计算价格综合指数时，以基期的数量指标（如产量或销售量）作为同度量因素；在计算数量指标指数时，也以基期的质量指标（如价格）作为同度量因素。其计算公式为

式中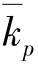，表示质量指标指数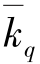；表示数量指标指数；q表示数量指标；p表示质量指标；1表示报告期；0表示基期。

拉氏指数将同度量因素固定在基期水平，故又称为基期加权综合指数。拉氏指数可以消除权数变动对指数的影响，从而使不同时期的综合指数具有可比性。

（2）派氏指数

派氏指数是1874年德国另一位经济学家哈曼·派许提出的一种计算综合指数的方法。利用它计算综合指数时，将同度量因素固定在报告期。如计算综合价格指数时，以报告期的数量指标（如产量或销售量）作为同度量因素。其计算公式为

因派氏指数将同度量因素固定在报告期水平，故又称为报告期加权综合指数。派氏指数不能消除权数变动对指数的影响，因而不同时期的综合指数缺乏可比性。但派氏指数能反映质量指标（如商品价格）和数量指标（如销售量）的同时变动，具有较明显的经济意义。

在实际统计工作中，常用拉氏公式来计算数量指标（如产量和销售量）指数；用派氏公式来计算质量指标（如价格、成本）指数。(www.daowen.com)

我国综合指数编制理论和实践遵循的一般原则是：数量指标指数用拉氏公式，即以基期质量指标作为同度量因素；质量指标指数用派氏公式，即以报告期数量指标作为同度量因素。

式中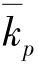，表示质量指标指数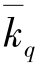；表示数量指标指数；q表示数量指标；p表示质量指标；1表示报告期；0表示基期。

拉氏指数将同度量因素固定在基期水平，故又称为基期加权综合指数。拉氏指数可以消除权数变动对指数的影响，从而使不同时期的综合指数具有可比性。

（2）派氏指数

派氏指数是1874年德国另一位经济学家哈曼·派许提出的一种计算综合指数的方法。利用它计算综合指数时，将同度量因素固定在报告期。如计算综合价格指数时，以报告期的数量指标（如产量或销售量）作为同度量因素。其计算公式为

因派氏指数将同度量因素固定在报告期水平，故又称为报告期加权综合指数。派氏指数不能消除权数变动对指数的影响，因而不同时期的综合指数缺乏可比性。但派氏指数能反映质量指标（如商品价格）和数量指标（如销售量）的同时变动，具有较明显的经济意义。

在实际统计工作中，常用拉氏公式来计算数量指标（如产量和销售量）指数；用派氏公式来计算质量指标（如价格、成本）指数。

我国综合指数编制理论和实践遵循的一般原则是：数量指标指数用拉氏公式，即以基期质量指标作为同度量因素；质量指标指数用派氏公式，即以报告期数量指标作为同度量因素。

式中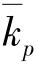，表示质量指标指数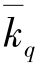；表示数量指标指数；q表示数量指标；p表示质量指标；1表示报告期；0表示基期。

拉氏指数将同度量因素固定在基期水平，故又称为基期加权综合指数。拉氏指数可以消除权数变动对指数的影响，从而使不同时期的综合指数具有可比性。

（2）派氏指数

派氏指数是1874年德国另一位经济学家哈曼·派许提出的一种计算综合指数的方法。利用它计算综合指数时，将同度量因素固定在报告期。如计算综合价格指数时，以报告期的数量指标（如产量或销售量）作为同度量因素。其计算公式为

因派氏指数将同度量因素固定在报告期水平，故又称为报告期加权综合指数。派氏指数不能消除权数变动对指数的影响，因而不同时期的综合指数缺乏可比性。但派氏指数能反映质量指标（如商品价格）和数量指标（如销售量）的同时变动，具有较明显的经济意义。

在实际统计工作中，常用拉氏公式来计算数量指标（如产量和销售量）指数；用派氏公式来计算质量指标（如价格、成本）指数。

我国综合指数编制理论和实践遵循的一般原则是：数量指标指数用拉氏公式，即以基期质量指标作为同度量因素；质量指标指数用派氏公式，即以报告期数量指标作为同度量因素。