平均数按计算方法、表现形式和作用的不同，可分为数值平均数和位置平均数两大类。

1.数值平均数

数值平均数是根据数据分布的全部标志值（或称变量值）计算的平均数，也称均值，是反映数据分布集中趋势的重要指标。它又包括算术平均数、调和平均数和几何平均数。

（1）算术平均数

算术平均数是分析社会经济现象一般水平的基本指标。其计算公式为

式中，分子与分母同属一个总体，分母是分子（标志值）的承担者，即分子与分母具有一一对应关系。例如，一个车间有5名工人，他们的工龄分别是5年、5年、12年、18年、20年，则5名工人的平均工龄为

这种分子与分母的一一对应关系是平均指标与强度相对指标的根本区别所在。强度相对指标的分子与分母是两个不同质的指标之比，没有一一对应关系，如人均GDP、商业网点密度、人口密度等。

同时，算术平均数根据所掌握的资料不同，有简单算术平均数和加权算术平均数两种计算形式。

1）简单算术平均数。简单算术平均数适用于未分组的原始资料，是用变量数列中所有数值求和再除以该组数列的个数而得到的数值平均数。其计算公式为

式中，x1，x2，…，xn表示各个变量值；n表示变量值个数；表示求和符号。

【例4-14】某生产车间有6名工人，若他们的月工资分别为2 000元、2 600元、2 600元、2 800元、2 850元和2 900元，试计算该车间工人的平均月工资。

解：该车间工人的平均月工资为

2）加权算术平均数。加权算术平均数简称加权平均数，适用于总体单位数较多、数据资料已分组的情况。其计算公式为

式中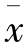，表示算术平均数；x表示各单位标志值（变量值）；f表示各组单位数（项数）；表示权数之和； 表示各组权数占总权数的比重。

【例4-15】某班有50名学生，期末英语考试成绩如表4-8所示，求该班英语考试的平均成绩。

表4-8　某班学生期末英语考试平均成绩计算表

续表

解：根据资料可以计算出

或

即该班英语考试的平均成绩为80.2分。

由加权算术平均数的计算公式可以看出，决定平均数大小的影响因素主要有两个：一是各组变量值（标志值xi），它决定平均数的变动范围；二是各组频数（fi）。频数多的标志值对平均数的影响要大些，频数少的标志值对平均数的影响也相应的小。标志值频数的多少，对平均数的大小有权衡轻重的影响作用，所以称其为权数。但必须指出，权数对于算术平均数的影响作用不是取决于频数本身数值的大小，而是取决于权数比重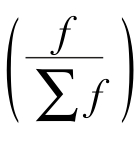的大小。权数比重是指各组单位数占总体单位数的比重，也叫权数系数或相对数权数。哪一组单位数所占比重大，哪一组标志值对平均数的影响就大。当各组的单位数相等或各组单位数所占比重相等时，权数对各组的作用都一样，加权就失去了意义，此时，加权算术平均数等于简单算术平均数。

在计算加权算术平均数时，还会遇到权数的选择问题。选择权数的原则是：务必使各组的标志值与其乘积等于各组的标志总量，并且具有实际的经济意义。一般来说，在分配数列条件下，次数就是权数，但也有例外，特别是用相对数或平均数计算加权算术平均数时，要特别注意。

（2）调和平均数

调和平均数又称倒数平均数，是各变量值倒数的算术平均数的倒数，调和平均数也常被看成算术平均数的变形。在实际工作中，经常会遇到只有各组标志总量和各个组变量值，缺少总体单位数的资料，这时可用调和平均法计算平均数，其计算结果与算术平均数的计算结果完全相同。调和平均数有两种计算方法：简单调和平均数和加权调和平均数。

1）简单调和平均数。简单调和平均数是各单位标志值倒数的简单算术平均数的倒数。其计算公式为

式中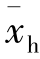，表示调和平均数；x表示各单位标志值（变量值）；n表示总体单位数。

【例4-16】某商品的价格在甲超市为2.0元/公斤[4]，乙超市为2.5元/公斤，丙超市为3.0元/公斤。今在以上超市各用10元购买该商品，求平均价格。

解：根据资料可以算出

2）加权调和平均数。加权调和平均数适用于已分组的资料。如果掌握各组的标志值水平和各组的标志总量，而不知道各组的总体单位数，则应采用加权调和平均数的方法来计算调和平均数。其计算公式为

式中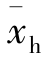，表示调和平均数；x表示各单位标志值（变量值）；m表示权数。

【例4-17】某产品在不同地区的销售情况如表4-9所示，试计算销售的平均价格。

表4-9　某产品在不同地区的销售情况

解：根据资料可以算出

值得注意的是，调和平均数常常作为算术平均数的变形来使用。所以，它的计算内容也和算术平均数一样，是标志总量除以总体单位数。调和平均数的权数是算术平均数中的标志值乘以总体单位数所得的标志总量，即m=xf（m称为权数），将f=m/x代入加权算术平均数公式，可得出两种平均数计算式的关系为

上例中，用加权算术平均数求得的平均价格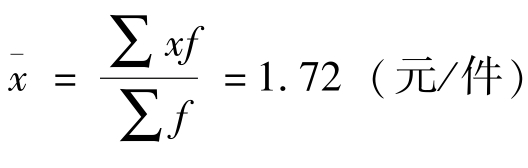：，由此可见，调和平均数是作为算术平均数的变形，虽然它与算术平均数计算方法不同，但其实质是一样的，都是标志总量除以总体总量，所以计算结果也完全一致。一般来说，若掌握的是变量值和总体单位数的资料，则采用算术平均数公式计算平均数；若掌握的是变量值和总体标志总量而缺少总体单位资料，就应采用调和平均数公式计算平均数。

无论是加权算术平均数或加权调和平均数，均存在权数的选择问题。在计算平均数时，若变量值是绝对数，则其次数就是权数。但是，在根据相对数或平均数资料来计算平均指标时，选择权数则需考虑权数与标志值（或标志值的倒数）相乘应具有现实的经济意义，即要选择与标志值存在直接数量关系的资料作权数。

【例4-18】某地10家企业的利润计划完成程度和计划利润额如表4-10所示，试计算利润平均计划完成程度。

表4-10　某地10家企业的利润计划完成程度和计划利润额(www.daowen.com)

解：根据资料可知，利润平均计划完成程度为

运用调和平均数时，应注意几个问题：一是调和平均数是根据变量值倒数求平均数，故变量值不能为0；二是调和平均数和算术平均数一样，易受极端数值影响。若数列中存在极大值，则平均数增大；若存在极小值，则平均数减小。但和算术平均数相比，调和平均数受极端值的影响要小些。

（3）几何平均数

几何平均数是n个变量值连乘积的n次方根，常用于计算平均比率和平均速度。由于掌握的资料的不同，几何平均数分简单几何平均数和加权几何平均数两种。

1）简单几何平均数。简单几何平均数就是n个变量值连乘积的n次方根。其计算公式为

式中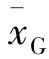，表示为几何平均数；x表示各单位标志值（变量值）；n表示变量值项数。

【例4-19】某地区2012—2016年经济发展速度分别为108％、110％、112％、115％和116％，试计算该地区2012—2016年经济的平均发展速度。

解：根据几何平均数的应用条件，可以计算出

2）加权几何平均数。当计算几何平均数的各个变量的次数不相等时，要应用加权几何平均数。其计算公式为

【例4-20】某人有一笔款项存入银行10年，前2年的年利率为6％，第3～5年的年利率为5％，后5年的年利率为3％。如果按复利计算，则这笔款项的平均年利率为多少？

解：在计算平均年利率时，应首先将年利率加上100％，换算为各年的本利率，然后计算出平均本利率，再减去100％，得到平均年利率，即

在我国统计实务中，几何平均数应用范围较窄，其主要用于计算平均发展速度，属于动态平均数；计算静态平均数时，很少使用此法。在计算几何平均数时应注意，当数列中有一项为0时，不能计算几何平均数。

2.位置平均数

算术平均数、调和平均数和几何平均数都是根据总体全部标志值计算的，均属于数值平均数。在平均指标中，还有根据处于特殊位置上的标志值来确定和计算的位置平均数，即众数和中位数。众数和中位数都不受总体中极端值的影响。假如某现象的次数分布数列不对称，且极端值的影响很大，这时算术平均数或调和平均数会失去代表值的意义。这种情况下，采用中位数和众数就更有代表性。

（1）中位数

将总体中各单位的标志值按大小顺序排列，位于中间位置的标志值就是中位数。中位数将数列的标志值分成两个部分，一半标志值比它小，一半标志值比它大，因而中位数也叫分割值。例如，估计一群人的平均身高，在无测量工具的情况下，则可对人群依高低排队，排在队伍中间的人的身高就可看作平均身高的近似值。

中位数不受极端值的影响，因此在许多场合用它来反映现象的一般水平。例如，某数列为8、10、18、20、30，其中位数是18；若将最大数扩大1 000倍，则中位数仍为18。这说明中位数不受极端值影响。

确定中位数时，必须将总体各单位的标志值按大小顺序排列，最好是编制出变量数列。这里有两种情况：

1）对于未分组的原始资料，需先将标志值按大小排序。设排序的结果为x1≤x2≤…≤xn，则中位数就可以按下面的方式确定，即

2）对于已分组的资料，由组距数列确定中位数。应先按的公式求出中位数所在组的位置，再按下限公式或上限公式确定中位数。

式中，Me表示中位数；L表示中位数所在组下限；U表示中位数所在组上限；fm表示中位数所在组的次数；表示总次数；d表示中位数所在组的组距；Sm-1表示中位数所在组以下的累计次数；Sm+1表示中位数所在组以上的累计次数。

【例4-21】根据表4-11所示数据，计算50名工人日加工零件数的中位数。

表4-11　50名工人日加工零件数

解：由表4-11可知，中位数的位置=50/2=25，即中位数在120～125这一组，L=120，Sm-1=16，U=125，Sm+1=20，fm=14，d=5，从而根据中位数公式可得

应用中位数时应注意，因中位数是它在所有标志值中所处的位置确定的全体单位标志值的代表值，不受分布数列的极大值或极小值影响，故在一定程度上提高了中位数对分布数列的代表性。但有些离散型变量的单项式数列，当频数分布偏态时，中位数的代表性会受到影响。

（2）众数

众数是总体中出现次数最多或最普遍的标志值。它是位置平均数，不受数列中极端变量值的影响，这是区别于算术平均数的一个重要标志。但它与算术平均数的作用一样，也可以反映总体各单位某一数量标志值的一般水平，只是精确度有所区别。

在实际工作中，众数被广泛运用。例如，为了掌握农贸市场某种商品的价格水平，往往利用该种商品最普遍的成交价格为代表；又如，服装、鞋帽等商品的生产和销售，为了满足广大消费者的需要，使这些商品的产销平均协调，有关生产与销售部门就必须了解消费者需求量最大的服装、鞋帽的尺码、规格、型号等，以作为制订生产和销售计划的重要依据；再如，某班40名学生中，20岁的3名，19岁的5名，18岁的29名，17岁的3名，由于18岁的人数最多，故18岁为该班学生年龄标志的众数，它可以代表该班学生年龄的一般水平。

若总体单位数多且有明显集中趋势，则计算众数既方便又意义明确；若总体单位数少，或虽多但无明显集中趋势，就没有众数；若变量数列中有两个或几个变量值的次数都比较集中，就可能有两个或几个众数，这时称为复众数。

确定众数时，首先要将数据资料进行分组，编制变量数列。然后，再根据变量数列的不同种类采用不同的方法。

1）根据单项数列求众数，不需要任何计算，可以直接从分配数列中找出出现次数或频率最高的一组标志值，这就是所求的众数。

2）对组距数列求众数。此时，众数的计算公式有两种，即

式中，f表示众数所在组次数；f-1表示众数所在组前一组的次数；f+1表示众数所在组后一组的次数；L表示众数所在组组距的下限；U表示众数所在组组距的上限；i表示组距。

【例4-22】根据表4-12所示资料，计算众数。

表4-12　某年级某学科学生成绩统计

解：由表4-12可知，众数在80～90这一组，从而有