平均指标是反映社会经济现象一般水平的指标。社会经济现象总体平均水平的变动受两个因素的影响:一是总体内各部分的水平;二是总体的结构,即各部分在总体中所占的比重。平均指标的因素分析就是利用因素分析的方法,从数量上分析总体中各部分水平与总体结构这两个因素的变动对总体平均指标变动的影响。例如,某单位职工总平均工资的变动,取决于各组职工工资水平和各组职工人数在职工总人数中所占比重这两个因素的影响。再如,某公司某项产品总平均单位成本的变动,取决于所属各单位产品成本和成本水平不同的各单位产品产量在总产量中所占比重的影响。
在统计分析中,常常将经济内容相同的不同时期的平均指标数值进行对比,用以反映该经济现象一般水平的变动程度。这种由两个平均指标对比而形成的相对数指标,称为平均指标指数。它的计算公式是
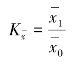
式中,![]() 表示平均指标指数;
表示平均指标指数;![]() 表示报告期平均指标;
表示报告期平均指标;![]() 表示基期平均指标。
表示基期平均指标。
在对总体分组的条件下,总体平均指标可用加权算术平均式计算,即
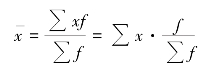
因此
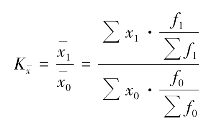
可以看出,总平均指标发生动态变化![]() ,是各组水平x 和各组的总体结构
,是各组水平x 和各组的总体结构![]() 两个因素变动的结果。因此,可利用指数体系分析x 与
两个因素变动的结果。因此,可利用指数体系分析x 与![]() 的变动对总平均数变动的影响。与编制综合指数的原理相似,需引入同度量因素并将其固定在某一期,编制关于x 与
的变动对总平均数变动的影响。与编制综合指数的原理相似,需引入同度量因素并将其固定在某一期,编制关于x 与![]() 的指数,从而形成平均指标指数体系。
的指数,从而形成平均指标指数体系。
一般来说,在编制平均指标指数体系时应遵循两个原则:一是编制关于x 的指数,把同度量因素![]() 固定在报告期;二是编制关于
固定在报告期;二是编制关于![]() 的指数,则把同度量因素x 固定在基期。按照这个原则,平均指标两因素分析的指数体系为
的指数,则把同度量因素x 固定在基期。按照这个原则,平均指标两因素分析的指数体系为
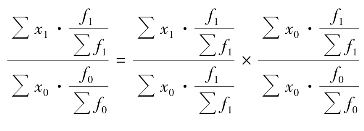
上述公式的指数体系里包括了三个指数,依次称为可变构成指数、固定构成指数和结构影响指数。这三个指数的关系为
可变构成指数= 固定构成指数× 结构影响指数
1.可变构成指数
可变构成指数简称可变指数,反映了总平均指标的变动方向和程度,包含了各组水平x和总体结构![]() 两个因素变动的综合影响。可变构成指数用
两个因素变动的综合影响。可变构成指数用![]() 表示,其表达式为
表示,其表达式为
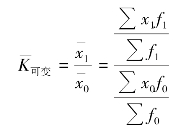
或
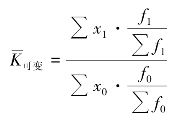
其分子与分母的差额是平均指标的增减变动绝对量,表示为![]() ,或
,或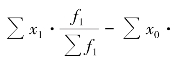
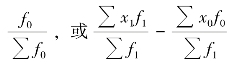 。
。
2.固定构成指数
固定构成指数是将总体结构![]() 固定在报告期而计算的总平均指标指数,消除了总体结构变动的影响,专门反映各组水平x 的变动对总平均指标变动的影响,用
固定在报告期而计算的总平均指标指数,消除了总体结构变动的影响,专门反映各组水平x 的变动对总平均指标变动的影响,用![]() 表示。
表示。
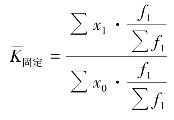
或
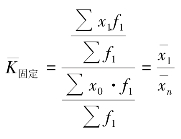
式中,![]() 表示假定的平均指标。(https://www.daowen.com)
表示假定的平均指标。(https://www.daowen.com)
分子与分母的差额表示x 的变动对总平均指标影响的绝对量,表示为![]() 或
或![]()
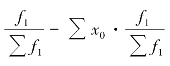 。
。
3.结构影响指数
结构影响指数是将各组水平x 固定在基期而计算的总平均指标指数,用以反映总体结构![]() 的变动对总平均指标变动的影响,用
的变动对总平均指标变动的影响,用![]() 表示。
表示。
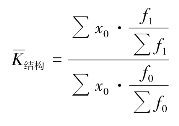
或
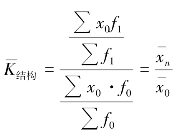
分子与分母的差额表示![]() 的变动对总平均指标影响的绝对量,表示为
的变动对总平均指标影响的绝对量,表示为![]() 或
或![]()
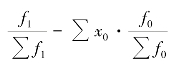 。
。
可变构成指数、固定构成指数和结构影响指数在相对数和绝对量上分别构成下列等式:
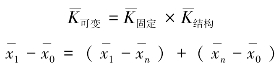
【例10-8】 某企业职工工资如表10-9 所示。请分析总平均工资的变动受职工工资水平和工人结构的变动影响的程度和规模。
表10-9 某企业职工工资
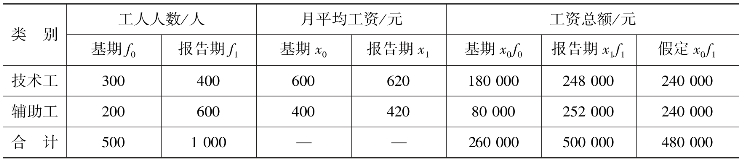
(1)总平均工资的变动分析为

(2)总平均工资受职工工资水平变动影响的分析为
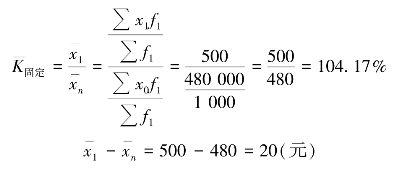
(3)总平均工资受工人结构变动影响的分析为

(4)综合影响分析如下。
相对数分析为
![]()
绝对量分析为
![]()
以上计算结果表明,工资水平上升4.17%,使得总平均工资增加了20 元,但工人结构的变动使总平均工资减少了40 元,两者共同影响的结果是总平均工资下降了3.85%,绝对量减少了20 元。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







