（一）拟合优度的评价

1.多重可决系数

与一元回归模型的拟合优度评价相同，多元线性回归模型的拟合度评价仍然采用可决系数R2，即

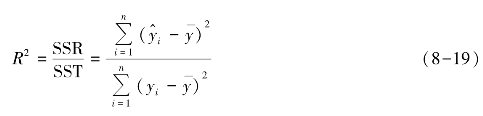
多元回归模型的可决系数称为多重可决系数，是介于0 和1 之间的一个数。R2越接近1，模型对数据的拟合程度就越好。

在样本量一定的条件下，总离差平方和与自变量的个数无关，而残差平方和则会随着方程中自变量个数的增加而减小，因此，R2是自变量个数的非递减函数。在多元线性回归模型中，在比较因变量相同而自变量个数不同的模型的拟合程度时，不能简单地对比多重可决系数，而应采用修正多重可决系数，其计算公式为

由式（8-20）可以看出，当解释变量的个数p ＞1 时，，意味着随着自变量个数增加，将小于R2。

在多元线性回归方程，估计标准误的计算公式为

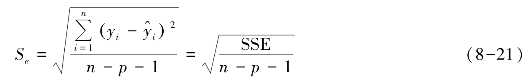
式中，p 是解释变量的个数。估计标准误越小，多元回归方程的拟合度就越好，估计残差就越小。

（二）多元线性回归模型的显著性检验

对多元线性回归模型的显著性检验包括两个方面：一是对整个回归方程的显著性检验（ F 检验）；另一个是对各回归系数的显著性检验（ t 检验）。

1.回归方程的显著性检验

检验所有自变量与因变量之间的线性关系是否显著，利用回归解释平方和SSE 与剩余离差平方和SSR 的比较，应用F 检验来分析二者之间的差别是否显著。(www.daowen.com)

检验步骤有如下四个：

（1）提出假设。H0：β1= β2= … = βp= 0；H1：βi不全为0。

（2）构建F 检验统计量，即方差分析表，如表8-7 所示。

表8-7　F 检验统计量的构建

（3）通过给定的显著性水平α，确定临界值Fα（p，n - p - 1）。

（4）若F ＞Fα（p，n -p -1），则拒绝H0，说明回归参数βi至少有一个不为0，即回归方程是显著的。

2.回归系数的显著性检验

回归方程的线性关系检验通过后，还需要检验每个自变量x 对因变量y 的影响是否显著。理论基础是最小二乘估计的抽样分布，应用t 检验来分析自变量xi对因变量y 的影响是否显著。

检验步骤有如下四个：

（1）提出假设。H0：βi= 0；H1：βi≠0。

（2）构建t 检验统计量。，其中，是最小二乘估计的标准差，也称为标准误差。

（3）通过给定的显著性水平α，确定临界值。

（4）若，则拒绝H0，说明回归参数βi≠0，即某个自变量xi对因变量y 的影响是显著的。