（一）拟合优度的评价

拟合优度是指估计出的样本回归方程（样本回归直线）对样本观测值数据拟合的优劣程度，即样本观测值聚集在样本回归线周围的紧密程度。

1.可决系数

最常用的拟合优度评价指标是可决系数R2，又称判定系数，它是建立在对因变量y 总离差平方和进行分解的基础上的。

在直线回归中，观测值y 的取值大小是上下波动的，但这种波动总是围绕其均值在一定范围内。统计上将y 取值的这种波动现象称为变差，这种变差的产生是由两方面原因引起的。

（1）受自变量变动的影响。

（2）随机因素的影响。

为了分析这两个方面的影响，需要对总的变差进行分解。

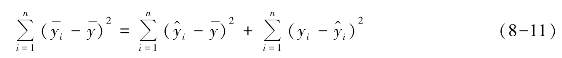
式中，因变量y 的样本观测值与其平均值的离差平方和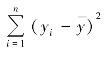称为总离差平方和SST（Total Sum of Squares）；因变量y 的样本估计值与其平均值的离差平方和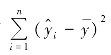称为可解释平方和SSR （Residual Sum of Squares），也可称为回归平方和，是由回归直线做出解释的离差平方和；因变量y 的样本观测值与估计值之差的平方和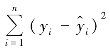称为残差平方和SSE （Explained Sum of Squares），是回归线未做出解释的离差平方和。可以证明，SST=SSR+SSE。

显然，在总的离差平方和中，回归解释的平方和所占的比重越大，则回归效果越好，说明回归直线与样本观测值拟合得好；如果残差平方和所占的比重大，则回归直线与样本观测值拟合得不理想。把回归解释平方和与总离差平方和之比定义为可决系数（判决系数）R2。

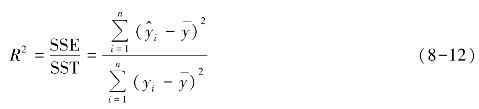
可决系数是对回归模型拟合程度的综合度量，可决系数越大，回归模型拟合程度越高。R2表示全部偏差中有百分之几的偏差可由x 与y 的回归关系来解释。可决系数具有非负性，取值范围为0 到1 之间，即0≤r2≤1，r2越接近1，说明回归方程对样本观测值的拟合效果越好；反之，则越差。在一元线性回归中，可决系数在数值上是简单相关系数的平方，即R2=r2。

2.估计标准误差

估计标准误差也称为估计标准差或估计标准误，也是用来反映估计出的回归方程对实际样本观测值拟合优度的指标。估计标准误差越大，说明估计的回归方程的拟合度越差。

（1）估计标准误差的计算方法。

估计标准误差是因变量的实际值与估计值的残差的平均数。其定义公式为

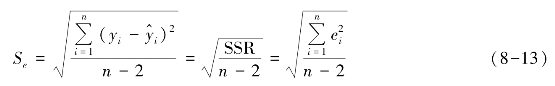
式中，Se表示估计标准误差；SSR 是残差平方和；ei是估计残差；n -2 是自由度；n 是样本观测值个数；2 是一元线性回归中要估计的回归个数。式（8-13）除以自由度n -2 的原因是想得到对随机误差项ε 的标准差σ 的无偏估计。回归估计标准误差Se不仅可以衡量样本回归方差的拟合效果，更是回归预测所必须了解的一个指标。Se越小，平均来看回归估计的误差就越小。对预测来说，只要影响变量的因素没有重大变化，Se越小，预测误差通常也会越小。

（2）估计标准误差与相关系数的关系。

根据相关系数和估计标准误差的计算公式可以推导出二者之间的如下关系式：

(www.daowen.com)

式中 r——相关系数；

σy——因变量的标准差；

Se——估计标准误差。

从以上公式可以看出，r 与Se的变化方向相反，r 越大，Se就越小，表明变量间的相关关系越密切，估计的回归方程拟合优度就越高；r 越小，Se就越大，表明变量间的相关关系越不密切，估计的回归方程对样本观测值的拟合优度就越低。

（二）一元线性回归模型的显著性检验

对线性回归模型的显著性检验包括两个方面：一个是对整个回归方程的显著性检验（ F检验）；另一个是对各回归系数的显著性检验（ t 检验）。就一元线性回归模型而言，上述两个检验是等价的。

1.回归方程的显著性检验

检验自变量与因变量之间的线性关系是否显著，利用回归解释平方和SSE 与剩余离差平方和SSR 的比较，应用F 检验来分析二者之间的差别是否显著。

检验步骤有如下四个：

（1）提出假设。H0：β = 0；H1：β ≠0。

（2）构建F 检验统计量，即方差分析表，如表8-6 所示。

表8-6　F 检验统计量的构建

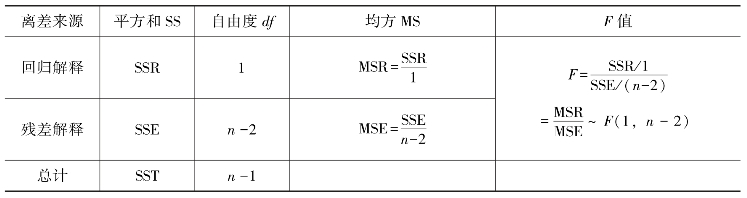
（3）通过给定的显著性水平α，确定临界值Fα（1，n - 2）。

（4）若F ＞Fα（1，n - 2），则拒绝H0，说明回归参数β ≠0，即回归方程是显著的。

2.回归系数的显著性检验

检验自变量x 对因变量y 的影响是否显著，理论基础是最小二乘估计b 的抽样分布，应用t 检验来分析自变量x 对因变量y 的影响是否显著。

检验步骤有如下四个：

（1）提出假设。H0：β = 0；H1：β ≠0。

（2）构建t 检验统计量。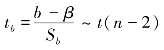，其中，Sb是最小二乘估计b 的标准差，也称为标准误差。

（3）通过给定的显著性水平α，确定临界值。

（4）若，则拒绝H0，说明回归参数β ≠0，即自变量x 对因变量y 的影响是显著的。