(一)估计的回归方程
设有两个变量x 与y,x 是可以控制的变量,作为自变量;y 表示因变量,即随机变量。取x 的n 个样本观测数值x1,x2,…,xn,通过试验或观测得到y 的n 个样本观测值y1,y2,…,yn。习惯上,把( xi,yi)( i = 1,2,…,n)统称为样本观测值。
为了对一元线性回归方程中的参数α 和β 进行估计,我们把这n 对数据( x1,y1),( x2,y2),…,( xn,yn)描绘在直角坐标系中,即为相关图,又称散点图,如图8-1 所示。从图中可以看出,这些点大体在一个带形区域内,即x 与y 呈简单的线性相关关系。假设它们之间有如下关系:
![]()
式中,![]() 表示对y 的期望值E(y)的回归估计值或拟合值;a 和b 是对一元线性回归模型中的参数α 和β 的估计,式(8-6)称为一元线性经验或估计的回归方程,在图形中表示为样本回归直线。
表示对y 的期望值E(y)的回归估计值或拟合值;a 和b 是对一元线性回归模型中的参数α 和β 的估计,式(8-6)称为一元线性经验或估计的回归方程,在图形中表示为样本回归直线。
其实,![]() 不仅可以作为y 的期望值E(y)的回归估计值,也可以作为y 的估计值。y 与
不仅可以作为y 的期望值E(y)的回归估计值,也可以作为y 的估计值。y 与![]() 的偏差称为残差项,用e 表示,则
的偏差称为残差项,用e 表示,则![]() ,残差项e 可以当作对随机误差项ε 的估计。
,残差项e 可以当作对随机误差项ε 的估计。
(二)参数α 和β 的最小二乘法估计
通常采用最小二乘法的原理,计算得到回归模型参数α 和β 的估计值a 和b。
根据最小二乘法原理,实际观测值y 与估计值![]() 的残差平方和等于最小值,即
的残差平方和等于最小值,即
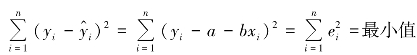 。
。
由二元函数极值原理有下列标准方程组成立:
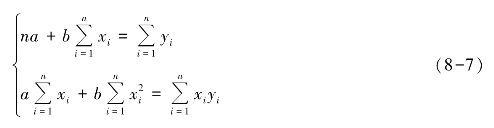
记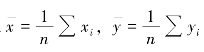 ,则上面的方程组变为
,则上面的方程组变为
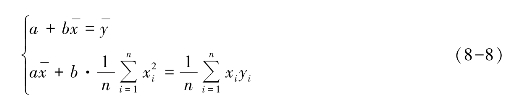
求解此方程组可得
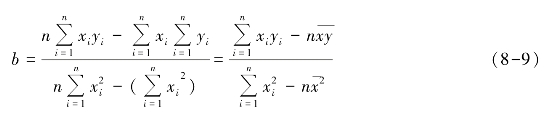
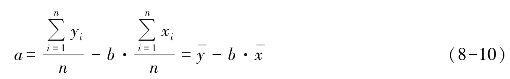 (https://www.daowen.com)
(https://www.daowen.com)
式中,a 和b 是对一元线性回归模型中的参数α 和β 的估计,![]() 和
和![]() 分别为样本观测值xi和yi的平均值。
分别为样本观测值xi和yi的平均值。
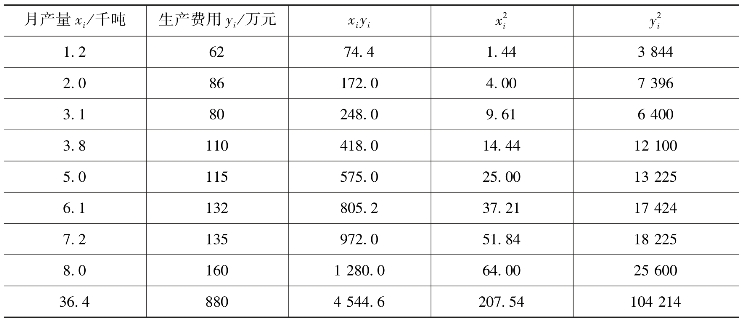
【例8-5】 某地区8 个企业生产产品的月产量和生产费用,以及确定回归方程所需数据资料如表8-5 所示。
(1)计算该地区生产产品产量与生产费用之间的相关系数,说明二者之间的相关程度及方向。
(2)根据表中资料配合该地区企业生产产品产量与生产费用推导估计的一元线性回归方程。
(3)如果下年度该地区生产产品的月产量为9 千吨,请预测其生产费用。
表8-5 某地区8 个企业月产量和生产费用
(1)该地区生产产品产量与生产费用之间的相关系数为

计算结果说明,该地区产品生产产量与生产费用之间存在高度的正相关关系,可以采用一元线性回归模型。
(2)一元线性估计的回归方程为![]() 。
。
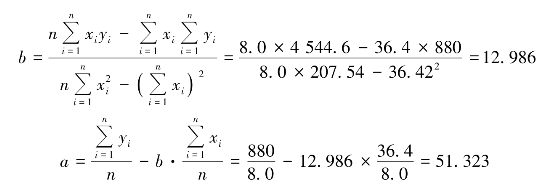
因此,估计的直线回归方程为
![]()
回归方程的经济意义是,当月产量每增加1 千吨时,生产费用平均增加12.896 万元。
(3)利用估计的回归方程可以进行预测,如果该企业下一年月产量为9 千吨,在其他条件相对稳定时,其生产费用将达到![]() 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







