（一）相关系数的范围及判定标准

线性相关关系的密切程度是通过相关系数来测量的。相关系数是在直线相关的条件下说明两个现象之间相关关系密切程度的统计分析指标，通常用r 表示。

相关系数的取值范围在-1 到+1 之间，即-1≤r≤+1，或。越接近于1，表明相关的密切程度越高；越接近于0，表明相关的密切程度越低。r 的符号表示相关的方向，r 为正，表示正相关关系；r 为负，表示负相关关系。下面用图示的方法加以说明。

（1），表示变量之间是完全的线性相关关系。其中，r=1 表示完全正相关，如图8-2 所示；r=-1 表示完全负相关，如图8-3 所示。

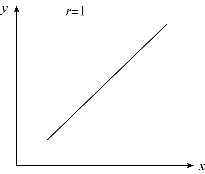
图8-2　完全正相关

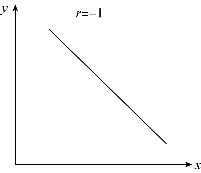
图8-3　完全负相关

（2）r=0，表示变量之间完全无线性相关关系，如图8-4 所示。但并不表示变量之间不存在其他非线性的相关关系。

图8-4　无线性相关

（3），表示变量之间是不完全相关关系。其中，0＜r＜1 表示变量之间是不完全正相关，如图8-5 所示；-1＜r＜0 表示变量之间是不完全负相关，如图8-6 所示。

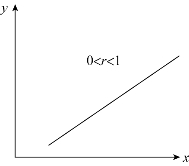
图8-5　不完全正相关

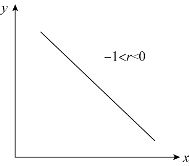
图8-6　不完全负相关

在根据r 取值判定相关关系的密切程度时，通常的划分标准为，视为无线性相关；在0.3 ～0.5，视为低度线性相关；在0.5 ～0.8，视为显著相关；在0.8 以上，则是高度的密切相关。

（二）相关系数的计算

根据相关系数的定义，可按以下公式计算：(www.daowen.com)

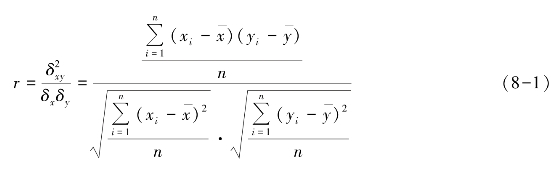
式中 n——资料项数；

——x 变量数列的算术平均数；

——y 变量数列的算术平均数；

δx——x 变量数列的标准差；

δy——y 变量数列的标准差；

δxy——x、y 两个变量数列的协方差。

将式（8-1）的分子、分母同时约掉公因子，则公式变形为

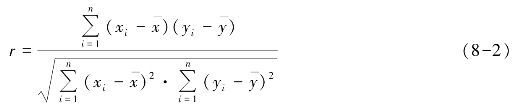
由于相关系数是通过将各个离差相乘来说明现象之间的线性相关程度的，因此这种方法通常也被称为“积差法”。

按定义公式计算相关系数的过程运算量大，计算烦琐。因此，在实际分析中多采用由定义公式推导出的简捷公式计算相关系数。其简捷公式为

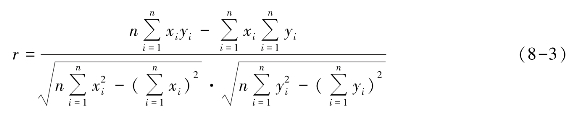
按照式（8-3）计算相关系数，只需计算出xy、x2、y2就可以了，大大简化了运算过程。通常通过列表的方式计算xy、x2、y2。下面举例说明r 的计算方法。

【例8-4】　某地7 个企业的工业总产值、税利总额及相关系数计算的有关数据如表8-4所示。

表8-4　相关系数计算

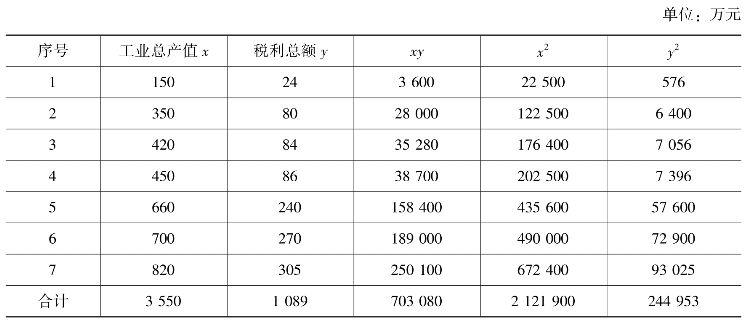
根据表8-4 所列数据，计算相关系数如下。

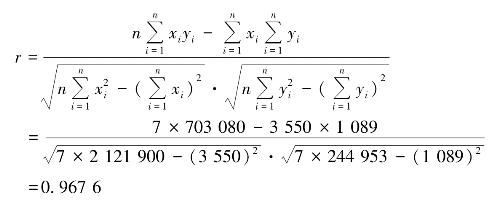
据此可判断工业总产值x 与税利总额y 有高度的线性相关关系。