（一）总体方差已知的假设检验

设总体X ～N（0，1），总体方差σ2为已知，（x1，x2，…，xn）为总体的一个样本，样本平均数为。现在的问题是对总体均值μ 进行假设检验。H0：μ =μ0（或μ ≤μ0，μ ≥μ0）。

根据抽样分布定理，样本平均数为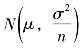，如果H0成立，检验统计量z 及其分布为

检验统计量z 服从均值为0、方差为1 的标准正态分布。

根据已知的总体方差、样本容量n 和样本平均数，计算出检验统计量z 的值。对于给定的检验水平，查正态分布表可得临界值，将所计算的z 值与临界值比较，便可得出检验结论。

1.双侧检验

在正态分布中，的概率很小，只有大小。例如，，临界值，则的概率只有5%。从总体中抽取一个样本，计算值，如果该值是大于1.96 的，则小概率事件发生了，有理由认为该样本不是抽取自假设的总体，所以拒绝原假设。综上所述，双侧检验中的决策规则为

当时，拒绝原假设H0；

当时，接受原假设H0。

【例7-1】　某医院想了解患者的候诊时间与以往相比是否发生了显著变化。往年的情况是，平均每个患者的候诊时间是40 分钟，方差为400 分钟，现在抽取100 名患者进行调查，其平均候诊时间为45 分钟。试帮助医院做出决策。（ α = 0.01）

解：根据题意建立假设。

H0∶μ = 40;H1∶μ ≠40。

总体方差σ2已知，选择z 作为检验统计量。

α = 0.01，查标准正态分布表可知z 的临界值。

因为，所以接受原假设，即该医院患者候诊的时间无显著变化。

2.单侧检验

（1）左侧检验。在正态分布中，z ≤zα的概率很小，只有α 大小。例如，α =0.05，临界值- zα=- 1.645，则z ≤- zα的概率只有5%。若某次抽取样本所计算的z 值是小于-1.645的，则小概率事件发生了，所以拒绝原假设。即左侧检验的决策规则为

当z ≤- zα时，拒绝原假设H0；

当z ＞- zα时，接受原假设H0。

（2）右侧检验。在正态分布中，z ≥zα的概率很小，只有α 大小。例如，α =0.05，临界值zα=1.645，则z ≥1.645 的概率只有5%。若某次抽取样本所计算的z 值是大于1.645 的，则小概率事件发生了，所以拒绝原假设。即右侧检验的决策规则为

当z ≥zα时，拒绝原假设H0；

当z ＜zα时，接受原假设H0。(www.daowen.com)

【例7-2】　根据过去大量资料可知，某厂生产产品的使用寿命服从正态分布N （1 020，1002）。现从最近生产的一批产品中随机抽取16 件，测得样本平均寿命为1 080 小时。试在0.05 的显著性水平下判断这批产品的使用寿命是否有显著提高。

解：根据题意，提出假设。

H0∶μ ≤1 020;H1∶μ ＞1 020。

检验统计量；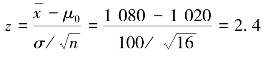

查表得临界值zα=1.645。

由于z =2.4＞zα=1.645，因此应拒绝H0而接受H1，即这批产品的使用寿命确有显著提高。

（二）总体方差未知的假设检验

设总体X ～N（μ，σ2），但总体方差σ2未知，检验统计量z 中包含了未知参数σ，此时对总体均值的检验不能与上述检验相同。为了得到一个不含未知参数的检验统计量，很自然会用总体方差的无偏估计量——样本方差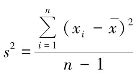来代替总体方差σ2。此时，样本平均数服从期望为μ、方差为s2/n、自由度为n -1 的t 分布，因此可以选择t 作为检验统计量，计算公式为

根据题意提出假设，构造检验统计量t，并根据样本信息计算其具体值；对于给定的检验水平α，由t 分布表查得临界值；将所计算的t 值与临界值比较，得出检验结论。

双侧检验时，若，则拒绝H0。

左侧检验时，若t ≤- tα，则拒绝H0。

右侧检验时，若t ≥tα，则拒绝H0。

【例7-3】　从长期的资料可知，某厂生产的某种电子元件服从均值为200 小时、标准差未知的正态分布。通过改变部分生产工艺后，抽得10 件为样本，数据（小时）为202，209，213，198，206，210，195，208，200，207。试在0.05 的显著性水平下判断在新工艺下，这种电子元件的平均值是否有所提高。

解：根据题意，可建立如下假设。

H0∶μ ≤200;H1∶μ ＞200。

根据已知数据求得。

检验统计量。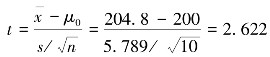

由α =0.05，查表得临界值tα（n - 1）= t0.05（10 - 1）= 1.833 1。

由于t=2.622 ＞tα（n -1）=1.833 1，因此拒绝H0接受H1，即可以接受“在新工艺下，这种电子元件的平均值有所提高”的假设。

t 检验统计量适用于小样本且总体方差未知的情况下对正态总体均值的假设检验。随着样本容量n 的增大，t 分布趋近于标准正态分布。所以在大样本（n＞30）且总体方差未知时，对正态总体均值μ 的假设检验通常近似采用z 检验统计量。同理，在大样本情况下对非正态分布总体均值的检验也可用z 检验统计量。这时，根据大样本的抽样分布定理，总体分布形式不明或为非正态总体时，样本平均数趋近于正态分布。检验统计量z 中的总体标准差σ 用样本标准差S 来代替。