抽样组织方式是在抽取样本时，对总体各单位的一种组织安排，简称抽样方式。抽样组织方式有简单随机抽样、类型抽样、等距抽样和整群抽样。不同的抽样方式会产生不同的抽样效果，应当根据被研究现象总体的特征认真选择与确定合适的抽样组织方式。

（一）简单随机抽样

简单随机抽样方式涉及的有关问题我们已作了详细论述。作为对总体各单位的一种组织安排，这里要强调的是，在抽取样本之前，应该先确定总体范围，并对总体中的每个单位进行编号，形成明确的抽样框。编入抽样框的总体单位称为抽样单位（亦称抽样单元），因而抽样框是能从中进行随机抽样的所有抽样单位的名单或清册。有了抽样框，就便于使用随机数码表或其他随机形式从总体中抽取样本单位。

根据抽样单位的具体情况和抽样组织的要求，抽样单位可以分成若干级别。其中，作为调查资料直接承担者的抽样单位（一般为最低一级抽样单位）称为基本抽样单位。例如，对某居民区居民家庭室内装修费用情况进行抽样调查，假设该居民区共有30 幢居民楼，每幢楼居住70 户居民。为了使被抽中的居民户在总体中的分布是均匀的，在抽样时先从30 幢居民楼中随机抽取6 幢，然后从抽中的6 幢楼中再随机地各抽取7 户家庭，调查其室内装修费用。则每幢居民楼就是一个一级抽样单位，每户居民家庭就是一个二级抽样单位。这里，居民家庭是调查资料的直接承担者，亦即基本抽样单位。这样可以有效地提高样本的代表性。

（二）类型抽样

类型抽样又称分层抽样或分类抽样，是统计分组法与抽样法的结合。其特点是先将总体各单位按主要标志进行分组，然后从各组中按照随机原则抽取一定数量的单位组成样本。

设总体由N 个单位组成，按主要标志将其划分成h 组（h=1，2，3，…，k），使N=N1+N2+…+Nk。然后从每组（即从Nh）中随机抽取Nh个单位组成容量为n 的样本，使n=n1+n2+…+nk。这种抽样方式称为类型抽样。其中，nh称为组样本容量，n 称为全样本容量。

类型抽样便于组织，实施时应当准备好关于各组的抽样框。由于抽样是在各组独立进行的，因此允许根据不同的情况灵活地采用不同的抽样方法。根据组样本资料计算的组平均数或组样本成数Ph，可以用来对该组的参数进行估计，将其汇总成全样本平均数或全样本成数p，用以估计总体平均数或总体成数等时，汇总的方法又很简单。与简单随机抽样比较，类型抽样的样本在总体中的分布更加均匀，因而抽样误差明显小于简单随机抽样。

由于类型抽样是按照随机原则分别从各组中抽取一定数量的单位组成样本，而各组的总体单位不同，因此通常是按一定比例从各组中抽取样本单位的，即

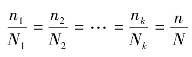
因此，各组的样本单位数nh可根据下式确定：

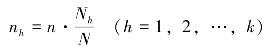
类型抽样的样本平均数与样本成数Pst可分别按下列公式计算：

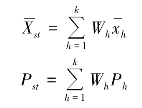
其中，为第h 组的样本平均数；Ph为第h 组的样本成数；Wh为第h 组单位数占全部单位数的比重，即权数。在按比例抽样时有

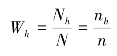
样本平均数的抽样平均误差可按下列公式计算：

采用重复抽样方法时，的计算公式为

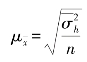
采用不重复抽样方法时，的计算公式为

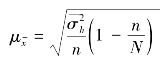
其中，为各组内方差的加权算术平均数，其计算公式为

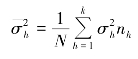
在取得抽样资料的情况下，总体方差可以用样本组内方差的加权算术平均数代替，即在计算抽样平均误差时，总体方差可用下式计算的结果代替，即

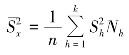
样本成数Pst的抽样平均误差可按下列公式计算：

采用重复抽样方法时，μp的计算公式为

采用不重复抽样方法时，μp的计算公式为

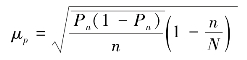
其中，为各组内方差Ph（1 - Ph）的加权算术平均数。在取得抽样资料的情况下，可以用样本组内方差的加权算术平均数代替，即用下式计算的结果代替：

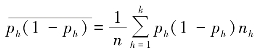
【例6-11】　某市进行居民家庭收入调查，分城镇居民和农村居民两部分抽样。在43 560户城镇居民中随机抽取300 户，在145 200 户农村居民中随机抽取1 000 户。调查结果为城镇居民年平均户收入16 280 元，标准差为4 120 元；农村居民年平均户收入11 080 元，标准差为2 546 元。以95.45%的置信度估计全市年平均户收入。

设N1=43 560，N2=145 200，则N=N1+N2=188 760

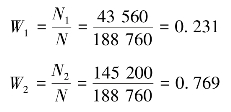(www.daowen.com)

故

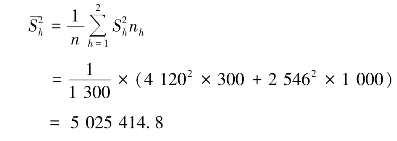
则。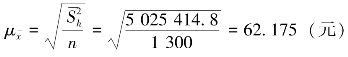

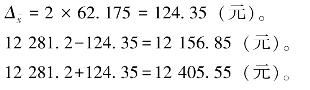
故全市年平均户收入在12 156.85 ～12 405.55 元，做出这种估计的把握为95.45%。

在从各组中抽取样本单位时，若各组总体单位数目差别不大，亦可采用不等比例抽样。

（三）等距抽样

等距抽样又称为机械抽样或系统抽样。它是事先将总体各单位按某一标志排列，然后按固定的顺序和间隔来抽取样本单位的一种抽样组织方式。

若从总体N 个单位中抽取n 个单位组成样本，可先将N 个单位按一定标志排队，然后将N 个单位划分为n 个相等的部分，每个部分包括K 个单位，即。在实施抽样时，先从第一部分顺序为1，2，…，r，…，K 的单位中随机地抽取一个单位r，而在第二部分中抽取顺序号为r+k 的单位，在第三部分抽取顺序号为r+2K 的单位，…，在第n 部分抽取顺序号为r+（n-1）K 的单位，共n 个单位组成一个样本，各样本单位之间的间距均为K，K 称为抽样间距。等距抽样的随机性体现在第一个样本单位的抽取上。当第一个单位的位次确定后，其他样本也就随之确定了。

用来作为排列总体各单位顺序依据的标志，可以是与所研究变量数值大小无关或不起主要影响作用的标志，称之为无关标志；也可以是与变量数值大小保持密切联系或起主要影响的标志，称为有关标志。按无关标志排队的等距抽样与简单随机抽样的原理类似，抽样平均误差的计算可采用简单随机抽样的方法。但由于在一定的间距内只抽取一个样本单位，故其抽样平均误差需按不重复简单随机抽样方法计算。按有关标志排队的等距抽样实质上体现了类型抽样的一些特点，一般在抽取第一个样本单位时，取第一部分处于中间位置的变量值，则可以有效地提高样本的代表性。按有关标志排队等距抽样时，抽样平均误差的计算方法可参照类型抽样。

按等距抽样方式抽取样本单位，能够使样本单位均匀地分配在总体中。因此，等距抽样的误差一般较简单随机抽样要小一些。但应注意到，等距抽样在排定顺序、确定第一个样本单位的位次后，其余单位的位次也随之确定了，因此要避免抽样间距与现象本身的周期性节奏相重合而引起的系统性影响，以防止发生系统性偏差，影响样本的代表性。

（四）整群抽样

整群抽样是将总体各单位划分成若干群，再按照随机原则从中抽取一些群组成样本，调查时则对样本群中的所有单位进行全面调查的一种抽样组织方式。

设总体N 个单位可以划分为R 群，每群包含M 个单位。从总体R 群中随机抽取r 群组成样本，对中选的rM 个单位进行调查。样本的第i 群第j 个单位的标志值为Xij，第i 群的样本平均数为

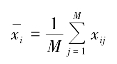
则样本平均数为

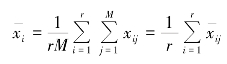
从上式不难看出，整群抽样实质上是以群代替总体单位，以群平均数代替总体单位标志值之后的简单随机抽样。因此，样本统计量的抽样平均误差μ 也可以按不重复简单随机抽样方法来计算。

在整群抽样中，总体方差可以用群间方差δ2代替。若从以往全面调查资料得知各群平均数为，总体平均数为，则可用算式

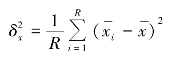
求出总体群间方差以代替总体方差。当缺乏全面调查资料时，可按

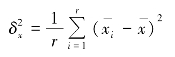
计算出样本群间方差以代替总体方差。则样本平均数的抽样平均误差为

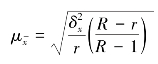
同理可得，样本成数的抽样平均误差为

【例6-12】　对某居民小区居民食品消费量进行抽样调查，以每个楼层为群进行整群抽样，每个楼层都有8 户居民。简单随机地从全部510 个楼层中抽取12 个楼层，对抽中的96户居民调查，资料如表6-6 所示。

表6-6　12 个楼层96 户居民人均月食品消费金额

表6-6 中，代表抽中的楼层中8 户居民人均月食品消费金额。依题意知，R=510，r=12，M=8，则样本平均数为

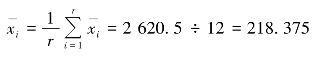
样本群间方差为

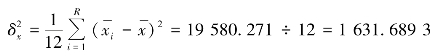
则其抽样平均误差为