（一）区间估计的意义

点估计是用样本统计量的某一具体值来估计总体参数的值。这个值可能等于总体参数的值，也可能不等于总体参数的值。二者只是在平均意义上相等。例如，从表6-1 和表6-2可见，总体平均数，而在其全部25 个可能样本平均数中，样本平均数的只有说明样本平均数等于总体平均数的概率为，而的概率为。由此可见，所谓优良估计量（即无偏、一致和有效的估计量）并不能百分之百地保证统计量的取值等于总体参数的值。由表6-2 还可知，，即总体平均数居于14 ～18 的概率是。

在抽样法中，我们常常用一个区间及其出现的概率来估计总体参数，这种方法称为区间估计。具体地说，区间估计是用统计量和它的抽样平均误差构成的区间来估计总体参数，并以一定概率保证总体参数将落在所估计的区间内。这一概率保证程度称为抽样估计的置信度，这一区间称为抽样估计的置信区间。

（二）总体平均数的区间估计

1.大样本条件下总体平均数的置信区间

由样本平均数的抽样分布可知，如果总体服从正态分布或n＞30，且总体方差已知，则有

其中，为标准正态分布的上分位数。对一个服从正态分布的随机变量X ～N（0，1），α ∈（0，1），若实数zα满足P{X ＞zα} = α，则zα称为标准正态分布的上α 分位点。

因为标准正态分布随机变量为

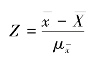
所以有

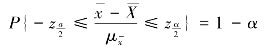
从而可得

其中，1-α 是置信度，一般用F（Z）表示。它说明在随机抽样时，用于估计总体平均数X落在区间之间的概率是1-α，因此α 就是总体平均数不在这一区间的概率。所以称为当置信度为1-α 时的置信区间。

置信区间包含两层含义。就其概率意义而言，对于来自正态总体的所有样本，若用上述公式确定它们的置信区间，则有100（1-α）%的置信度将总体平均数包括在该区间之内。就其实践意义而言，对于某一个来自正态总体的样本，有100（1-α）%的把握说该样本的置信区间将总体平均数包括在内，也可能没有包括，所以一个置信区间包括的把握性只有100（1-α）%。置信度为95%的置信区间（α=5%）如图6-1 所示。

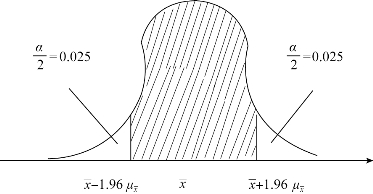
图6-1　置信度为95%的置信区间（α=5%）

在图6-1 中，标准正态曲线下阴影部分的面积占标准正态曲线与横轴围成的总面积的95%，表明用样本平均数估计总体平均数的置信度时，F（Z）=100（1 -α）% =95% 。横轴上标明的区间表示用样本平均数估计总体平均数有95%把握性的置信区间，其中，。

【例6-8】　沿用【例6-3】　和【例6-5】　的资料和计算结果，该居民区样本户均用电量为125 kW/h，样本标准差为35 kW/h。

若采用重复简单随机抽样方法，样本平均数的抽样平均误差，抽样极限误差，概率度，抽样估计的置信度F（Z）= F（2）= 95.45% 。所以，以95.45%的把握，用样本户均用电量估计该区全部居民户均用电量的置信区间为

说明有95.45%的把握估计全区居民户均用电量在118 ～132 kW/h。

若采用不重复简单随机抽样法，则，概率度，F（Z）=F（2.01）=95.56% 。此时，以95.56%的把握，用样本平均数x估计总体平均数的置信区间为

说明以95.45%的把握估计该区居民户均用电量在118 ～132 kW/h。

通过本例可知，在抽样估计的置信区间相同（即抽样估计的准确性要求相同）时，不重复抽样方法比重复抽样方法的置信度高。同理可知，在抽样估计的置信度相同时，采用不重复抽样方法比重复抽样方法的置信区间要小，即准确性要高一些。

需要说明的是，本例中虽然总体方差是未知的，但由于n=100＞30，因此可以用样本标准差代替总体标准差去计算抽样平均误差。

2.小样本条件下正态总体方差未知时，总体平均数的区间估计

根据样本平均数的分布定理可知，当n＜30，且正态总体的方差未知时，有

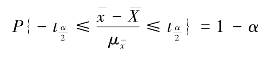
其中，为t 分布的上分位数。

因为小样本统计量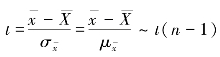，且由于总体方差未知，在计算或时，需要用样本方差估计总体方差。而作为总体方差无偏估计量的样本方差为

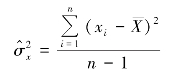
因而有

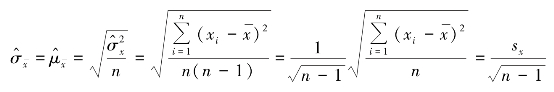(www.daowen.com)

所以，可以变换为

或者

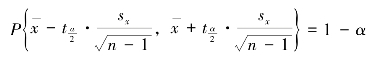
在上述条件下，对未知的总体平均数，其置信度为100（1 - α）%的置信区间是

或者

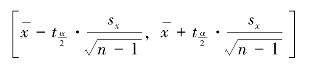
【例6-9】　某公司的股票价格服从正态分布，为了掌握该公司股票的平均价格，随机地对其26 天的交易价格进行调查。结果表明，平均价格为35 元，标准差为2 元。以98%的置信度求该公司股票平均价格的置信区间。

根据上述资料可知，n=26 （小样本），样本标准差Sx=2 元，样本平均数。所以，总体方差的估计值（即样本的调整方差）为

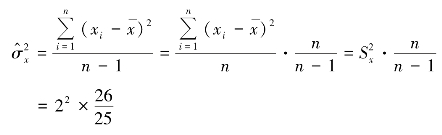
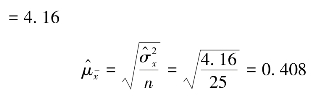
查t 分布表，当α /2=0.01，自由度df=26-1=25 时，，t=-2.485。根据置信区间的计算公式，该公司股票平均价格的置信区间为

以上结果表明，有98%的把握估计该公司股票价格在33.986 ～36.014 元。

（三）总体成数的区间估计

根据样本成数的抽样分布定理，当np ＞5，n（1 - p）＞5 时

因为

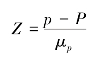
所以

则置信度为1-α 的总体成数的置信区间为

根据点估计理论可知，样本成数p 是总体成数P 的优良估计量。因此，在计算抽样平均误差μp时，如果总体方差p（1 - P）未知，我们可以用样本方差p（1 - p）代替总体方差，或者使用P（1 - P）的最大值0.25 来计算μp。

【例6-10】　沿用【例6-4】　资料，已知n=100，np=94，n（1 -p）=6，样本合格率p=0.94。求产品合格率的置信区间（置信度为95.45%）。

采用重复简单随机抽样时，抽样平均误差μp=0.023 75，则产品合格度的置信区间为

上述结果表明，有95.45%的把握该产品的合格率在89.25% ～98.75%。

采用不重复简单随机抽样时，抽样平均误差μp=0.023 51，则产品合格率的置信区间为

若以P（1 - P）= 0.25 代替总体方差，采用重复简单随机抽样时，抽样平均误差为

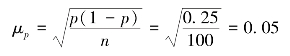
则产品合格率的置信区间为