(一)总体平均数的点估计
点估计就是以样本统计量直接估计总体未知参数,即以样本统计量的具体值作为总体参数的估计值。
如果总体平均数![]() 是个未知数,根据随机样本的数据可以计算出样本平均数
是个未知数,根据随机样本的数据可以计算出样本平均数![]() ,则样本平均数的具体值就是总体平均数的点估计值。当n 足够大时,由于样本平均数
,则样本平均数的具体值就是总体平均数的点估计值。当n 足够大时,由于样本平均数![]() 具备优良估计的三个标准,因此样本平均数的具体值是总体平均数的优良点估计值。
具备优良估计的三个标准,因此样本平均数的具体值是总体平均数的优良点估计值。
例如,在【例6-3】 中,为了了解某月该居民区全部居民的户均用电量,随机抽取100户居民调查,得出户均用电量为125 kW/h (样本平均数),则可以将其作为该区全部居民户均用电量(总体平均数)的点估计值,估计该区全部居民户均用电量为125 kW/h。又如,为了了解城市居民的消费水平,随机地从全部城市居民中抽取1 000 户居民调查,得出某年人均消费金额为3 200 元,据此可得出全部城市居民某年人均消费金额的点估计值为3 200 元。
(二)总体成数的点估计
当n 足够大时,由于样本成数p 是总体成数P 的优良估计量,因此当总体成数未知时,可以用样本成数p 的值作为总体成数P 的点估计值。
例如,在【例6-4】 中,为了了解5 000 件产品的合格率,随机抽取100 件产品调查,得出样本合格率为94%,可据此得出5 000 件产品的合格率的点估计值亦为94%。(https://www.daowen.com)
【例6-7】 某公司考虑购买一批减价商品,共2 000 件,其中有些是次品,但不知次品数或次品率是多少。但该公司知道每件次品的修复成本为0.25 元,并认为若总的修复成本低于50 元,则购买这批商品是有利可图的。在购买前,该公司随机地从中抽取100 件商品进行调查,发现8 件是次品。试估计这批商品的次品率,并判断该公司是否可以购买这批商品。
设样本次品率为p,则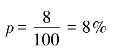 。用样本成数p 作为总体成数P 的点估计值,则这批商品的次品率亦为8%。
。用样本成数p 作为总体成数P 的点估计值,则这批商品的次品率亦为8%。
又因为这批商品总数N=2 000,所以该批商品中的次品数为NP=2 000×8% =160 (件)。所以该批商品所需要的总修复成本为0.25×160=40 (元)。由此可见,该公司可以购买这批商品。
(三)总体方差的点估计
一般地,设某总体方差![]() 是个未知数,当从该总体中随机抽取一个容量为n 的样本时,样本方差
是个未知数,当从该总体中随机抽取一个容量为n 的样本时,样本方差![]() 是总体方差的无偏估计量,即
是总体方差的无偏估计量,即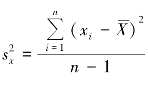 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







