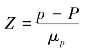样本成数的抽样分布定理：对于任意一个数学期望为P、方差为P（1 - P）的二项式分布总体，当n 足够大（一般地，nP ＞5；n（1 -P）＞5）时，样本成数p 趋于服从数学期望为P、方差为的正态分布，标准化随机变量趋于服从标准正态分布。

当样本取自无限总体或采用重复抽样方法时

当采用不重复抽样方法，且样本取自有限总体时

这是中心极限定理的推论之一。

当我们需要研究属性总体中具有某种特征的单位占总体的比重时，则总体服从二项分布。中心极限定理的上述推论成为我们利用正态分布函数表解决这类抽样估计问题的理论依据。

标准化随机变量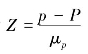中的p-P 是某一具体样本成数p 与总体成数P 的离差，即抽样误差，作为表示抽样误差可能范围的抽样极限误差，所以上式又可表示为(www.daowen.com)

从而可以根据抽样估计的准确性要求Δp和已计算出的抽样平均误差μp的值来计算Z 值，然后从标准正态分布函数表中查出与之对应的概率值，即得出抽样估计的置信度。

【例6-6】　沿用【例6-4】　资料，因为n=100，p=0.94，有np=100×0.94=94，n（1-p）=100×0.06=6，即np＞5，n（1-p）＞5，说明抽样分布趋于正态分布。若要求抽样估计的误差不超过3%，请计算出这种估计的置信度。

在采用重复抽样方法时

查标准正态分布函数表得F（Z）=F（1.26）=0.792 3，即这种估计的置信度为79.23%。