样本平均数的抽样分布定理有正态分布定理、中心极限定理和小样本分布定理。

（一）正态分布定理与抽样估计的置信度

正态分布定理：如果由n 个单位组成的随机样本来自一个平均数为、方差为的正态分布总体，则样本平均数服从于数学期望为、方差为的正态分布。

正态分布定理说明当总体服从正态分布时，按照随机原则从该总体中抽出一个容量为n的样本，无论该样本是大样本还是小样本，其样本平均数均服从正态分布，而且全部样本平均数的数学期望等于总体平均数，样本平均数的方差等于总体方差的，亦即抽样平均误差。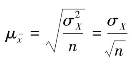

在实践中，为了应用方便，一般把正态随机变量变换为标准正态分布变量。这样就可以利用标准正态分布函数表查得抽样估计的概率度与相应概率的值，从而解决抽样估计的置信度问题。

由于从正态分布总体中随机抽样产生的样本平均数是服从于正态分布的一般随机变量，因此我们可以将其变换为标准正态分布随机变量。

在采用重复抽样方法时，变换公式为

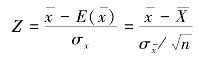
在采用不重复抽样方法时，变换公式为

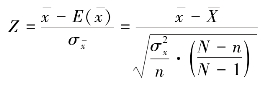
因为上述公式中的抽样标准误与抽样平均误差等价，所以在实际应用中，Z 的值可通过下式计算：

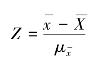
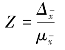
这样，就可以根据抽样估计的准确性要求和计算出的抽样平均误差来计算Z 值，然后从标准正态分布函数表中查出与之对应的概率值F（Z）。该概率值表明了用样本平均数估计总体平均数的置信度。这里，Z 是衡量抽样估计可靠概率的重要参数，被称为概率度。根据概率度、抽样极限误差、抽样平均误差与概率的关系，可以得出表6-5 中常用的概率，以便在实际中应用。

表6-5　常用的概率

【例6-5】　沿用【例6-3】　的资料，假设该居民区居民用电量服从正态分布，用抽样调查100 户居民该月户均用电量估计该居民区10 000 户居民的户均用电量时，若要求抽样误差不超过7 kW/h，请计算出这种估计的置信度。

在采用重复抽样方法时

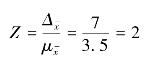(www.daowen.com)

查标准正态分布函数表得

由此可知，做出这种估计的置信度为95.45%。

在采用不重复抽样方法时

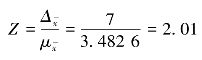
查标准正态分布函数表得

由此可知，这种估计的置信度为95.56%。

（二）中心极限定理与抽样估计的置信度

中心极限定理的通俗定义：对任意一个具有总体平均数为、方差为的总体，只要从该总体中随机抽取的样本容量n 无限增大（一般要求n＞30），则该样本平均数的分布趋近于其数学期望为、方差为的正态分布。

在抽样调查过程中，我们所要研究的现象总体各自都有不同的特征，有些总体服从正态分布，有些总体则服从其他形式的分布。对于服从正态分布的总体，有些可以事先知道，但更多的是事先不知道或根本无法知道的。中心极限定理的实用价值就在于，无论总体服从什么形式的分布，对于容量很大的样本来说，样本平均数的分布会接近于正态分布。因此，可以利用标准正态分布求得标准化随机变量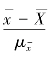落入一定区间的概率，进而推导出抽样估计的置信度。

（三）小样本分布定理与抽样估计的置信度

小样本分布定理：如果从平均数为、但方差未知的正态分布总体中随机抽取n 个单位组成样本，且n≤30，则样本统计量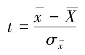服从自由度df=n-1 的t 分布。

其中，由于总体方差是未知的，因此是的估计值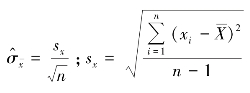，为样本标准差。

t 称为概率度，其本身没有计量单位。

t 分布的形状类似于正态分布，都是对称图形，但相对于正态分布偏平。当样本容量n不断增大时，t 分布趋近正态分布。事实上，当n＞30 时，二者就十分相近了。

t 分布的形态受自由度的影响。所谓自由度，就是我们能自由选择的数值的个数。当样本容量为n 时，df=n-1。

小样本分布定理说明，在研究实际问题时，总体方差往往是未知的，这时只能用样本方差代替总体方差，用样本标准差sx代替总体标准差σX。