社会经济统计中的平均指标有算术平均数、调和平均数、几何平均数、中位数和众数等形式。前三种平均数是根据总体全部单位标志值计算的，称为数值平均数；后两种平均数是根据与其所处位置有关的部分标志值计算的，称为位置平均数。在某些特定场合，位置平均数可以替代数值平均数来反映现象的一般水平。

（一）算术平均数

算术平均数是统计中最常用的一种平均指标。算术平均数的计算方法与大多数社会经济现象中个别现象与总体现象之间客观存在的数量关系一致。在统计中，算术平均数是总体标志总量与总体单位总数之比，即用总体中个体单位标志值的总和除以总体单位数。例如，工人劳动生产率是产品实物量与平均工人数之比，农作物平均产量是总产量与播种面积之比。其基本计算公式为

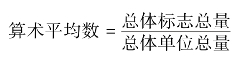
在计算算术平均数时，总体标志总量和总体单位总量必须属于同一总体，且所包含的内容在口径上应该严格一致，否则，计算的平均指标便失去了意义。这里要说明的是，算术平均数和强度相对数相似，都反映两个总量指标的对比关系，但强度相对数中用作对比的两个总量指标来自不同的总体，分子、分母不存在一一对应关系，即不存在各个标志值与各个单位相对应的问题；而平均指标是同一总体各单位标志值的平均，表现为总体内标志总量与总体单位数之比，分子分母存在一一对应关系，即一个单位必然对应一个标志值，分母量是分子量的承担者，所以计算平均指标时，分子、分母不能互换。

由于掌握的资料与计算复杂程度的不同，算术平均数的计算通常会采用简单算术平均数和加权算术平均数两种形式。

1.简单算术平均数

如果统计中没有直接掌握算术平均数基本计算公式中分子与分母项的资料，而只掌握了总体各单位的标志值（变量值），那么在计算平均数时，可将各单位的标志值相加得出标志总量，再用标志总量除以总体单位数。这种计算方法称为简单算术平均数法。

设x 代表算术平均数，xi（其中，i=1，2，3，…，n）表示各单位的标志值，则简单算术平均数的计算公式为

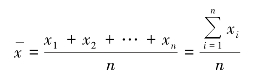
式中，n 代表总体单位数。

【例5-6】　某车间某小组5 名工人生产某种零件的日产量（件）分别为16、17、18、19、20，则这5 名工人生产该种零件的平均日产量为

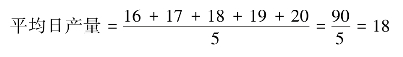
2.加权算术平均数

一个总体中的单位数往往有很多，要对某一方面的现象进行研究，需要首先将统计资料整理成变量分配数列，然后根据各组标志值及相应的单位数或频率计算算术平均数。这就是加权算术平均数的计算方法。加权算术平均数的计算分为以下两种。

（1）由单项数列计算加权算术平均数。在直接掌握各组标志值和各组单位数的条件下，计算加权算术平均数时，须先将各组的标志值乘以该组的单位数以求出每组的标志总量，再将各组的标志总量相加，求出总体标志总量，再用总体的标志总量除以总体单位数，得到加权算术平均数。

用xi代表各组标志值，fi（其中，i=1，2，3，…，n）代表各组单位数（权数），加权算术平均数的计算公式可表示为

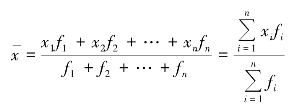
从上式可以看出，加权平均数的大小不仅受总体各单位标志值（xi）的影响，还受各组次数（fi）的影响。次数多的标志值对平均数影响大，次数少的标志值对平均数的影响小。标志值的次数对平均值的大小有权衡轻重的作用，所以把次数称为计算算术平均数的权数，把变量值乘以次数的过程叫加权。

【例5-7】　某车间有50 名工人，月产零件的分配数列资料如表5-3 所示。

表5-3　某车间工人月产零件的分配数列

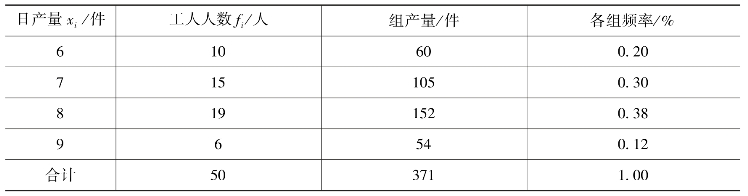
根据上述资料计算该车间工人的平均日产量，首先应计算全部工人的日总产量，然后将全部工人的日总产量和全部工人的人数相比。

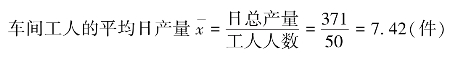
权数除用总体各组单位数即频数形式表示外，还可以用比重即频率形式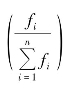表示。

用频率形式表示权数时，加权算术平均数的计算公式为

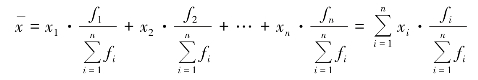
上式说明，权数权衡轻重的作用归根到底取决于各组单位数占总体单位数的比重。哪一组的单位数所占的比重大，哪一组标志值对平均数的影响就大。在【例5-7】　中，平均日产量为7.42 件，最接近于权数值为0.30 （15 人）的标志值（7 件）。

只有各个标志值的次数不相等时，次数作为权数才起作用。如果各组的单位数相等或各组单位数所占的比重相等，权数对各组的作用是一样的，那么次数作为权数就不起作用了，这时，加权算术平均数等于简单算术平均数。

【例5-8】　沿用【例5-7】　资料，假定每组都是20 人，其他资料不变。则

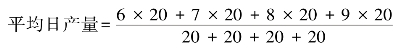
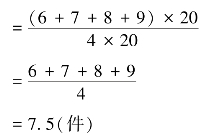
可见，简单算术平均数实际上是权数相等的加权算术平均数，是加权算术平均数的特例。

当f1= f2= … = fn= f 时

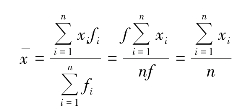
（2）由组距分配数列计算加权算术平均数。由组距分配数列计算加权算术平均数，是以各组的实际平均数乘以相应的权数来计算的。

实际工作中，在编制组距数列时，很少计算组平均数，通常会用各组的组中值近似地作为各组的代表值，同时假定各组内的标志值均匀分布或对称分布。然而，各组内的标志值不可能完全均匀或对称分配，因此组中值与组平均数之间必然会有一定误差，计算出来的加权算术平均数与实际平均数是有差别的。

【例5-9】　某班学生数学考试成绩资料及其平均成绩的计算如表5-4 所示。

表5-4　某班学生数学考试平均成绩

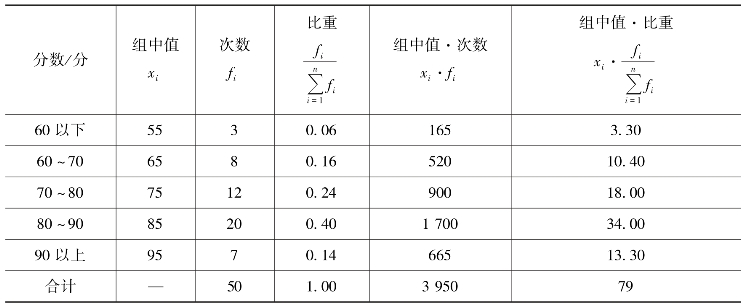
以次数为权数的平均成绩=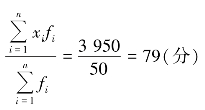

以比重为权数的平均成绩=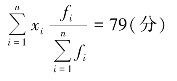

3.算术平均数的数学性质

（1）算术平均数与总体单位数的乘积等于各标志值的总和。

简单算术平均数

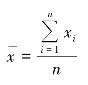
加权算术平均数

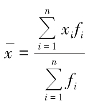
（2）各个变量值与算术平均数的离差之和等于零。

简单算术平均数

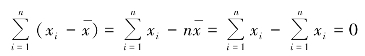
加权算术平均数

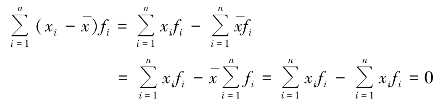
（3）各个变量值与算术平均数的离差平方和为最小值。

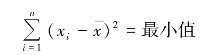
证明：设x0为任意值，，则有，以x0为中心的离差平方和为

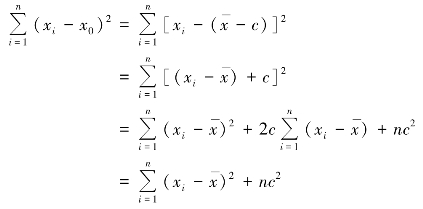
因为nc2≥0，所以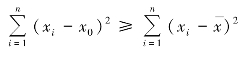，故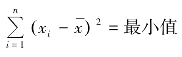。同理可证：。

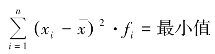（4）对各单位标志值加或减一个任意数A，则算术平均数要相应减去或增加该数A。

简单算术平均数

因为。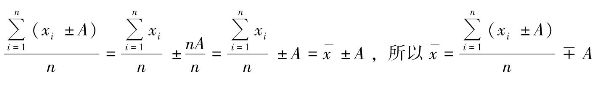

加权算术平均数

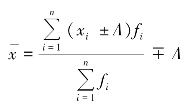
（5）对各单位标志值乘以或除以一个任意数A，则算术平均数要相应除以或乘以该数A。

首先，对各单位标志值乘以A。

简单算术平均数

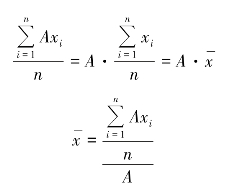
加权算术平均数

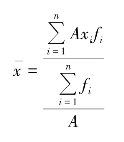
其次，对各单位标志值除以A。

简单算术平均数

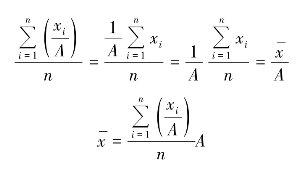
加权算术平均数

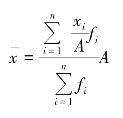
（二）调和平均数

调和平均数（H）是标志值倒数的算术平均数的倒数，又称倒数平均数。调和平均数有简单调和平均数和加权调和平均数两种形式。

1.简单调和平均数

简单调和平均数是在资料未分组的情况下，各标志值倒数的算术平均数的倒数。

设有n 个变量值x1，x2，x3，…，xn，那么各个变量值的倒数为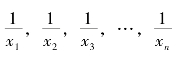，其倒数的算术平均数为

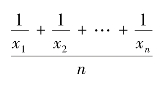
再求倒数的算术平均数的倒数，即为简单调和平均数

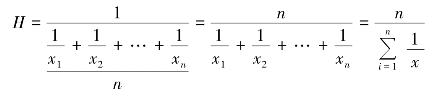
【例5-10】　某市场上有三种苹果，富士每千克5 元，秦冠每千克4 元，红星每千克3.5元，若各买1 千克，平均每千克多少元？

这个问题的实质是计算简单算术平均数，即

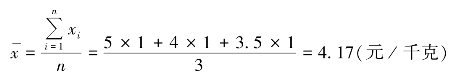
【例5-11】　沿用【例5-10】　的资料，若三种苹果各买1 元，平均每千克多少元？

这个问题的实质是计算简单调和平均数，即

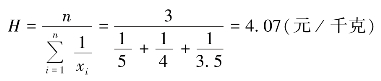
上例表明，当要研究的问题对平均数要求不同时，计算平均数的方法也不同，其计算结果及实质含义也有所区别。采用简单算术平均数还是简单调和平均数主要取决于平均的条件。简单调和平均数是在各变量对平均数起同等作用的条件下应用的。如【例5-11】，在每种苹果各买1 元的条件下，平均的对象是分子单位数，即金额相等，而每种价格对平均价格的影响是不同的，由于价格最低的红星苹果买得最多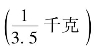，以致平均价格相对较低。

2.加权调和平均数

（1）加权调和平均数的一般公式。加权调和平均数是在次数分配数列的条件下，计算各变量值倒数的加权算术平均数的倒数。在实际统计工作中，常会遇到只有各组标志总量而缺少总体单位数的变量数列资料的情况，此时无法直接按加权算术平均数的公式计算平均数，需要运用加权调和平均数。加权调和平均数的计算公式为

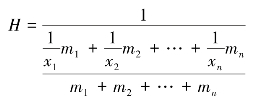
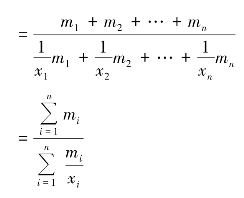
式中，m 代表权数。

（2）由平均数作为变量值计算加权调和平均数。

【例5-12】　三个市场某种商品本月平均价格及采购资料如表5-5 所示，试计算三个市场该种商品的平均采购价格。

表5-5　三个市场某种商品平均价格及采购资料

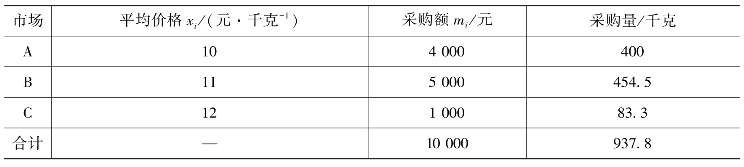
已知平均价格和采购额时，要以采购额为权数，用加权调和平均数计算三个市场某商品平均采购价格。

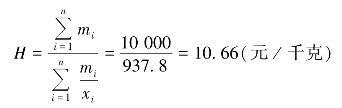
上例中，若已知平均价格和采购量，则应以采购量为权数，用加权算术平均法计算。

对于同一资料，应用加权算术平均法和加权调和平均法计算结果是相同的，实际意义也相同。即mi=xifi时，有

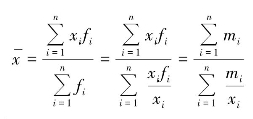
因此，加权调和平均数是加权算术平均数的变形，两者都是总体标志总量与总体单位总量之比。

（3）由相对数作为标志值计算加权调和平均数。

【例5-13】　某公司下属三个子公司计划完成情况的组距数列资料如表5-6 所示，计算其平均计划完成程度。

表5-6　三个子公司平均计划完成程度计算表

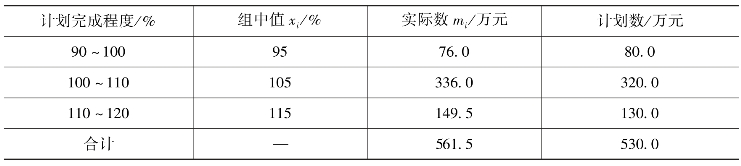
注：计划数=实际数/组中值=mi/xi。

平均计划完成程度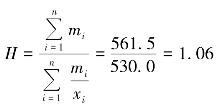

上例中，若已知计划完成程度和计划数，要计算平均计划完成程度，应以计划数为权数，用加权算术平均数来计算。

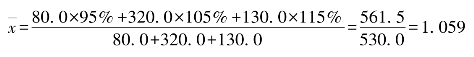
由以上两道例题可知，由平均数或相对数计算平均数时，应根据已知的不同资料，采用不同权数进行计算。若已知权数是相对数或平均数的分子项资料时，应采用调和平均数计算；若已知的权数是相对数或平均数的分母项资料时，应采用算术平均数计算。

（三）几何平均数

几何平均数是n 个单位标志值的连乘积的n 次方根，只有一些特殊的比率才具有这一特征。几何平均数适用于计算标志值的连乘积等于总比率或总速度的社会经济现象的平均比率或平均速度。几何平均数分为简单几何平均数和加权几何平均数。

1.简单几何平均数

简单几何平均数是n 个变量连乘积的n 次方根。适用于资料未分组的情况，其计算公式为(www.daowen.com)

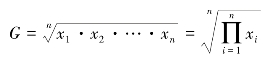
式中，G 代表几何平均数；x 代表各标志值；n 为标志值的个数。

【例5-14】　某企业采用分步法生产某产品，该产品的生产依次经过铸造、加工、装配、电镀这四个连续作业的车间，各工序产品合格率分别为95%、90%、91%、85%，求四个车间的平均产品合格率。

这里不能用算术平均数或调和平均数计算，因为各道工序的合格率总和并不等于该产品的总合格率。第二车间的合格率是在第一车间制品全部合格的基础上计算的，第三车间合格率又在第一车间、第二车间制品全部合格的基础上计算。全厂产品总合格率等于各车间合格率的连乘积，应采用简单几何平均数计算产品的平均合格率。即

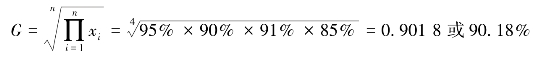
在变量数值较多的情况下，计算几何平均数需要开多次方，为了方便计算，通常利用对数计算。将几何平均数公式两边各取对数可得

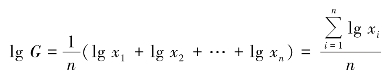
通过上式求出几何平均数的对数后，再由对数找出真数，即为几何平均数。

2.加权几何平均数

当各个变量值出现的次数不相同时，应采用加权几何平均数，其计算公式为

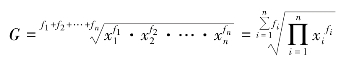
式中，f 代表各标志值的次数（或权数），为次数（或权数）的总和。

对上述公式两边取对数，则有

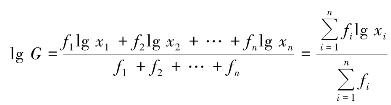
【例5-15】　某投资银行某笔投资的年利率按复利计算，投资期为10 年。10 年的利率分别是：第一年至第二年为5%，第三年至第五年为8%，第六年至第八年为10%，第九年至第十年为12%，求平均年利率。

本例中，计算平均年利率须先将各年利率加100%换算为各年本利率，然后按加权几何平均数计算平均年本利率，再减100%计算出平均年利率，计算过程如表5-7 所示。

表5-7　平均年利率计算

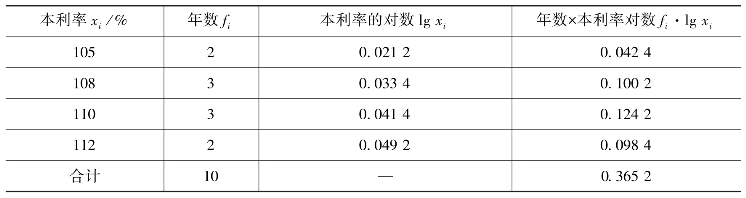
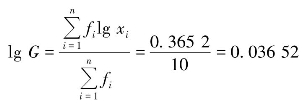，可得G =1.087 7 或108.77% ，则平均年利率=108.77%-100% =8.77%。

从上述计算过程可以看出，如果数列中有一个标志值为零，就不能计算几何平均数；如果数列中有负数，计算出的几何平均数就会为虚数。

从数量关系上来看，用同一资料计算三种平均数的结果是几何平均数大于调和平均数而小于算术平均数，当所有变量值都相同时，三种平均数相等。三者关系如下：

根据以上不等式关系可以得出：当该用算术平均数计算时误用调和平均法，则所得结果偏小；该用几何平均法计算时误用算术平均法，则结果偏大。

（四）中位数

算术平均数、调和平均数和几何平均数都是根据总体中的全部标志值计算的，一般称为数值平均数。数值平均数易受极大值、极小值的影响，会减弱平均指标在总体中的代表性。众数和中位数是另一种类型的平均指标，是根据其在总体中所处的位置或地位确定的，不受数列中极端值的影响，一般称为位置平均数。

1.中位数的定义

中位数是指把总体单位的某一数量标志的各个标志值按其大小顺序排列，居于中间位置的标志值就是中位数，一般用me表示。中位数不受标志中极端数值的影响，可以从另一个侧面反映次数分配的集中趋势。

从中位数的定义可以看出，数列中有一半单位的标志值小于中位数，另一半单位的标志值大于中位数。在某些研究中，我们可以用中位数表示现象的一般水平，它对总体分析具有特殊意义。例如，在研究社会居民收入水平时，居民收入中位数比平均收入更能代表居民的收入水平。又如，据1953 年、1964 年、1982 年、1990 年人口普查资料显示，我国人口年龄中位数分别为22.7 岁、20.2 岁、22.9 岁、25.3 岁，这些数字反映了我国人口年龄的结构水平，据此可以判断当时我国人口类型属于中年型。

2.中位数的确定

根据掌握的资料，中位数的确定有以下三种情况。

（1）由未分组资料确定中位数。

在标志值未分组的情况下，可以先将各单位的标志值按大小顺序排列，然后用（n为标志值的个数）来确定中位数的位置，该位置上的标志值即为中位数。

如果研究的总体单位数是奇数，则居于中间位置的标志值就是中位数。

【例5-16】　一学习小组有5 名学生，其英语课成绩按顺序排列为56、62、67、75、81。那么，中位数就是第三项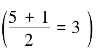上的标志值，即67 分。

如果研究的总体单位数是偶数，那么居于中间位置两边标志值的算术平均数就是中位数。

【例5-17】　沿用【例5-16】　资料，假如该学习小组有6 名同学，第6 名同学的英语成绩为85 分。则中位数位置为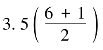，中位数为第三项和第四项的算术平均数，即。

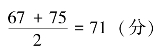（2）由单项数列确定中位数。

首先，根据累计次数确定中位数位置。目的是保证中位数所在位置前后两部分次数相等。位置公式为

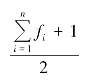
其次，用累计次数的方法找出中位数所在组。既可以由标志值最小组向最大组逐组累计次数（即向上累计），也可以由标志值最大组向最小组累计次数（即向下累计）。

最后，找出中位数所在组，该组的标志值就是中位数。

【例5-18】　某地区居民家庭收入情况如表5-8 所示。

表5-8　某地区居民家庭收入情况

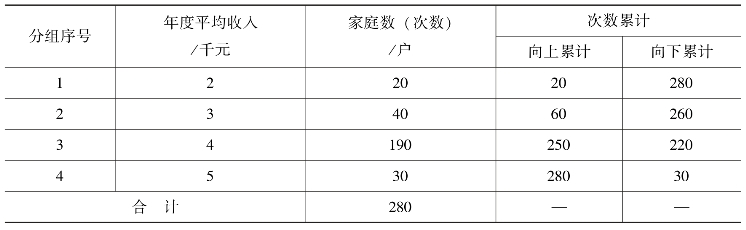
首先，确定中位数位置。

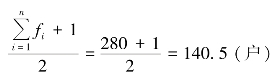
说明中位数位置在140 户和141 户之间。

其次，根据累计次数可知，第140 户和第141 户都在第三组，其标志值相同。

最后，中位数在第三组，且标志值都是4 000，即中位数为4 000 元。

（3）由组距数列确定中位数。

首先，计算各组累计次数，并按公式确定中位数所在组的位置。在未分组资料和单项数列中，用和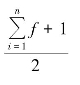来确定中位数的位置，是由于位置（即间隔）比点数少1，加上1 点除以2 后所得的点数正好是中间位置，不加1 点就会相差半个位置。而在组距数列中，是以距离个数来确定位置的，因此直接用确定中位数位置。

其次，确定中位数所在组。

最后，计算中位数的近似值。由组距数列计算中位数是假定各组的次数在各组内是均匀分布的。因此，可用中位数所在组次数与其以上各组或以下各组累计次数之间的关系确定一个比例，用插入法计算中位数的近似值。其具体过程有以下两种形式。

第一种形式，先算出中位数所在位置对应的次数与中位数所在组以下各组累计次数的差额，再计算该差额在中位数所在组的次数中所占比例，之后用组距乘以该比例折算组距单位数（即组距×比例），则中位数的具体数值为中位数所在组下限加组距单位数。这种计算方法是用中位数所对应的次数与中位数所在组以下累计次数确定比例来计算的，其计算公式称为下限公式，即

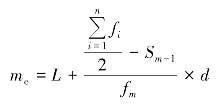
式中，me代表中位数；L 代表中位数所在组下限；fm代表中位数所在组次数；代表总次数；Sm-1代表中位数所在组以下各组的累计次数；d 代表中位数所在组的组距。

第二种形式，先算出中位数所在位置对应的次数与中位数所在组以上各组累计次数的差额，再计算该差额在中位数所在组的次数中所占比例，之后用组距乘以该比例折算组距单位数，则中位数的具体数值为中位数所在组上限减组距单位数。这种计算方法是用中位数所对应的次数与中位数所在组以上累计次数确定比例来计算的，其计算公式称为上限公式，即

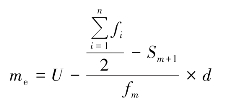
式中，U 代表中位数所在组的上限；Sm+1代表中位数所在组向上各组的累计次数。

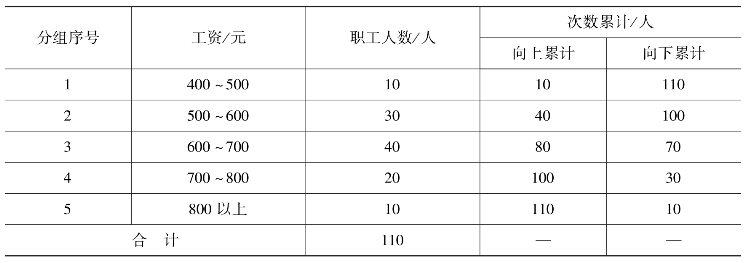
【例5-19】　某公司某月职工工资情况如表5-9 所示。

表5-9　某公司某月职工工资

首先，计算中位数位置。

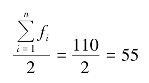
说明中位数在第55 人的位置上。

其次，确定中位数所在组。无论是由向上累计还是向下累计，中位数都在第三组（600 ～700 元）。

最后，确定中位数。第三组下限为600 元，上限为700 元，组距100，组内次数（即中位数所在组次数）为40 人。下面分别采用下限公式和上限公式计算中位数的近似值。

将上述资料代入下限计算公式，即

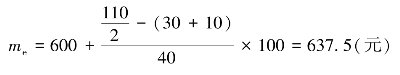
将上述资料代入上限计算公式，即

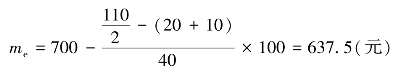
从计算结果来看，两种方法计算的中位数是相同的。

中位数作为一种位置平均数，不受极端值影响，以其作为标志值数列的平均水平缺乏代表性。但如果数列中存在极大或极小值，中位数就能较好地反映现象的一般水平。在社会经济统计中，对于等级、顺序、名次这些不能用数量表示的标志，比较适合用中位数代表其一般水平。

（五）众数

1.众数的定义

众数是现象总体中出现次数最多的标志值，常用m0表示。众数也是一种位置平均数，可以说明总体中某个标志值分布的集中趋势，反映现象的一般水平。例如，某单位5 名职工工资分别为600 元、700 元、700 元、700 元、800 元，其中700 元出现次数最多，即为众数，可以用其代表5 名职工收入的一般水平。

又如，服装生产企业为了满足消费者的需要，需要了解需求量最大的服装的规格、型号，为安排生产和销售计划提供依据。再如，为了掌握市场上某种商品的价格水平，可不必全面登记该商品的全部成交量与成交额，只需获知该市场当日最普遍的成交价格即可。

2.众数的确定

根据掌握的资料，众数的确定有以下两种情况。

（1）由未分组、单项资料确定众数。

在未分组资料或单项数列中，众数不需要计算，而是通过直接观察确定，以次数出现最多的标志值为众数。

【例5-20】　某地区家庭人口数分组情况如表5-10 所示。

表5-10　某地区家庭人口数分组情况

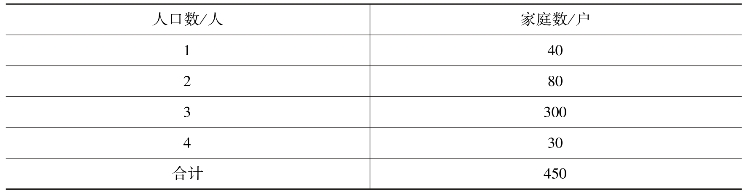
众数就是每户3 人，因为这个变量值所在组的次数（300 户）最多。

（2）由组距数列确定众数。

由组距数列确定众数，应首先确定次数量最多的一组为众数所在组，再用公式近似计算众数。类似于中位数的确定，其计算公式有以下两种。

下限公式为

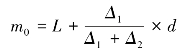
式中，m0代表众数；L 代表众数所在组的下限；Δ1代表众数所在组次数与前一组次数之差；Δ2代表众数所在组次数与后一组次数之差；d 代表众数所在组的组距。

上限公式为

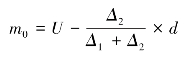
式中，U 代表众数所在组的上限，其余符号不变。

【例5-21】　沿用【例5-19】　中的数据，“600 ～700 元”组的次数最多，有40 人，因此该组就是众数组。

用下限公式确定众数为

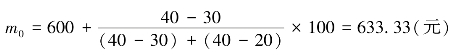
用上限公式计算众数为

众数不受各变量值的影响，因此，用它作为变量值的代表值也有不足之处。但当数列中存在差异变量值时，它比算术平均数更能准确地代表现象的一般水平。由于众数属于次数最多而又高度集中的数值，因此它仅适用于分布的次数较高且有明显集中趋势的总体，若变量数列呈现均匀分布，就无众数。若有些变量数列的次数分布表现为有多个分散的集中趋势，这时，可将各组次数按顺序两两合并，求出一个明显的集中趋势来求众数。

（六）算术平均数、中位数和众数的关系

算术平均数、中位数和众数之间的关系取决于总体内的次数分配状况。当总体内次数呈正态分布时，算术平均数、中位数、众数表现为同一数值。当次数分配不对称时，众数、中位数与算术平均数之间有差别，这种差别与非对称程度有关。非对称的程度越大，它们之间差别越大。若存在非正常的极端变量值，变量分配会产生偏斜。极端变量值对三种平均数的影响不同：算术平均数受所有变量值的影响，极端变量值对其影响最大；中位数只受极端变量值位置的影响，不受数值影响；众数决定于分配次数最多的变量值，不受极端值的影响。

大量实际经验数据表明，在分配数列分布适度偏斜的情况下，三个数的近似关系是：算术平均数与众数的距离约等于算术平均数与中位数距离的三倍。在偏态分布中，若出现大的极端变量，即次数分布是右偏，算术平均数大于中位数，而中位数大于众数，即，并有关系；当次数分布左偏时，算术平均数小于中位数，而中位数又小于众数，并有关系，注意这里的是负数。

根据三个平均数的近似等式还可推出以下两个近似等式。

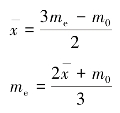
利用这些关系式，可以根据已知的两个平均指标来估计第三个平均指标。

（七）应用平均指标的原则

1.平均指标应用于同质总体

用平均指标作为总体某一数量标志的代表值，要注意总体各单位的同质性。所谓同质性，就是总体各单位在被平均的标志上具有同类性，即平均数不是一种混杂的平均数。例如，要研究居民的平均收入，就不能把农民的收入和城镇职工的收入混在一起计算；要研究农作物的平均产量，就不能把粮食作物和经济作物混在一起计算。将不同性质的总体单位混在一起计算平均数，不但不能反映社会经济现象的本质特征，还会掩盖实际情况，歪曲事实真相。因此，只有在同质总体内计算平均数，才能反映现象总体的一般水平。

2.用组平均数补充说明总平均数

根据同质总体计算的总平均数，虽可以反映总体各单位标志值的一般水平，但会掩盖其他方面的差别，特别是结构上的差别。因此，需要通过分组来表明总体内部各部分的比重或比例关系，通过计算组平均数补充说明总平均数，使平均指标能够正确分析与说明事物的发展变化。

【例5-22】　甲、乙两个自然村粮食生产情况如表5-11 所示。

表5-11　甲、乙两个自然村粮食生产情况

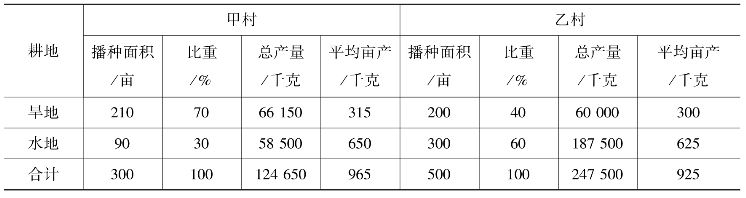
从表5-11 中总平均数来看，甲村粮食总平均亩产为415.5 千克，乙村总平均亩产为495 千克，乙村大大超过甲村。若从组平均数来看，甲村旱地平均亩产315 千克，乙村300千克；甲村水地平均亩产650 千克，乙村625 千克，甲村均高于乙村。造成这种差别的原因，是甲村地理条件差，水地播种面积占总面积的30%；而乙村地理条件好，水地面积占总面积60%，即甲、乙两村播种面积的构成比重不同。总平均数把旱地生产水平和水地生产水平的差别，以及两村在两种不同生产水平的播种面积结构上的差别扯平了。因此，应该用组平均数补充说明总平均数，以便正确评价甲、乙两村的生产成果。

3.用分配数列补充说明平均指标

平均指标把总体各单位的差别抽象化，掩盖了总体各单位的差异及其分配状况。当总体单位标志值较为集中时，平均指标代表性就大；反之，代表性就小。为了全面分析问题，不能只看现象的平均水平，还必须了解平均水平掩盖的具体数值的分配状况，即用分配数补充说明平均指标。例如，某地区平均计划完成程度为103%，总体上看，该地区超额完成计划，但就分配数列来说，有10 个企业未完成计划，这样反映的问题就更加具体了。

4.平均分析与个别分析相结合

平均指标反映社会经济现象在一定时间、地点条件下所达到的一般水平。用平均指标分析时，必须注意其具体情况、具体条件，把平均分析与个别分析结合起来。平均分析与个别分析结合的内容有很多，主要包括：具体分析对比两个平均指标的可比性；平均指标和个别典型事例结合，补充平均指标的不足，丰富平均指标对社会现象的认识。