为了正确地编制组距数列，需要明确以下几个概念。

（一）全距

全距是指在被整理的总体中，最大标志值与最小标志值之间的距离，即全距=最大标志值-最小标志值，其表达式为R=Xmax-Xmin。

（二）组限、组距与组数

在组距式变量数列中，各组的变动范围是以组限来表示的。组限规定每组距离的数值，即每组的起点值和终点值的数值。每组的起点值被称为下限，终点值被称为上限。组距是上限与下限的差额，即组距=上限-下限。组数是按照某个标志将总体划分为若干个组成部分的数量。例如表4-6 中，最小的一组是50 ～60，则50 为下限，60 为上限，其余组依次类推。其中，最小组的组距=上限-下限=60-50=10。

组距的大小和组数的多少是相互联系的。总体中，在各单位的标志值变动范围一定的情况下，若扩大组距，则组数减少；若缩小组距，则组数增加。统计中，在确定组距与组数时，需保证使所确定的组距和组数能将总体中性质相同的单位分在同一组，而将性质不同的单位分在不同的组。

对于组距和组数，先确定什么，后确定什么，不能生搬硬套，通常是先确定组距。确定组距应遵循以下四个原则：

（1）根据统计研究的目的和所研究现象的特点确定组距。

（2）要能显示出总体分布的特点。

（3）要充分考虑原始材料的整体分布情况。

（4）要考虑到组距的同质性，严格、正确地把握和区别事物的质量和数量界限。

（三）组限的表示方法

连续型变量数列与离散型变量数列组限的表示方法有所不同。(www.daowen.com)

按连续型变量分组时，应采取连续组限，又称同限分组。例如表4-6 中相邻两组的上、下限相同，第一组的上限为60，第二组的下限也是60；第二组的上限为70，第三组的下限也是70 等。因此，连续型变量只适宜编制组距数列，不宜编制单项数列。若连续型变量的某一个数值正好等于组限，则一般将这个标志值划在作为下限的那一组。

离散型变量分组的相邻组的组限应断开，又称异限分组。例如，表4-7 按职工人数分组中第一组的上限是100，第二组的下限为101，以后各组皆如此，即为异限分组。

（四）组中值

组中值是指该组中点位置的数值。组距式分组掩盖了同一组内各变量的真实分布情况。例如，表4-6 中第三组70 ～80 中有16 人，但从这个分组表中无法得知这16 人的具体分数。统计上，一般假定同一组内的各变量值是均匀分布的。在这个假定下，可以用平均的方法计算出组中值，来作为该组的代表值。组中值按如下公式计算：

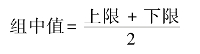
例如，表4-6 中第三组和第一组的组中值分别为

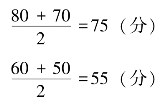
假定第三组的16 人都得75 分，第一组的2 人都得55 分。

（五）开口组及其组中值计算

在分组中，第一组和最末一组往往会出现“××以下”“××以上”等字样，这种组叫开口组。开口组组中值的计算在缺下限开口组和缺上限开口组有所不同。

例如，将粮食按产量分为以下组：200 千克以下；200 ～300 千克；300 ～400 千克；400 ～500 千克；500 千克以上。则