1.信息机制各指标的相关性检验

依据上一章表3-8信息机制各指标的数据，以SPSS17.0软件为工具，对信息机制各指标的数据进行相关性分析。为避免分析结果受测量量纲的影响，先要对数据进行标准化处理。^[1]对数据的标准化处理我们选择了Z标准化方法，计算公式如下：

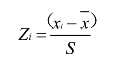
“其中xi是该变量的样本值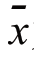，为样本平均值，S是样本标准差。Z标准得分表示一个变量值与该变量的平均值之差是标准差的倍数”。^[2]

为了研究的便利，对表3-8中21家样本社会智库信息机制的各指标数据进行命名。用X1代表间接信息源（XXY），X2代表知名人士（ZMRS），X3代表政府官员（ZFGY），X4代表友情链接（YQLJ），X5代表合作单位（HZDW），X6代表智库负责人影响力（FZRYXL），X7代表资料存储机构（ZLCQJG），X8代表时间（SJ）。

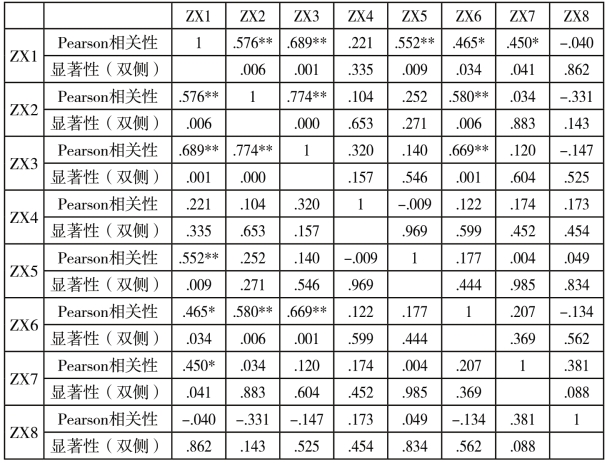
相关性检验及相关系数矩阵如表4-1所示（分析数据来源于表3-8标准化后的数据）。

表4-1　信息机制各指标的相关系数矩阵

**表示显著性水平P＜0.01。*表示显著性水平P＜0.05

表4-1显示：（1）智库成立时间的长短与其他指标间不存在显著正相关（P＞0.05）。如中国与全球化智库、中国国际经济交流中心，成立时间虽短，但无论是影响力还是研究成果的产出以及在社会智库排名方面均高于成立时间较长的世界与中国研究所和北京大军智库经济咨询有限公司。（2）间接信息源与智库负责人的影响力、社会智库内的政府官员、知名人士间存有明显的正相关性（负责人影响力相关系数r=0.465，P＜0.05，政府官员和知名人士的相关系数r=0.689和0.576，P＜0.01），表明当前社会智库信息的来源主要还是依赖社会智库负责人、政府官员、知名人士的人脉关系。如中国国际经济交流中心和“中改院”的负责人曾经的行政级别均在副部级及其以上，一定程度上便利了信息与数据的获取。（3）合作单位虽然也是智库信息的来源，但这一变量仅与间接信息源呈正相关性（相关系数r=0.552，P＜0.01），与政府官员和知名人士间相关性不显著，这可能缘于合作单位这一指标的数据差异过大，如自然之友的合作伙伴有83家，而“中改院”则是25家，综合开发研究院为6家。但这些知名社会智库内部拥有较多行政级别高的官员和众多知名人士，在研究信息与数据的获取方面更具优势，合作单位在信息获取方面甚至要依赖他们。（4）资料存储机构除与间接信息源存有正相关外（相关系数r=0.450，p＜0.05），与其他变量不存在相关性，这可能受各样本社会智库间资料存储机构的差异过大影响。

2.信息获取能力的回归分析

为进一步探索表3-8社会智库信息机制各指标间的关系，探寻各样本社会智库的信息获取能力，本部分选择了多元线性回归分析的方法，公式如下：

上式中Y是因变量。β0、β1、β2……βp是p+1个未知参数，β0称为回归常数，β0、β1、β2……βp称为回归系数。x1、x2、……xP是P个可供测量与控制的自变量，本部分主要指政府官员数量、知名人士、负责人影响力、合作单位以及社会智库内部的资料存储机构。ε是随机误差，其满足条件是ε-N（0，σ2）。^[3]

为更好地验证各指标数据对因变量间接信息源的影响，依据表3-8的数据（标准化处理后的数据）选择了逐步回归的方法。逐步回归的基本思想是通过筛选、挑选偏回归平方和贡献因子来建立回归方程，在决定是否引入一个新的影响因素时，用方差进行显著性检验，如果判定这个影响因素通过显著检验，则将该因素归入回归方程中，否则不进入。^[4]其优点在于降低自变量间的干扰，提高回归模型的准确度。^[5]分析步骤及其结果如下：

（1）变量筛选过程。表4-2输入和移去的变量表格给出了信息机制各指标的逐步回归过程；①引入了政府官员变量，建立了模型1；②引入了合作单位，建立了模型2；③引入资料存储机构变量，建立了模型3。而知名人士和负责人影响力则被排除出了回归过程。

表4-2　信息机制回归分析输入／移去的变量a

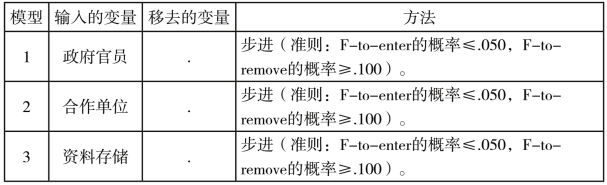
a.因变量：间接信息源(www.daowen.com)

（2）模型信息摘要。表4-3模型汇总表格给出了关于模型的拟合情况，可以看出，模型3的调整R2为0.751，大于模型1和模型2，“说明模型可解释的变异占总变异的比例越来越大，引入方程的自变量有一定效果，拟合度也较好，自变量对因变量具有较强解释力”。^[6]

表4-3　信息机制回归分析的模型汇总

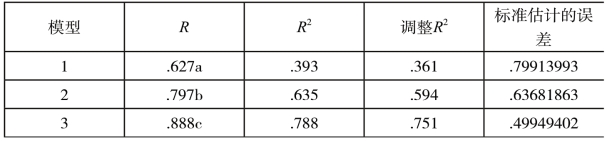
a.预测变量：（常量），Zscore：政府官员。b.预测变量：（常量），Zscore：政府官员，Zscore：合作单位。c.预测变量：（常量），Zscore：政府官员，Zscore：合作单位，Zscore：资料存储机构。d.因变量：间接信息源

（3）方差分析表。表4-4Anova表格的模型3给出了回归拟合过程中的方差分析结果，F检验统计量为21.054，对应的P值接近0。说明该模型通过了F检验，解释变量和被解释变量间的线性关系是显著的，可构建多元线性回归方程。

表4-4　信息机制回归分析的Anova表

a.预测变量：（常量），Zscore：政府官员。b.预测变量：（常量），Zscore：政府官员，Zscore：合作单位。c.预测变量：（常量），Zscore：政府官员，Zscore：合作单位，Zscore：资料存储机构。d.因变量：Zscore：间接信息源

（4）回归系数估计。表4-5回归系数表格给出了最终模型的回归系数估计值，根据模型3可建立标准化的线性回归方程，如下式：

在多元回归分析中，要考察哪些因素是影响Y的主要因素和次要因素，通常要用标准化系数。自变量在任或退休政府官员、合作单位、资料存储机构的标准化回归系数分别为0.526、0.499和0.393。说明在各样本社会智库信息获取能力方面，政府官员的作用要大于合作单位和资料存储机构，合作单位次之，再者是资料存储机构。t检验中，政府官员、合作单位和资料存储的显著性P＜0.01，均具有显著意义。为避免回归过程中多重共线性问题存在，对模型进行了共线性检验。多重共线性是指解释变量之间存在线性相关关系的现象。^[7]自变量的高度重合会对回归方程带来影响。可用方差膨胀因子（VIF）检测共线性的存在。^[8]当0＜VIF＜10，不存在多重共线性；当10≤VIF＜100，存在较强的多重共线性。经过线性回归过程中的共线性检验，本部分三个自变量的膨胀因子（VIF）分别为1.026、1.016和1.010，说明模型3中三个自变量间不存在共线性。

表4-5　信息机制回归分析的系数

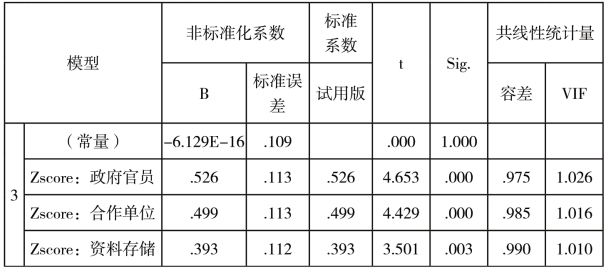
a.因变量：间接信息源

（5）已排除变量的统计信息表。表4-6在模型1中将知名人士、合作单位、资料存储机构、负责人影响力排除，仅有政府官员被纳入了方程。但合作单位和资料存储机构的t检验的显著性概率P＜0.05。在模型2中合作单位被纳入了回归方程，在模型3中资料存储机构也被纳入了回归方程，知名人士数量和负责人影响力被最终排除出了回归方程，两者的t检验显著性概率P＞0.05，难以被纳入模型。

表4-6　信息机制回归分析中已排除的变量d

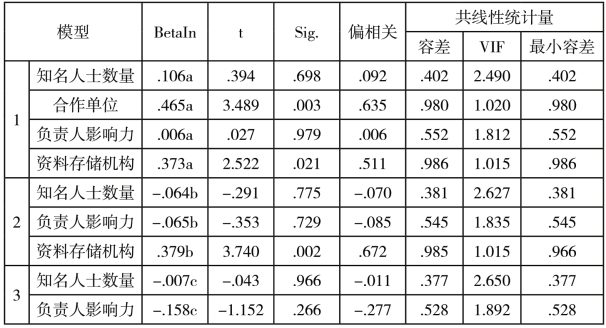
a.模型中的预测变量：（常量），政府官员。b.模型中的预测变量：（常量），政府官员，合作单位。c.模型中的预测变量：（常量），政府官员，合作单位，资料存储机构。d.因变量：间接信息源

上述数据分析表明，社会智库内退休或在任政府官员对社会智库信息的获取具有重要作用，本项研究假设H2a：通过了验证。知名人士虽与社会智库信息渠道在相关系数矩阵中存有明显的正相关，但在回归过程中不显著，这可能是受到各样本数据的影响，也可能受到回归过程中其他变量的影响。H1a：未通过验证。合作单位与各样本社会智库间接信息源显著性较强，通过了回归方程检验，因此，H3a：通过验证。