用AHP分析问题大体经过以下五步：

（1）建立层次结构模型。

（2）构造判断矩阵。

（3）层次单排序。

（4）层次总排序。

（5）一致性检验。

1.建立层次结构模型

AHP在分析复杂问题时，首先从系统的层次特性出发，用一个层次结构模型，描述问题所涉及的因素及其相互间的关系。层次结构模型如图27-11所示。

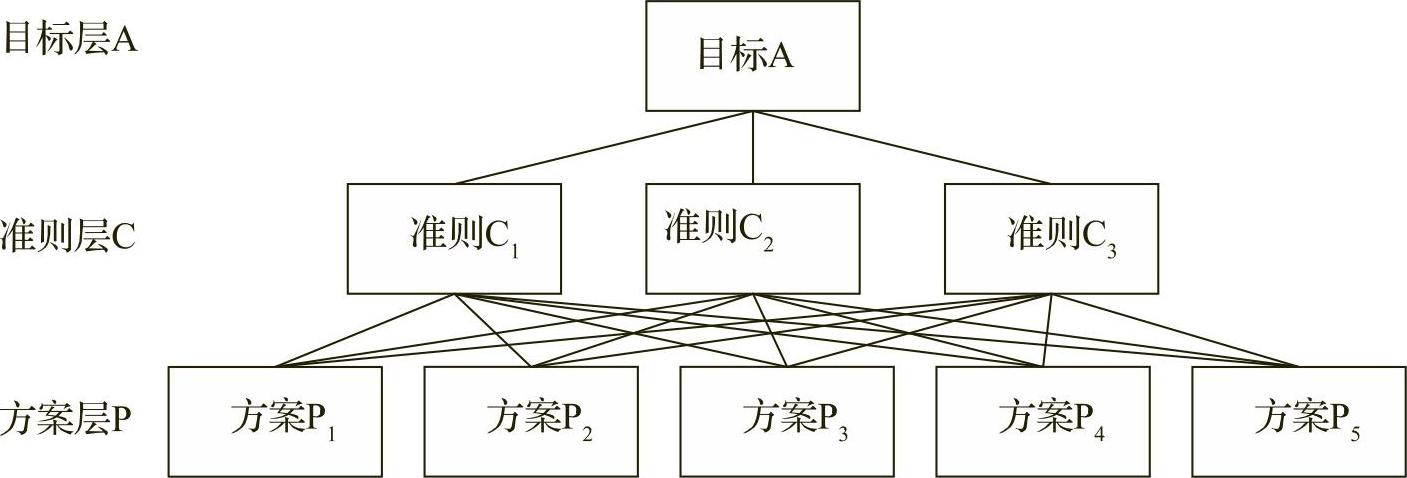
图27-11 层次结构模型

最高层：表示解决问题的目的。

中间层：表示采用某种措施和政策来实现预定目标所涉及的中间环节，一般又分为策略层、约束层、准则层等。

最底层：表示解决系统问题的各种备选方案、政策，措施等。

在构造实际问题的层次结构模型时，首先要分解得到构成要素，按要素的特点进行归纳，排为若干层次。对于有关联的要素，用作用线连接起来，即可建立层次结构模型。也可以采用目标手段分析方法，来寻求达到目标应采取的手段以及评价方案的准则和指标，由此建立层次结构模型。在某些复杂的社会经济问题的层次结构中，还会存在从下层到上层的反向作用，形成具有反馈的层次结构。如果上层的每一个要素与下层的所有要素都存在联系，就称为完全相关结构；如果上层要素仅与下层的部分要素相关，则称为不完全相关结构。

2.构造判断矩阵

判断矩阵是将层次结构模型中同一层次的要素相对于上层的某个因素作成对比较而形成的矩阵。以图27-11所示的层次结构为例，方案层的备选方案B₁，B₂，…，B_n相对目标层的准则A_k作成对比较，可构成下面的判断矩阵A见表27-2。

表27-2 判断矩阵A

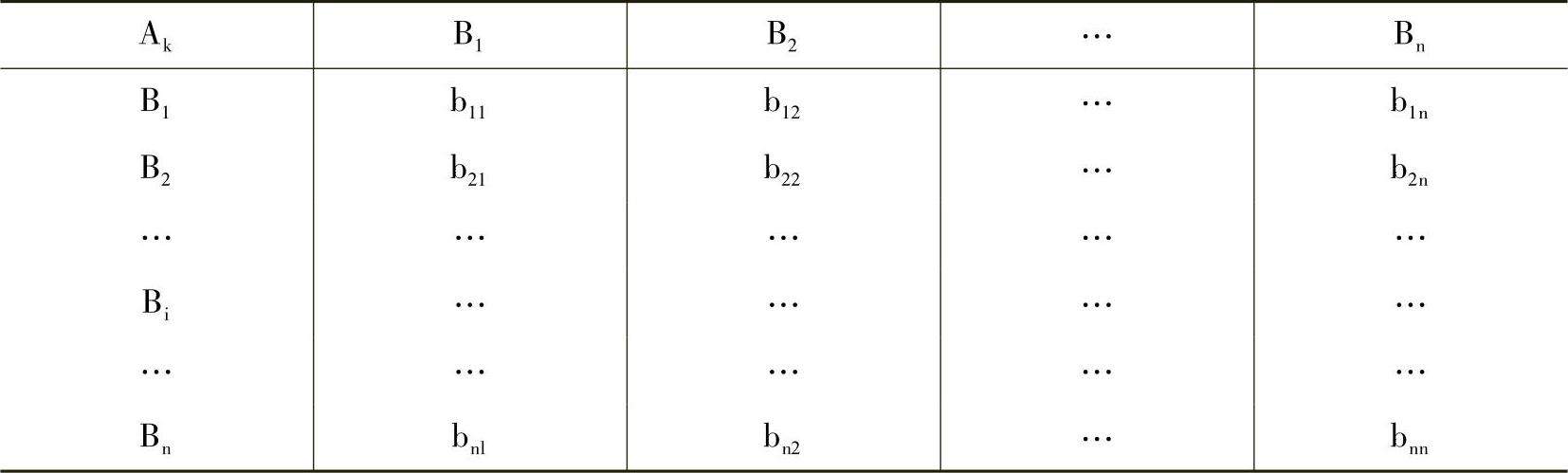
其中，b_ij是以A_k为准则B_i对B_j的相对重要性的数值表示。通常使用1～9标度法来确定b_ij的取值，见表27-3。

表27-3 1～9标度法

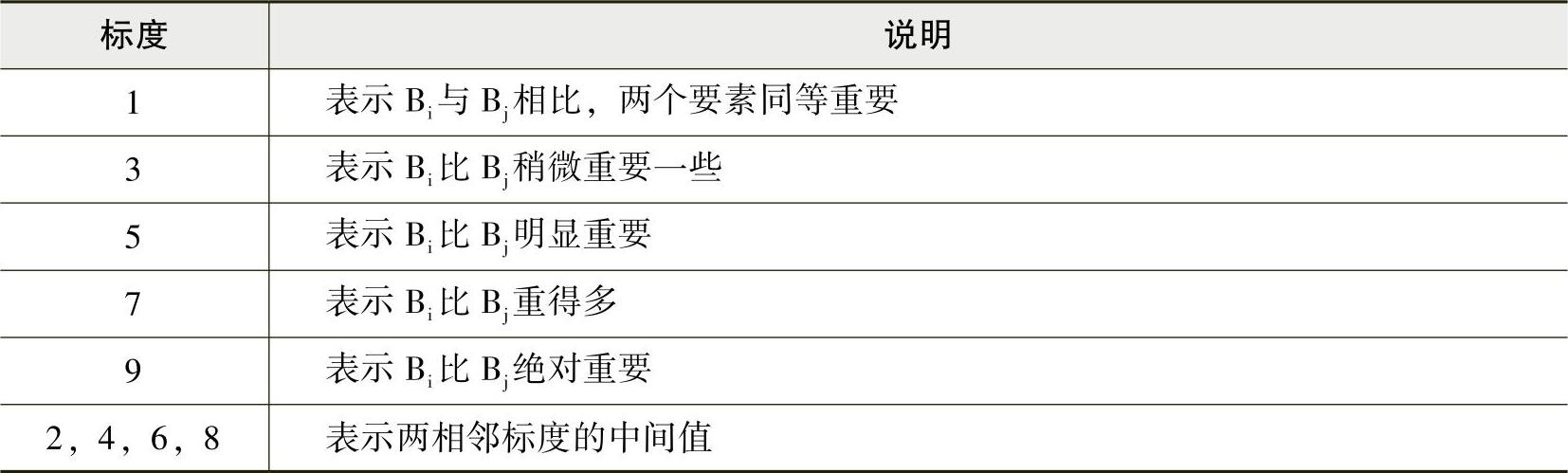
通过比较得到的判断矩阵A=[b_ij]_n×n具有以下特点：

①b_ij＞0

②b_ii=1

③b_ij=1/b_ji（i，j=1，2，…，n）

其中第③个特点是因为：若将B_i与B_j相比的结果记为b_ij，反之B_j与B_i相比较的结果则为b_ji=l/b_ij，即转置对应的元素互成反比。

具有上述几个特点的矩阵称为正互反矩阵。可以证明一个n阶的判断矩阵只有n（n-1）/2个元素需要确定。(www.daowen.com)

3.层次单排序

所谓层次单排序是指，根据判断矩阵计算对于上一层某一因素而言，本层次与之有联系的因素的重要性次序的权值。它是本层次所有因素相对上一层次而言的重要性进行排序的基础。

层次单排序可以归结为计算判断矩阵的特征根和特征向量问题，即对判断矩阵A，计算满足

AW=λ_maxW

的特征根与特征向量，式中λ_max为A的最大特征根，W为对应于λ_max的正规化特征向量，W的分量W_iW_i为相应因素单排序的权值。首先，求出判断矩阵的最大特征值λ_max，然后计算其相对应的特征向量W；再对W作归一化处理，即得到权重向量。

为了检验矩阵的一致性，需要计算它的一致性指标CI

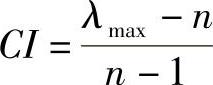
当判断矩阵具有完全一致性时，CI=0。为了检验判断矩阵是否具有满意的一致性，需要将其与平均随机一致性指标RI进行比较，得到随机一致性比例CR=CI/RI。当CR＜0.10时，判断矩阵具有满意的一致性。

4.层次总排序

层次总排序就是基于层次单排序得到的结果计算组合权重，然后通过比较各要素组合权重的大小，得到要素的相对重要顺序，依此确定对备选方案的评价，见表27-4。

表27-4 层次总排序

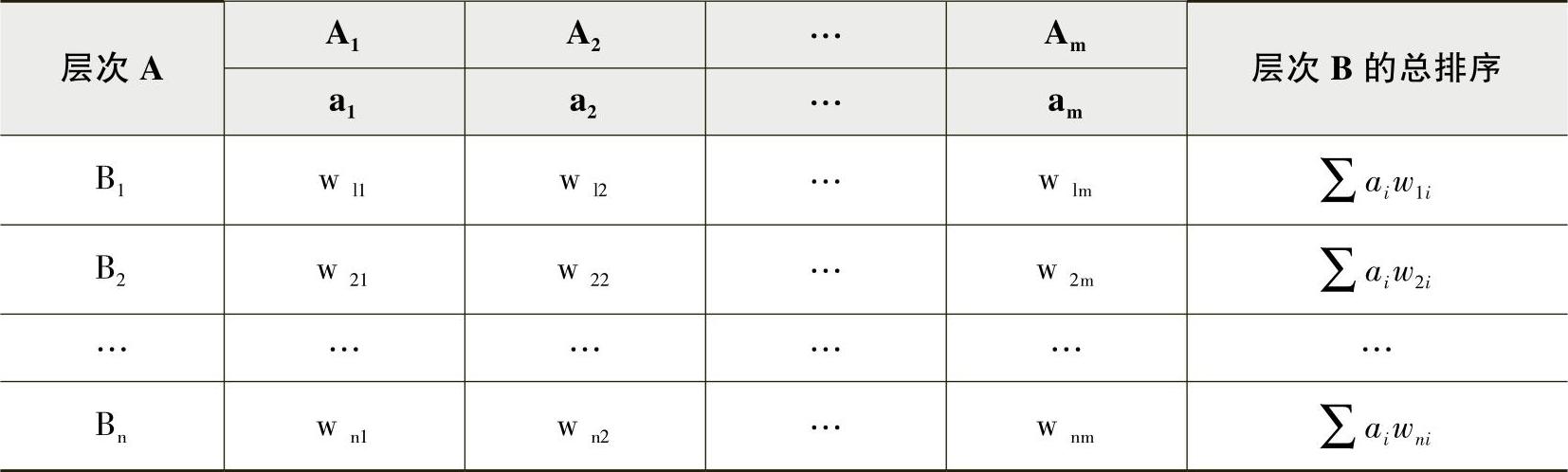
对于图27-1所示的层次结构模型，假定上一层次所有因素A₁，A₂，…，A_m的总排序已完成，得到的权值分别为a₁，a₂，…，a_m，与a_i对应的本层次因素B₁，B₂，…，Bn单排序的结果为w_1i，w_2i，…，w_ni。层次总排序如表27-4所示。其中∑为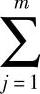的简写。

显然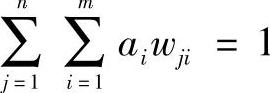，即层次总排序仍然是归一化正规向量。

5.一致性检验

为评价层次总排序的计算结果的一致性如何，需要计算与单排序类似的检验值。

CI为层次总排序完全一致性指标，其表达式为：

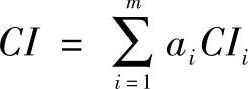
式中CI_i为与a_i对应的B层次判断矩阵的一致性指标。

RI为层次总排序的平均随机一致性指标，其表达式为：

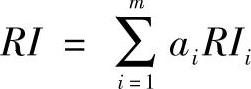
式中RI_i为与a_i对应的B层次判断矩阵的平均随机一致性指标。

CR为层次总排序随机一致性比例，其表达式为：

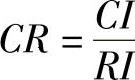
通常CR≤0.10，则认为一致性达到要求，否则必须调整判断矩阵中的元素。