1.关联矩阵法

关联矩阵法是一种常见的综合评价方法。它适用于各备选方案之间不存在互相影响的情况。关联矩阵见表27-1。

表27-1 关联矩阵

其中：

A₁，A₂，…，A_m为某评价对象的m个备选方案。

X₁，X₂，…，X_n为评价备选方案的n个评价指标。

W₁，W₂，…，W_n为n个评价指标的权重。

V_i1，V_i2，…，V_in为第i个备选方案A_i关于指标X_j（j=1，2，…，n）的价值评定值。

第i个备选方案的综合评价值为：

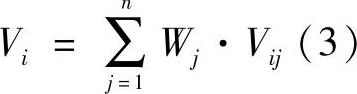
由上式可知，计算备选方案的综合评价值，必须知道各评价指标的权重系数W_j以及备选方案关于各评价指标的价值评定值V_ij。在实际评价过程中，备选方案在各评价指标下的价值评定值往往具有不同的量纲，因而想要得到备选方案的综合评价值，必须先对评价值做无量纲化处理。下面几种方法都是常用的无量纲化处理方法：

（1）目标打分法。这种方法的具体步骤是，先把评价项目即评价指标按照报告期实现程度分为若干等级，分别制定出各等级的评分标准；然后根据各评价对象对各项目的实现程度，按评分标准打分；最后进行汇总和规范化处理，求得各评价对象的综合评价值。

（2）线性差值法。这种方法是将某个指标下的最优值定为10分，最差值定为1分，连接两点得到一直线，其他数值可代入直线方程计算求得评价值。

（3）判断矩阵法。这种方法是将备选方案在各指标下的评定值通过转换，形成判断矩阵；然后计算判断矩阵的特征向量，并规范化处理，求得指标评定值的标准化结果。需要说明的是，对于已量化的指标评定值可直接构造判断矩阵，如果指标评价值要求越小越好，可采用其评定值的倒数来构造判断矩阵。

2.相关树法

相关树法作为一种对复杂问题的决策和评价方法，其应用十分广泛。它是从希望的目标和为实现目标应采取的方案两个方面出发来分析问题的，并把各种因素的关系在树状结构上加以表示，这种树形结构就称为相关树。根据相关树可以定量地对系统进行评价，即评价相关树的各水平层次中各因素的重要性以及各项目在整体系统中所处的地位。当备选方案很多，因素复杂且相互交叉时，采用这种方法非常有效。这种方法的步骤如下：

（1）在相关树的各层次上，设定各评价因素（方案）的评价基准（评价指标），分别记为α，β，…，ν（评价基准之间应尽可能独立，避免相互交叉或包含）。

（2）确定各评价基准的权重q_α，q_β，…，q_ν，且使q_α+q_β+…+q_ν=1（归一化处理）。(www.daowen.com)

（3）在各评价基础上，分别确定各因素的相对重要度。

（4）将评价基准k的权重qk乘以各因素在该评价基准上的权值，然后对所有基准求和，再进行归一化处理。

（5）在完成各层次因素的评价后，将与某因素有关联的上一层次的权重与本层次的权重连乘，即可得到某项目在整个系统中的重要度。

3.模糊综合评价法

模糊综合评价法是运用模糊集合理论对某一对象进行综合评价的一种方法。在现实生活中要想精确地描述某一评价目标，往往极为困难，例如，“把企业办得更好”“提高服务质量”等，这些评价标准往往是由决策者主观确定的。因此有必要建立一定的评价函数来衡量这种模糊目标。而评价函数可由模糊集合理论得到。

模糊综合评价方法包括以下内容：

（1）因素集U——类似于评价指标集。对某一事物进行评价，若评价的指标因素（着眼点）为n个，分别记为u₁，u₂，u₃，…，u_n，则这n个评价因素便构成了一个评价因素的有限集合U={u₁，u₂，u₃，…，u_n}。

（2）评价集V。若根据实际需要将评语划分为m个等级，分别记为v₁，v₂，v₃，…，v_m，则又构成了一个评语的有限集合V={v₁，v₂，v₃，…，v_m}。如四级评语制，评语级V={优秀、良好、及格、不及格}。

（3）确定权重集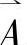。在实际评价工作中，各个评价因素的重要程度往往是不相同的，考虑到这个客观存在的事实，评价因素集合实际上是因素集合U这一论域上的一个模糊集合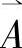，通常也可用一个模糊向量来表示。

（4）专家进行评价打分。若我们只着眼于一个因素来评定该教材，采用“民意测验”的办法，结果是16%的人说它“很好”，42%的人说它“好”，39%的人说它“一般”，3%的人说它“差”，则这个结果可用模糊集合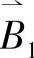来描述。

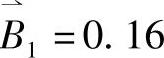/很好+0.42/好+0.39/一般+0.03/差

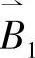也可简记为向量的形式

评价结果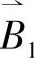是评语集合V这一论域上的模糊子集。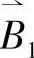就是对被评对象所做的单因素评价。

（5）建立评价矩阵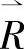。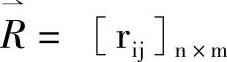为从U到V的一个模糊关系，其元素r_ij表示从第i个因素着眼，做出第j种评语的可能程度，也有人将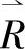称为“隶属度矩阵”。

（6）进行综合评价。一个模糊综合评价问题，就是将评价因素集合U这一论域上的一个模糊集合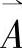经过模糊关系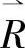变换为评语集合V这一论域上的一个模糊集合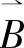，即

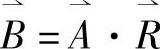
（7）得到具有可比性的综合评价结果，并选择较优方案。