为了探索经济改革和人力资本对经济增长的长期性影响，本部分通过一个协整分析来检验经济增长的长期均衡条件并试图依此来追踪这些改革的影响路径。

前面提到，进行协整检验的前提是两个或两个以上的不平稳时间序列变量通过处理后是同阶单整的，进而得出的长期均衡等式才是有意义的。根据方程4-3的结构形式，本部分将各变量都处理成了对数形式以更好地进行分析。检查序列平稳性的标准方法是单位根检验，ADF检验可以用来检验含有高阶序列相关的序列的单位根，这克服了DF检验只有当序列为AR(1)时才有效的缺陷。具体来说，ADF检验通过对检验方程的参数进行改进从而避免了原序列若存在高阶滞后相关将会破坏随即扰动项εt为白噪声的假设，假定序列yt服从AR(p)的过程，那么改进后的检验方程可以表示为:

这里的yt是非平稳的时间序列变量，它随着时间的变动而变动，xt是外生的变量，可以被理解为一个常数或者同时含有常数和时间变化趋势项，α和β是需要被估计的参数，εt是白噪声。

原假设和备选假设分别为:H0∶α＝0；H1∶α＜0，分别表示方程存在单位根和不存在单位根(即序列是平稳的)。如果序列存在单位根(即符合原假设)，那么对参数α的估计值进行显著性检验的t统计量将不会服从常规的t分布。

根据1993—2011年间各变量的原数据计算得出的ADF统计值与显著性具体如表4-5所示。

表4-5　对原序列的ADF单位根检验

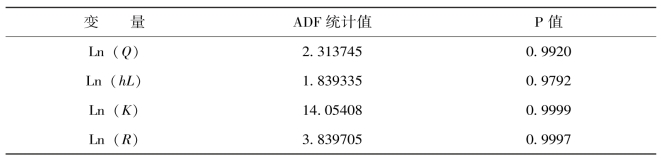
从表4-5中我们可以看到，在1%的显著性水平上所有四个变量都不能拒绝原假设，即都是非平稳的序列。为了确定单整的最后阶数，对一阶差分后的序列继续进行ADF检验，表4-6展示出检验的结果。

表4-6　对原序列一阶差分后的ADF单位根检验

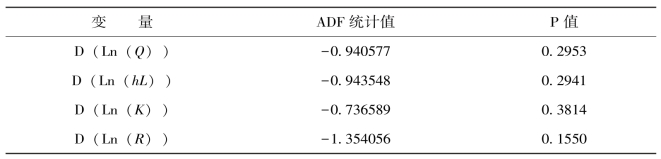
可以看到一阶差分后的序列在1%的显著性水平上依旧是非平稳的，继续进行二阶差分的ADF检验，结果如表4-7所示。

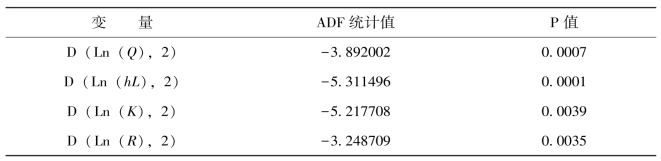
表4-7　对原序列二阶差分后的ADF单位根检验

(www.daowen.com)

通过以上的结果我们可以看出，至少在99%的置信水平上拒绝原假设，即二阶差分后的各个原序列是不存在单位根的。也就是说非平稳序列yt经过二阶差分平稳，所以是二阶单整序列。这样我们就可以进行接下来的协整分析，第一步就是确定VAR(p)模型的滞后阶数p，本部分通过似然比(LR)检验方法来确定这一数值。

LR检验从最大的阶数开始，检验的原假设为:在滞后阶数为j时，系数矩阵的元素皆为0；备选假设则是系数矩阵至少一个元素不为0。LR统计量如下:

这里的T是指观测的总样本数，C是可选择的一个方程的参数个数，等于内生变量个数和阶数之积与外生变量个数二者之和，Aj-1和Aj分别表示滞后阶数为j-1和j的VAR模型的残差协方差矩阵的估计。从最大阶数开始，比较LR统计量与5%水平下的临界值，如果时，拒绝原假设，表示统计量显著，此时表示增加滞后值能够显著增大极大似然的估计值；反之，每次减少一个滞后数，直到接受原假设。根据此方法，我们得出滞后数为一阶可以较好地反映中国改革后数据的变化过程。

表4-8和表4-9是对方程4-3四个变量进行Johanson协整检验的结果输出，从表4-8的结果我们可以看到，无论是跟踪特征值检验还是最大特征值检验都表明四个时间序列只存在一种协整关系。表4-9则列出了协整变量间的系数，这些系数均在5%的显著性水平上显著，它们使得四个变量在长期中趋于均衡。

表4-8　协整关系个数检验结果

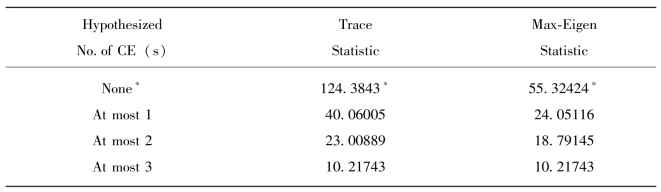
注:*表示在5%的显著性水平上拒绝原假设。

表4-9　标准化前后的相关系数

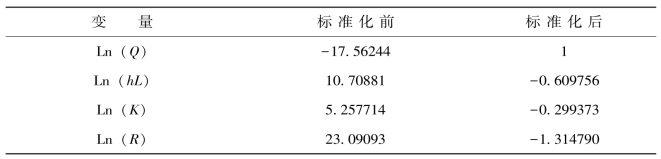
注:所有标准化前的相关系数均在5%的显著性水平上显著。

根据上表中的变量间的系数，我们得到了一个模拟长期过程的等式关系:

从经济学意义上，我们可以将等式4-6看作是潜在的经济长期增长函数。首先我们可以看到，以人力资本衡量的广义劳动力对经济的长期增长具有显著的促进作用。中国是世界上劳动力资源最丰富的国家，在90年代初就有6亿多劳动力，而与此同时中国无论是在教育水平(以高校入学率和平均受教育年限、识字率等指标衡量)上还是预期寿命上，与发达国家相比均是处于比较低的水平，这说明中国的人力资本状况具有很大的发展潜力或者说提升空间，即通过人力资本的积累而提高的经济总产出将会远高于其稀缺要素资本所带来的产出，这将会成为中国未来经济增长的重要动力之一。式4-6同时还揭示了改革对经济增长的巨大作用。由于体制、历史等方面的原因，我国的社会生产力长期受到束缚，生产效率低下，经济结构僵化严重脱离市场和人民群众的实际需求，国民经济缺乏活力与生机，而以市场化改革、对外贸易改革、国有企业改革等为代表的改革措施的实施，极大地解放和促进了生产力的发展，在极大促进经济增长的同时也有力地促进了社会方方面面的长足发展。由于改革的巨大作用，有必要进行进一步的分析。